基于快速傅里叶变换的谐波和间谐波检测修正算法

黄 峰，杨洪耕

（四川大学电气信息学院，成都 610065）

0 引言

目前快速傅里叶变换 （Fast Fourier Transform，FFT）已经应用于谐波的频谱分析[1-6]，但是随着非线性元件的广泛应用，电力系统中不仅有谐波，还有间谐波[7-8]，且电力系统的频率也不是保持固定不变，利用FFT算法检测谐波时存在频谱泄露和栅栏现象，导致检测出的谐波的频率、幅值和相位存在较大误差，不能满足检测的精度要求。

将离散傅里叶变换（DFT）应用于谐波及间谐波检测，计算效率高，且分辨率较高，可以用于处理噪声信号[9-12]。采用加窗[13]和插值[14-15]技术可以减少频谱泄露，提高分辨率，但是不能从根本上杜绝频谱泄露。多项式插值技术利用DFT，将采样信号从时域转变到频域，在频域利用插值技术可以算出正确的基波频率[16]。该方法计算速度快，分辨精度高，且能有效地改良频谱泄露的影响。

本文提出一种基于FFT的修正算法来检查信号中的谐波和间谐波，能有效减少信号检测中基波频率变化的影响，克服较低的频率分辨率。该算法通过对FFT算法做简单变换，减少了频谱泄露误差，利用频域插值算法对谐波和间谐波分开进行分析检测，抑制了谐波和间谐波之间的相互干扰。仿真结果表明，本文提出的电力系统谐波和间谐波检测方法具有检测精度高和响应速度快等特点。

1 检测谐波和间谐波的修正算法

假设有一信号v（t），对其采样：

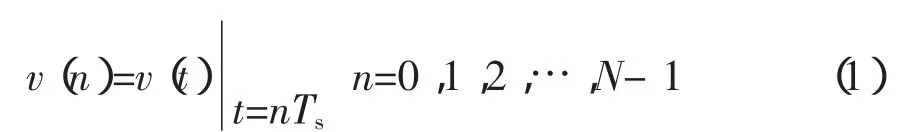
式中，Ts=1/fs，为采样间隔时间，fs为采样频率；N为每个周期采样点数。

一般采样信号可以分为2个部分：

式中，vh（n）为基波和谐波分量；vi（n）为间谐波分量。

1.1 频谱泄露和栅栏效应

FFT应用于信号处理时，由于时域波形某小段时间被截断会引起频谱泄露。当采样频率和周期一定时，基频频率波动会加剧频谱泄露，从而导致检测结果存在较大误差。

为了减少频谱泄露的影响，可以选取合适的采样频率，使得时域的采样数据是基波周期的整数倍，即：

式中，Ns为每个基波周期的采样点数；fs为采样频率；fd为基波频率，可通过频域插值算法求取。

此外，在非同步采样时，由于实际信号的各次谐波分量频谱并不能准确落在频率分辨点上，而是落在两个频率分布点之间，因此，通过FFT并不能得到各次谐波分量的准确值，而只能以临近频率分辨点的值来近似代替，这就是通常所说的栅栏效应。

为了减少栅栏效应的影响，可以选取合适的频率分辨率。如果采样频率和采样点数相等，此时频率分辨率为1 Hz，即：

式中，fr为频率分辨率；N为采样点数。

然而，谐波频率过高，采样数据随着增多，此时谐波检测的实时性将会降低。为了防止栅栏效应，可以采用频域插值算法估计间谐波，且不存在频率分辨率的问题。

1.2 谐波和间谐波频谱的相互干扰

FFT是对信号离散时间傅里叶变换（DTFT）频域采样[17-18]。当信号中只含谐波成分且同步采样时，FFT所得谐波参数是完全准确的，不存在相互干扰。当信号中存在间谐波时，由于此时采样对间谐波而言是非同步的，其DTFT在谐波对应的离散频点上不为0，此时通过FFT检测到的谐波参数就会有误差。根据时域频域的相互关系，可以通过加长采样窗口的长度使各分量频谱接近脉冲信号，以减小间谐波对谐波的干扰，但是实时性将会变差。

谐波对间谐波频谱存在干扰，由于FFT谐波频谱在除了整数倍基频点外的其他频点上为0，因此，以5 Hz为频率分辨率的各个离散频谱（去除谐波对应频点）为间谐波单独作用的结果。当谐波与间谐波的频率差大于半个主瓣宽度时（对应矩形窗为10 Hz），谐波在FFT结果上对间谐波主瓣内谱线没有影响，间谐波检测的误差主要是由栅栏效应和各个间谐波之间的频谱干扰所引起。但当所加窗的主瓣较宽时，或间谐波的频率与某一谐波频率之差小于主瓣宽度时，谐波在FFT结果上就会对间谐波产生影响。

施工建设阶段资金补偿并不适用于各种施工建设的项目，而是适用于建设需要资金较大的项目，通常这种项目的范围很小，共分为两种：一是项目付出的成本与项目的运营效率联系十分密切的项目，通常表现为经营性的项目；二是建设的永久性设施，通常表现为政府为了提高居民的生活品质而出资建设的基础性设施。在项目施工阶段，政府会将建成的部分项目交与社会企业经营，并签订相应的合同，使企业能够获得相应的经济效益，待项目正式运营以后，政府会对资产形式进行调整，以此来获取收益。

1.3 谐波和间谐波检测过程

本文提出检测谐波和间谐波的基本原理和主要步骤如下。

1）以预定的采样频率fs和采样间隔Ts对待检测信号v（t）在时域进行采样。

2）运用频域插值算法[16]算出正确的基波频率f′s。

3）运用频域插值算法求出待检测信号中的基波和谐波成分v′h（n）。

4）将步骤3）中检测出的基波和谐波分量v′h（n）从采样信号v′（n）中去掉，即得到间谐波分量，即：

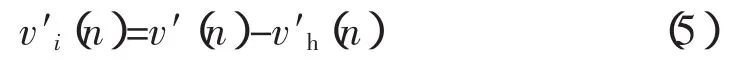
5）利用频域插值算法算出间谐波分量v′i（n）中幅值最大的间谐波分量的幅值、相位和频率。

6）将v′i（n）中的幅值最大的间谐波分量去除。

2 仿真过程及结果

为了验证修正算法检测谐波和间谐波的实用性，仿真信号和实际信号将分别在Matlab7.0中进行试验，并与其他算法进行比较分析。

2.1 仿真信号

设含有多个谐波和间谐波分量的采样信号

电力系统中基波频率一般并不是保持50 Hz固定不变的，而是在一定范围内波动。GB/T 15945-1995规定电力系统的频率偏差范围为±0.2～±0.5 Hz。现考虑非同步采样下信号基波频率为f=50.5 Hz,更加贴近实际电网频率波动的情况。现对式（6）所示信号做仿真分析，信号具体参数如表1所示，FFT变换的频谱图如图1所示。

表1 仿真信号参数

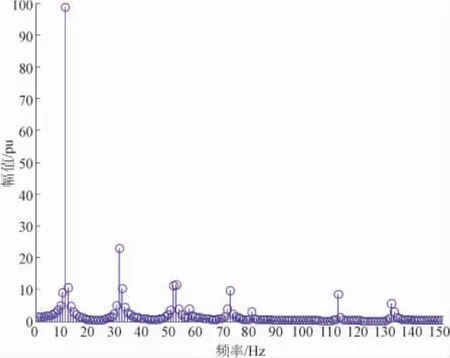
图1 基于FFT的检测信号频谱图

采样频率为10 kHz，采样窗口长度为M=10个基波周期。分别采用3种方法对谐波和间谐波参数进行计算,方法1为传统FFT方法，方法2为频域插值法，方法3为本文修正算法。谐波和间谐波的计算结果及相对误差如表2和表3所示。由表2和表3知，检测出的基波频率（50.5 Hz）偏离额定基波频率（50.0 Hz）0.5 Hz。由检测结果可知，当电力系统基波频率波动时，随着谐波次数的增大，频谱泄露和栅栏效应影响增大，FFT所得计算结果误差越来越大，导致检测结果出现较大误差，尤其是相位的计算结果已完全不可信。方法2在信号不含间谐波时能较准确地测量出谐波分量，当信号中含有间谐波时，由于谐波和间谐波之间的相互干扰，且谐波在信号中含量很大，对邻近的间谐波频谱有较大影响，插值算法计算间谐波时结果有较大误差。由表2和表3知：5次谐波对5.5次间谐波的检测存在较大的影响，导致检测间谐波时幅值和相位结果均存在较大的误差。本文通过对算法修正，先检测基波和谐波部分，然后消除谐波对间谐波频谱的影响，计算得到的间谐波和谐波参数精度较高，且计算量很小，由只含间谐波频谱的图2可以清晰看出，间谐波在250～300 Hz以及400 Hz附近。修正算法在系统频率波动和信号中含有间谐波的情况下，都能检测出较好的结果，而且修正算法的计算量与FFT和插值算法相比，并没有增加，检测精度却优于FFT和插值算法。

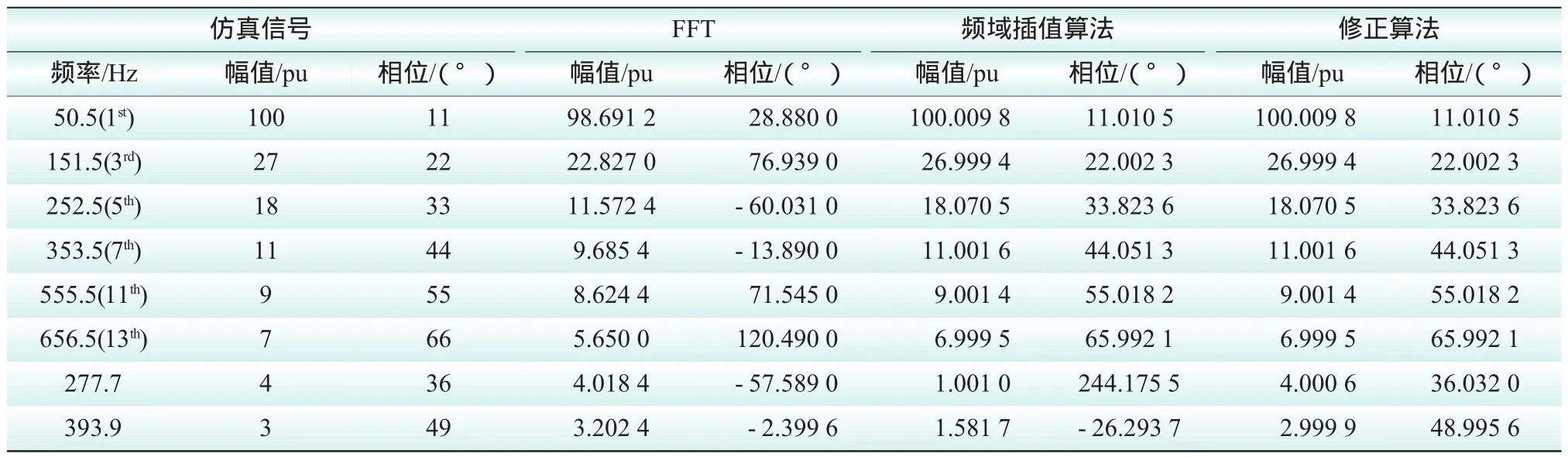
表2 仿真信号参数及结果对比

表3 仿真信号误差对比

2.2 实际信号

根据电弧炉启动过程中实测电流数据进行频谱分析，采用MATLAB分析计算，验证修正算法检测实际信号中间谐波频率、幅值和相位的准确性。

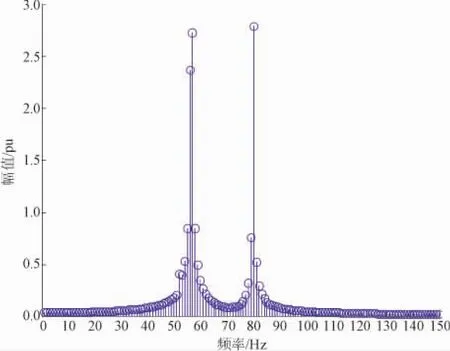
图2 只含间谐波的信号频谱图

信号采样频率为5 kHz,，采样窗口长度为M=10个基波周期，采样点数为1000，用修正算法对实际信号进行仿真分析，结果如表4所示。基波频率50.0162 Hz,符合实际情况，3次谐波和9次谐波含量较小，5次谐波和7次谐波含量较大，间谐波在基波附近，且含量很小，不去除基波成分时很难检测到。

表4 电弧炉启动电流谐波间谐波检测结果

由图3和图4，根据修正算法检测到的结果重构的波形和采样波形基本相同，验证了检测结果的准确性。

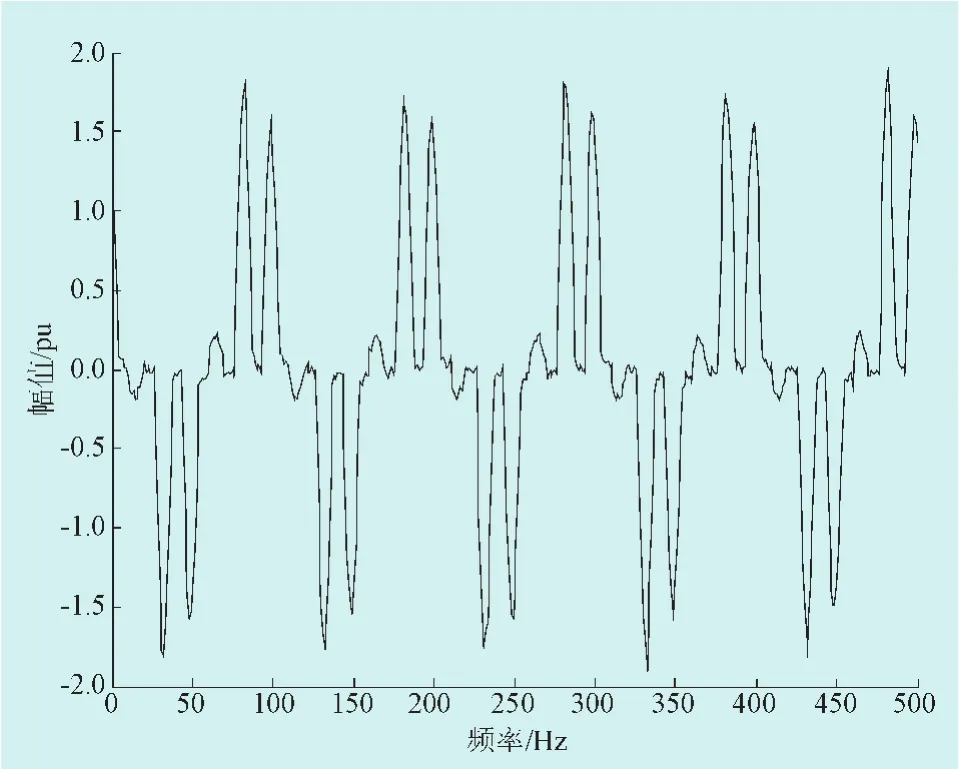
图3 采样波形

图4 根据检测结果重构波形

图5和图6分别为FFT和修正算法检测时的信号频谱分布图。图5中由于基波和谐波对间谐波的干扰，只能看到基波和谐波频谱，间谐波只有在滤除了基波和谐波成分后可以看到，如图6所示，可以清晰看出间谐波在30～35 Hz以及65～70 Hz附近，和检测结果一致，能够比较准确地检测出间谐波。

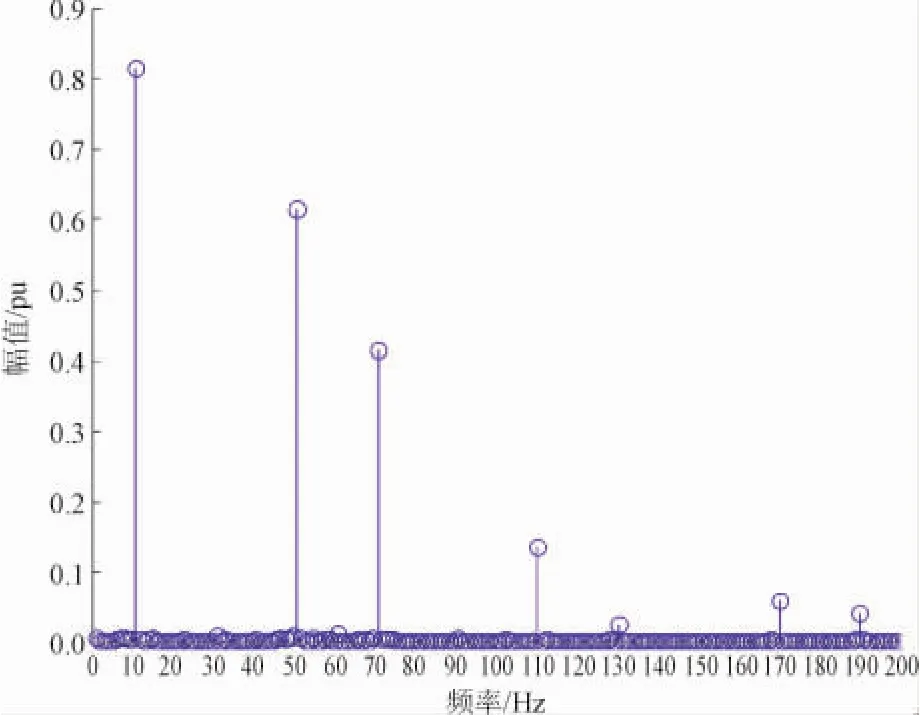
图5 含谐波和基波的信号频谱图

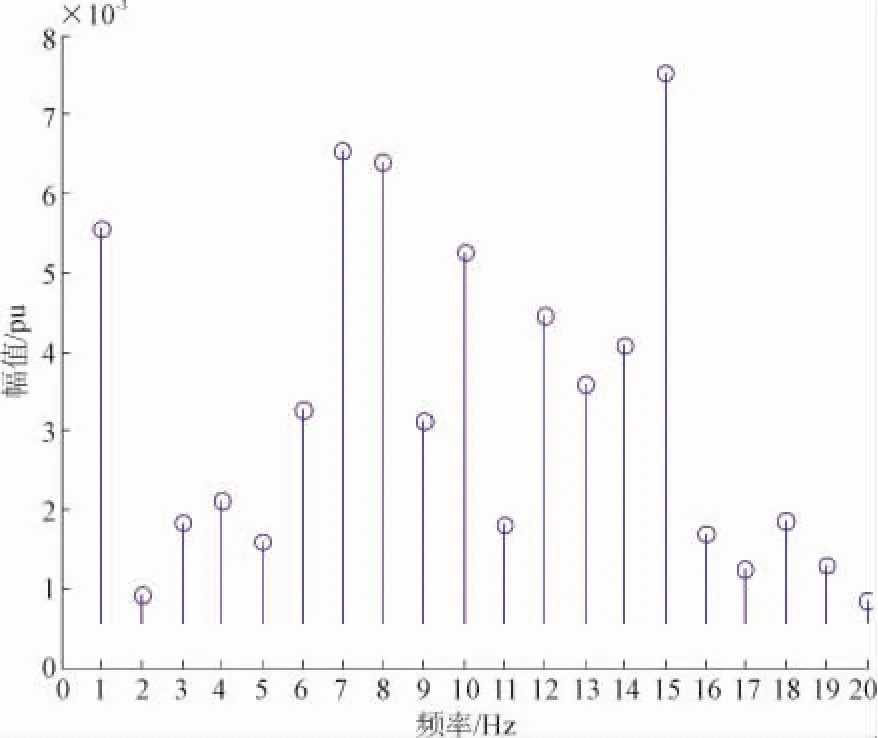
图6 去除基波和谐波部分的信号频谱图

3 结论

1）非同步采样时，FFT对谐波计算存在较大误差，且谐波频谱和间谐波频谱之间存在相互干扰。

2）频域插值方法能准确计算谐波的参数，但对基波和谐波附近间谐波频谱计算存在较大误差。

3）本文先利用频率插值方法算出准确的基波和谐波成分,然后在时域去掉原信号中检测到的基波和谐波成分,大大抑制了基波和谐波对间谐波检测的干扰，提高了间谐波的检测精度，计算简单快速。仿真结果表明了本文方法的准确性。

[1] Santamaria-Caballero I,Pantaleon-Prieto C J,Ibanez-Diaz J，et al.Improved Procedures for Estimating Amplitudes and Phases of Harmonics with Application to Vibration Analysis[J].IEEE Transactions on Instrumentation and Mesurement,1998,47(1):209-2144.

[2] 潘文,钱俞寿,周鹗.基于加窗差值FFT的电力谐波测量理论(I)窗函数研究[J].电工技术学报,1994,9(1):50-54.

[3] 潘文,钱俞寿,周鹗.基于加窗差值FFT的电力谐波测量理论(II)双插值FFT理论[J].电工技术学报,1994,9(2):53-56.

[4] 张伏生,耿中行,葛耀中.电力系统谐波分析的高精度FFT算法[J].中国电机工程学报,1999,19(3):63-66.

[5] 赵文春,马伟明,胡安.电机测试中谐波分析的高精度FFT算法[J].中国电机工程学报，2001,21(12):83-87.

[6] 郑恩让,杨润贤,高森.关于电力系统FFT谐波检测存在问题的研究[J].继电器,2006,34(18):52-57.

[7] 祁才君,王小海.基于插值FFT算法的间谐波参数估计[J].电工技术学报,2003,18(3):92-95.

[8] 钱昊,赵荣祥.基于插值FFT算法的间谐波分析[J].中国电机工程学报,2005,25(21):87-91.

[9] 万康鸿,别瑞那.三次谐波电流闭锁式变压器过激磁保护分析[J].电网与清洁能源,2010,26(3):25-30.

[10] 林建钦,杜永宏.电力系统谐波危害及防止对策[J].电网与清洁能源,2009,25(2):28-31.

[11] 李世博.电力系统谐波有效检测与抑制[J].电网与清洁能源,2009,25(7):39-42.

[12] 褚优群,彭晨光,刘连光.地磁感应电流在直流输电系统引发的谐波不稳定分析[J].电网与清洁能源,2009,25(9):11-15.

[13] 孙红伟,李梅,袁健华,等.用于电力系统谐波分析的加窗FFT算法研究[J].高电压技术,2004,30(8):52-55.

[14] 庞浩，李东霞，俎云霄，等.应用FFT进行电力系统谐波分析的改进算法[J].中国电机工程学报,2003,23(6):50-54.

[15] 黄方能,黄成军,陈陈,等.高精度插值FFT谐波分析[J].中国电机工程学报,2007,27(9):40-42.

[16] Agrez D.Weighted Multipoint Interpolated DFT to Improve Amplitude Estimation of Multifrequency Sagnal[J].IEEE Transactions on Instrumentation and Mesurement,2002,51(2):287-292.

[17] 布赖母.快速傅立叶变换[M].柳群，译.上海:上海科学技术出版社,1979.

[18] 程佩青.数字信号处理教程[M].北京:清华大学出版社,2001.