基于启发式函数蚁群算法的VRP优化研究
郑小雪
(福建农林大学 交通学院,福建 福州 350002)
物流配送运输,一般是指配送中心按照不同客户多频度、小批量的订货要求进行组织配送,即根据货物量进行车辆的分配和配送线路的生成,也就是研究车辆的路径问题。由于从事城市配送汽车货运工作条件复杂,不仅货运点多、货物种类繁多、道路网复杂,而且运输服务地区内运输网点分布不均匀。因此,如何应用现代数学方法及计算机快速求解路线优化方案,是国内外专家学者普遍探索的重要课题。
1 VRP问题描述及分类
从配送中心 (物流据点) 用多辆车向多个需求点 (客户) 送货,每个需求点的位置和需求量为已知,每辆车的载重量一定,要求合理安排车辆路线,达到一定的目标 (如路程最短、费用最少、时间尽量少、使用车辆尽量少等) 即为VRP问题[1]。并满足以下条件:每条配送路径上各需求点的需求量之和,不超过车辆载重量;每条配送路径的长度不超过车辆一次配送的最大行驶距离;每个需求点必须满足,且只能有一辆车送货;每辆车均从中心出发,完成任务后又全部回到中心。
根据VRP问题的条件可分为以下分类:
(1)按照运输任务分为纯装问题、纯卸问题以及装卸混合问题。
(2)按车辆载货状况分满载问题和非满载问题。
(3)按照车辆类型分为单车型问题和多车型问题。
(4)按照车辆是否返回配送中心车场,划分为车辆开放问题和车辆封闭问题。
(5)按照优化的目标可分为单目标优化问题和多目标优化问题。
(6)按照有无时间要求可分为有时间窗问题和无时间窗问题。
实际中的车辆优化调度问题可能是以上分类中的一种或几种的综合。目前国内外用于解决该问题的现代数学方法,主要有以下几类[1]:精确优化方法、启发方法、模拟方法、交互优化法。
2 VRP问题的数学模型
VRP问题在现实的物流系统中可由服务区、仓库、分布在服务区内的服务点组成。要把经典的VRP问题抽象成一个数学模型,需要设定一些前提:只有一个仓库,所有车辆从这里装载货物出发,运送完货物返回仓库;所有的车辆能力都是一样的;每一个服务点只能由一辆车提供服务[2]。
设配送中心需向L个客户送货,每个客户的需求量是g,每辆车的载重量是q,cij表示从i点到j点的运输成本,其含义可以是距离、费用、时间等,设配送中心编码为0,客户编码为1,2,…,L,数学模型如下。

建立数学模型:
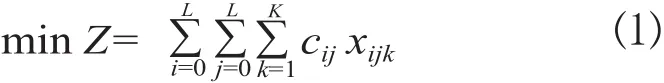

其中:式⑴保证了总成本Z最小;式⑵为车辆的载重量约束;式⑶保证了每个客户点的运输任务仅由一辆车来完成,而所有的运输任务则由K辆车共同完成;式⑷和式⑸保证每个客户能且只能被一辆车服务一次。
3 蚁群算法在求解VRP中的应用
3.1 蚂蚁的转移策略
蚂蚁的转移策略是蚁群算法的重要组成部分,是蚂蚁构造路径的过程,它在很大程度上决定了算法的性能。在求解TSP (旅行者问题) 时,由于每只蚂蚁需要遍历所有的结点,因此,初始状态下,蚂蚁可以位于任意结点,且在蚂蚁转移过程中,该只蚂蚁没有经过的所有结点,均可作为转移目标。而在求解VRP时,每只蚂蚁遍历路径应是:仅包含部分结点;包含且仅包含一次配送中心;路径必须满足车辆容量和行驶距离的限制。因此,在求解时,蚂蚁的初始位置与转移策略如下。
(1)所有蚂蚁的初始位置均为配送中心,每只蚂蚁在满足车辆容量和行驶距离限制的情况下,尽可能多地遍历结点,并最终返回配送中心。此时,每只蚂蚁的禁忌表中存放除配送中心以外的所有该蚂蚁已经遍历的结点。
(2)蚂蚁从任意结点出发,在完成一个包含配送中心,且满足车辆容量和行驶距离限制的回路后,结束遍历。此时,若某只蚂蚁的初始位置不是配送中心,则该蚂蚁的禁忌表中存放该蚂蚁已经遍历的所有结点,否则存放除配送中心以外的该蚂蚁已经遍历的所有结点。
3.2 可行解构造
当使用蚁群算法求解VRP时,每只蚂蚁只遍历部分结点,因此,当所有蚂蚁遍历完成时,从中选择满足车辆数限制的若干条蚂蚁遍历路径,即①这些蚂蚁恰好遍历了所有结点,且除配送中心外,每个结点仅被一只蚂蚁遍历;②这些蚂蚁遍历的路径覆盖了所有结点,但是除了配送中心以外,有的结点被多只蚂蚁遍历;③这些蚂蚁遍历的路径并没有覆盖所有的结点,其中①中的路径构成一个可行解,但是这种情况出现的概率极小,而②和③中的路径均不能构成可行解,这就需要进行可行解构造,即删除除配送中心外被多只蚂蚁遍历的结点和插入未被蚂蚁遍历的结点。
3.3 算法优化
通过“3.1”和“3.2”节的操作后,蚁群算法可用于求解VRP,但是算法的求解性能可能并不好。可以从以下几方面提高算法的求解性能。
(1)为每个结点引入K邻域以限制蚂蚁在选择转移目标时,只在距当前结点较近的结点中选择。但是可能存在一个结点的K邻域中的结点均处于一只蚂蚁的禁忌表中的情况,此时需要另外设计转移规则,以防止该只蚂蚁不能完成回路构造。
(2)在“3.2”节中,删除结点和插入结点时设计有利于算法收敛的规则。例如,删除结点可按节约最大的原则,即保留重复结点中的一个而删除其他所有重复结点,使删除后总路径长度减小最大;而插入结点可按增加最小的原则,即将在所有路径中均未出现的结点插入到一条路径的恰当位置,使插入后总路径长度增加最小,如果节点不惟一时,任选一结点。
(3)设计有利于算法收敛的信息素更新策略。信息素更新策略是决定蚁群算法收敛与否的重要因素,传统的信息素更新策略对所有蚂蚁遍历的路径均增加信息素,而实际上,有些蚂蚁遍历的路径对最优解根本没有贡献,这样导致传统的信息素更新策略不利于蚁群算法的收敛。在信息素更新时,为了防止边上信息素的过分悬殊会导致算法快速收敛于局部最优解,为此,可以将信息素量限制于特定的范围内,对信息素量大于上限的边,直接将该边上的信息素量置为上限,而对信息素量小于下限的边,直接将该边上的信息素量置为下限。
(4)启发函数的设计。设计更有利于信息素向存在于最优解中的边集中的启发函数,从而加速算法的收敛速度。
4 引入启发式函数
在蚁群算法的基础上,采用启发函数中的节约算法来提高算法的求解性能。节约算法属于启发式算法[3],它的基本思想是首先把各个客户单独与车场相连,构成n条“0→i→0”(i,j=1,2,…,n),计算连接后费用的节约值。
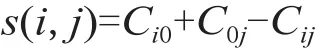
s(i,j) 越大,说明把客户i和客户j连接在一起时总费用节约值越多,因此应优先连接s(i,j) 值大的点i和j。基于这一原则,Clarke和Wright在1964年提出C-K节约算法。约定把只有一个客户的线路 (如“0→i→0”) 称为初始化线路,把包含两个或两个以上客户的线路 (如“0→...i→...→0”) 称为已构成线路。
4.1 转移规则细化
应用节约算法对蚁群算法进行细化,定义如下形式的蚂蚁转移概率[4]:
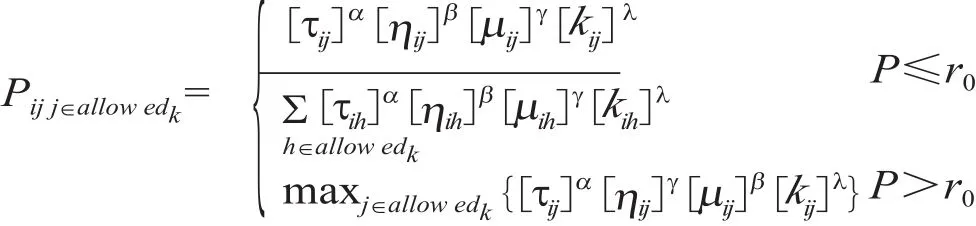
其中:τij代表边 (i,j) 上的信息素;ηij表示边 (i,j) 上的启发信息,常取边(i,j)长度的倒数,即ηij=1/dij。
应用节约算法,首先将各点单独与源点0相连,构成1条仅含一个点的线路;然后计算将点i与j在满足车辆载重量约束的基础上,连接在同一条线路上的费用节约值,即µij=di0+d0j-dij,显然,μij越大,收益越大,而选择结点vj的概率也就越大。μij的值需要作最大值和最小值限制,以免μij过大或过小而影响整个路径转移概率,如,当µij等于0时,转移概率为0,使得整个转移概率公式的其他影响因素失去意义。kij= (qi+qj) /Q是考虑车辆容量约束和车辆载重量利用率而引入的变量。α,β,λ,γ为权重参数。p是个随机数,取值在 (0,1) 区间内。r0为取值在 (0,1) 区间内的一个固定值。
4.2 信息素更新原则
采用全局更新规则,当所有蚂蚁走完所有的客户点,也就是完成一次遍历后,各路径上的信息素浓度要根据下式进行调整:
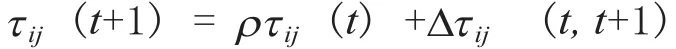
其中:ρ∈(0,1), (1−ρ)为信息素浓度的衰减系数,在本次遍历(t,t+1)时间段中信息素浓度的增量∆τij(t,t+1)表示为:
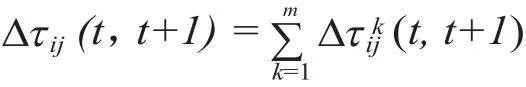

其中:∆τij表示蚂蚁k在本次遍历(t,t+1)时间段中留在路径(i,j)上的信息浓度,可用下式表示:
其中:Q为常数;Lk表示蚂蚁k在本次遍历中所走过的路径的长度。
4.3 Min-Max思想的引入
Min-Max蚁群系统(MMAS)是德国学者Stützle等提出的一种ACO算法的改进方案[5]。由于信息素随时间衰减因素的存在,在搜索陷入局部最优时,某段路径弧段的信息素相对其他路径弧段的信息素而言,在数量上占据绝对的优势,以至于引起算法过早地收敛。因此本算法对各路径弧段上的信息素,设定了最大和最小值的限制,从而避免了某段路径的信息素过大或过小。即τij(t)∈τmin,τmax) ,若τij>τmax,则τij=τmax;若τij<τmin,则τij=τmin。
4.4 算法步骤
步骤1:初始化各参数,输入基础数据,给定n个客户和每个客户的需求量,得出各需求点之间的距离,将m个蚂蚁平均分配到n个需求点,设定α、β、τij(0)车辆的额定载重量、最大循环次数Ncmax,计算出ηij,μij,kij的值并存放于相应的数组中,设置μij的最大值和最小值。
步骤2:将m个蚂蚁置于初始点(即配送中心),并将初始点置于当前解集中。
步骤3:对每只蚂蚁k,随机选择除初始点外的任意节点f,并将f置于当前解集中。
步骤4:对每只蚂蚁k,根据不同的p值选取相应的pijk,并根据剩余载重量选择下一结点j,将j置于当前解集中。
步骤5:重复步骤4,直到每只蚂蚁都访问了每一结点,受到车辆载重量的限制,每只蚂蚁将得到若干条由配送中心为起点的回路,每条回路就相当于一辆运输车所经过的路径。
步骤6:计算每只蚂蚁所走过的每条回路的路径长度,按照全局更新规则对各边的信息素进行更新。
步骤7:按照各蚂蚁所得到的可行解,得出最优解。
步骤8:依式τij(t+1) =ρτij(t) +∆τij(t,t+1) 进行信息素的全局更新。
步骤9:Nc=Nc+1,所有蚂蚁又回到初始位置,重复步骤2、3、4、5、6、7、8。每次迭代获得的最优解要与前面获得的解比较,若优于之前的解,则替换成当前最优解。
步骤10:直至Nc>Ncmax或者出现退化行为(即每次迭代找到的都是相同的解),则结束,输出最优路径及路径长度。否则转步骤2。
5 应用分析

表1 实例计算结果
本文参照文献[6]中的示例利用后的蚁群算法进行优化。设某物流中心有5台配送车辆,车辆的最大载重量均为8 t,一次配送的最大行驶距离均为50 km,需要向20个客户送货,物流中心的坐标为(14.5 km,13. 0 km),20个客户的坐标及其货物需求量。
第一次蚁群算法控制参数为:
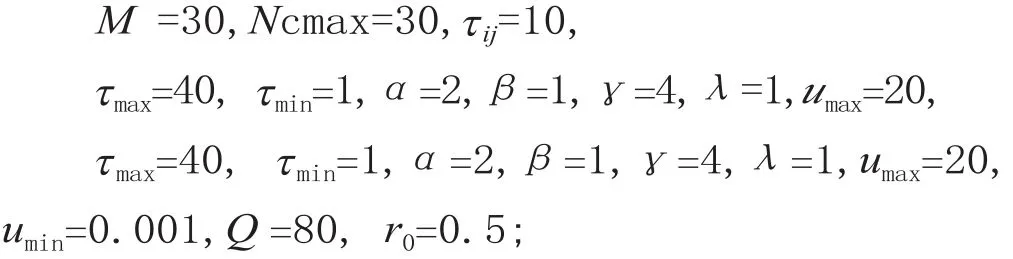
第二次蚁群算法控制参数为:M2=5,Ncmax2=30,τij2=1,τmax2=20,τmin2=1,α2=1,β2=5,Q2=50
程序运行10次,各次搜索结果如表1所示。
从表1中可以看出,采用本文的算法求解上述VRP均得到质量很高的解。其平均配送最小距离为111. 6 km,平均使用的车辆数为4辆。从计算效率来看,10次求解的平均程序运行时间为345.4ms。在10次求解中,平均与最优的差值比最优解多3.522%,可见,该算法在求解VRP可得到较好的结果。算法找到的最好解的配送距离为107.8 km,对应的4条配送路线为I:0→8→19→15→16→13→6→0;II:0→5→14→2→12→9→10→7→1→0;III:0→4→3→17→11→20→0; IV:0→18→0。文献[6]所设计的混合蚁群算法找到的最好解的配送距离为108.62 km,对应的4条配送路线为I: 0→5→14→2→12→9→10→7→1→0;II:0→8→19→15→16→13→6→0; III:0→18→20→11→17→3→0; IV: 0→4→0。相比之下,本算法能够找到更好的可行解,比其最优解少0.072 1%。
本文在传统蚁群算法的基础上,针对传统算法的不足,引入启发函数中的节约算法来对蚁群算法进行优化,并借鉴Min-Max的思想,使算法得到优化,通过实例证明了算法的优良性,能够较好地解决车辆路径问题,而且计算出来的结果更稳定。
[1] 彭 扬,伍 蓓. 物流系统优化与仿真[M]. 北京:中国物资出版社,2007.
[2] 黄天赦,叶春明. 基于混合粒子群算法的车辆路径优化问题研究[J]. 物流科技,2008 (9):26-27.
[3] 缪兴锋,秦明森. 物流运筹学方法[M]. 广州:华南理工大学出版社,2007.
[4] 王俊鸿,修桂华. 二次蚁群算法在运输调度问题中的应用[J]. 计算机应用与软件,2008 (7):71-73.
[5] Stützle T, HoosH. Improvements on the ant system:introducingMax-min ant system[A]. Proc. Int. Con.f ArtificialNeuralNetwork and GeneticAlgorithm,W ien:SpringerWerlag,1997.
[6] 李卓君. 混合蚁群算法求解物流配送路径问题[J]. 武汉理工大学学报,2006 (2):306-309.

