基于簇域的P2P信誉评估模型
王 铮,翁 涛
(重庆大学 计算机学院,重庆400044)
P2P网络是一个开放的、动态的网络,没有权威中心对这些节点进行管理,使P2P网络也受到如冒名、诋毁等各种形式的攻击行为,因此需要建立一种信任模型来遏制这些攻击行为。
不同拓扑的P2P网络环境有不同的信任解决策略。非结构式P2P网络中的信任模型,如Beth信任模型[1-3]、JØsang信任模型[4]等,都是通过泛洪方式迭代方式获得节点的全局信任度,但会带来大量的资源开销。在结构式 P2P网络中的信任模型利用 Chord、CAN和 Pastry等算法快速定位查询全局信任度,但对高度动态性的P2P网络,不具有信任模型规模的扩展性。因此,针对结构式P2P信任模型的信任计算开销大和非结构式P2P信任模型的网络规模不易扩展等缺点,本文以P2P电子商务为研究背景,设计了一种基于信任向量的混合结构式P2P网络信任模型(P2P-CRep)。利用混合结构式P2P网络存取信任向量存储的历史交易数据,利用信任的衰减性计算信誉度。通过仿真实验验证了P2P-CRep信誉模型的合理性和对恶意行为的防御能力。
1 P2P-CRep信誉管理模型
信誉是在特定的前提和时间下,基于其他实体对该实体以往信任的总结。
本文P2P-CRep信任模型的系统应用环境采用基于簇域的信誉管理系统。该系统拓扑结构融合了集中式P2P网络拓扑和结构化P2P网络拓扑的优点,提高了资源定位的效率,降低了网络消耗,同时增加了网络扩展性。
该系统模型由两层网络组成:索引网络层和簇域子网层,拓扑结构如图1所示。
索引网络层由性能较强的超级节点SP(Super Peer)构成,主要负责资源信息发布、索引、信任数据的存储和信誉评估。索引网络层在系统中是较为稳定的子网,因而采用结构化DHT P2P网络协议Chord协议[5]进行路由。
簇域子网层由若干普通节点CP(Common Peer)和一个备份节点BSP(BackupPeer)构成,CP节点根据自己的兴趣爱好加入不同的簇域,并与其他节点进行交易。BSP节点负责SP节点的数据备份,是SP的后备节点。为了便于网络扩展,簇域子网采用集中式P2P网络构成。

2 P2P-CRep信誉评估模型
在不同的应用背景环境下,信誉评估模型会有不同的设计要求,本文的P2P-CRep信誉评估模型是针对电子商务的应用环境设计的。
2.1 交易评价度的推理
在电子商务中,交易的因素呈现多样化和层次化,适合应用模糊数学的综合评估方法推理[6]。其流程如图2所示。

图2 模糊推理流程
由于电子商务交易记录中含有许多模糊量的交易指标,所以适合应用模糊逻辑推理规则推理交易评估因子。
假设在电子商务交易中的交易指标集合为:H={x1,x2,… ,xn,k1,k2,… ,kn},其 中 :X={x1,x2,… ,xn}为 模 糊 指标子集,如 After Service 等;K={k1,k2,…,kn}是精确指标子集,如Transaction Amount等。下面给出利用模糊推理规则对这些指标推理交易评估因子ξ的具体过程:
(1)为精确指标子集K中各项指标和交易评价度ξ,设定模糊评价集 V={v1,v2,…,vm};
(2)设定隶属度函数,将精确指标子集模糊化。为精确指标子集的评价集设定隶属度函数:U={Uk1,Uk2,…,Ukn},Ukn={uv1(x),uv2(x), … ,uvm(x)}, 根 据 最 大 隶 属 度 原 则 :max(uv1(x),uv2(x),…,uvm(x))确定精确指标所属的评价等级:kn=vm;
(3)利用交易指标集建立模糊逻辑推理规则库,并进行推理。针对交易指标集合H中各项交易指标对应的不同评价集vm,建立多条模糊逻辑推理规则,以此形成一个模糊推理规则库R。推理时,找到规则库R里满足所有推理条件的一条推理规则Rn,推导出相应的结论(交易评估因子);
(4)交易评估因子的解模糊化。经过模糊数学的综合评判推理,得到的交易评价度ξ是一个模糊评价值,为了引入信誉评估的精确计算,需要将模糊值转换为相应的精确值。本文采用加权平均法(WFM)[7-8]解模糊化,将交易评价度ξ解模糊化。
2.2 直接信任度的计算
每次交易结束后,节点将交易记录存储在自身节点上,并根据滑动窗口更新历史交易记录。计算此时对交易节点的本次直接信任度,并信誉代理更新之前的直接信任度。因此,直接信任计算可以分为以下几个步骤:
(1)本次直接信任度的计算
设某次交易后的滑动窗口Win内存储了节点i与节点j最近发生的k次交易记录,每次交易的时间、评价度和交易量分别为 TSk、ξk和 mk。 由滑动窗口 Win得到的本次直接信任度Tcurd(i,j)可按式(1)进行计算:

其中初始直接信任度为0.5,是信任与不信任的临界值,交易评价度的计算权重时间衰减因子μl和交易量ml确定。
(2)时间衰减因子的确定
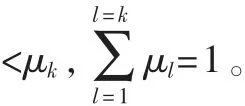

(3)直接信任度的更新
用户将本次直接信任度提交给本簇域的信誉代理,信誉代理节点要将用户节点的直接信任度更新。直接信任度更新的公式为:

其中直接信任度的初始值为0.5,即为信任和不信任的临界值。α为更新权重因子,由系统管理员确定。
信任度的提升越困难,信任度在商业上的价值就越大。本文通过系数调整控制信任度的收敛速度。由于直接信任度的初始值为0.5,所以系数调节的是直接信任度的变化值。直接信任度调节公式为:
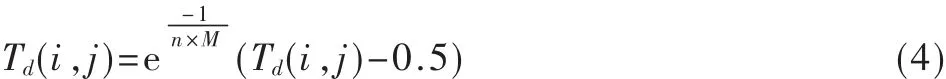
由式(4)可以看出,随着交易次数和交易量的增加,节点就越容易获取信任度,反之则否。此外,交易量M作为其中的一个因素,可以起到防止用户积累小交易信任度行骗的行为的作用。用户的交易量越小,直接信任度的提升越难。
2.3 推荐信誉度的计算
为了增加信誉评估的可靠性,信誉评估应收集并综合计算其他节点对评估客体节点的信任度。本文的推荐信誉度计算引入以下几个因素:推荐信任度、推荐可信度Cr(i,j)、推荐节点的数目Num和推荐阈值 λ。推荐信誉度的计算分为以下几个步骤:
(1)推荐可信度的计算
节点根据兴趣爱好加入不同的簇域,因此簇域差异间接表现为节点间兴趣爱好的差异。所以簇域和评估差异可以作为推荐可信度计算的两个重要因素。
①评估相似度
令推荐节点j和评估主体节点i对信誉评估客体节点 k的直接信任度分别为 Td(j,k)和 Td(i,k),所以推荐节点j与评估主体节点之间由于信誉评估误差而导致的推荐可信度为:
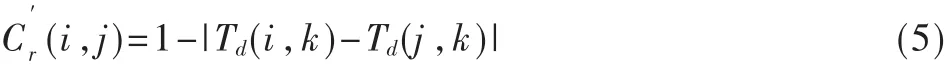
②簇域相似度
簇域可以根据兴趣爱好的细分生成子簇域。所以两个节点所在的簇域可以分为:节点i和节点j在相同的簇域,簇域相似度θj=1。节点j的簇域是节点i所在簇域的子簇域或有相同的父簇域。假设节点i和节点j的簇域路径长度为 k,则簇域相似度 θj=e-rk。节点j与节点i没有相同的簇域或父簇域,则簇域相似度θj=0。
综合评估相似度和簇相似度,推荐节点的推荐可信度为:

(2)推荐信誉度的计算
收集推荐节点的推荐信任度并计算相应推荐节点的推荐可信度后,便聚敛计算所有推荐节点对评估客体节点的推荐信誉度。推荐信誉度的计算公式为:

根据推荐可信度得到每一个推荐节点推荐信任度计算权重。为了防止电子商务中少数节点共谋的恶意行为,利用推荐节点数目Num来调节推荐信誉度的增长。推荐信誉度的调节计算公式为:

此外,为了降低热点节点的信誉评估复杂度,设置推荐信任度阈值λ>M,减少小交易量的节点推荐。
2.4 综合信誉度的计算
如何准确综合直接信任度和推荐信誉度计算信誉评估客体节点的最终信誉度,是信誉评估模型设计的一个关键问题。本文采用置信因子法计算综合信誉度,其计算公式为:

置信因子α、β是综合信誉度计算中的权重,表明对直接信任度和推荐信誉度的倚重程度。其值的确定主要根据以下两个因素:
综合所有推荐节点的推荐可信度,计算得到平均推荐可信度。根据平均推荐可信度,可以设置推荐信誉度的计算权重β。系统管理员根据需求对[0,1]进行推荐可信度区间划分,确定区间相对应的推荐信誉度置信因子β1的值,形成如表1的推荐置信因子表。

表1 推荐信誉度置信因子
(2)平均交易量M
综合所有推荐节点与评估客体节点交易量,计算得到平均值交易量。令评估主体节点与客体节点之间的交易量为M,则推荐信誉度的置信因子β为:
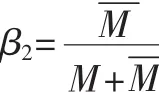
综合以上两个因素,便可确定置信因子:

3 信誉评估算法描述


4 模型性能分析及仿真实验
4.1 模型性能分析
为了分析基于簇域的信誉评估模型的性能,首先作如下假设:
(1)假设索引网络层中有M个SP节点,在该层中每次索引查询需要经过的跳数为h;
(2)假设电子商务中有N个CP节点,则平均每个SP节点为CP节点提供服务的节点数目为:β=N/M;
(3)假设节点加入网络系统的过程服从Poisson分布,且加入的速率是λ;
(4)假设CP在网络系统内平均逗留时间是D。并且逗留时间 T服从 f(T)分布,那么 D=∫T×f(T)dT,参考文献[10]指出D大约是 60 min;
(5)假设平均每个CP每秒发出 q个请求(资源索引和信誉评估请求)。
基于以上假设,可知:网络模型中平均有N=λ×D个Common Peer[11]。如果知道参数λ和D,则可以由此得出模型中CP节点的数目。反之,如果通过测量知道N,则可以由此得出节点到达速率λ。假设N=1 000 000,D=3 600 s,则得出 λ=278个/s。这表明,该信任模型中每秒可以有278个普通节点的加入和离开,因而该信任模型具有高度动态性和可扩展性。
由假设可知对于SP节点平均要处理查询个数为:R=q×β,每秒要转发的查询数为:Z=(q×N×h)/M,如果每个查询消息的数据包为C字节,那么转发消息所占的带宽为:W=Z×C=q×β×h×C。

4.2 仿真实验
仿真实验利用斯坦福大学开发的P2P模拟器Query Cycle simulator进行仿真,并与模拟器自带的EigenTrust信誉模型进行对比。
(1)交易成功率
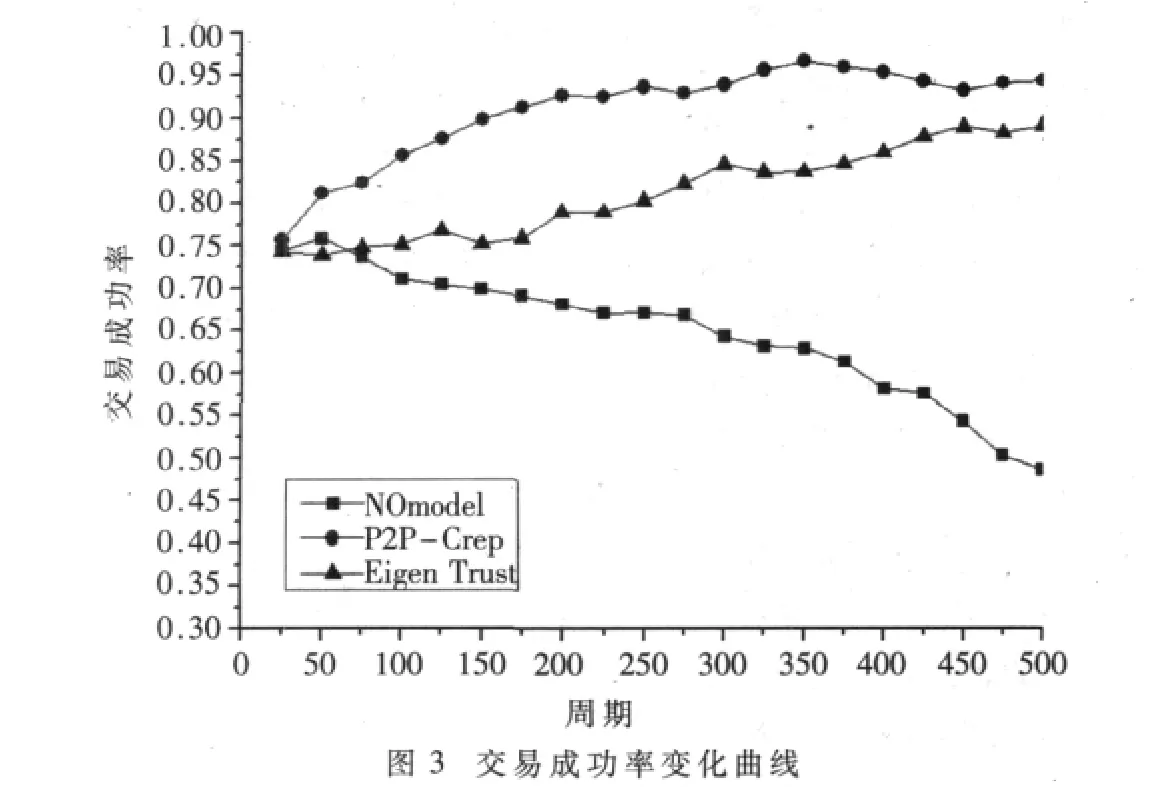
仿真电子商务网在不同查询周期时的交易成功率。实验设定恶意节点的占用率为20%,随着仿真周期增长,P2P-CRep信誉评估算法、没有信誉评估算法以及EigenTrust信誉评估算法对交易成功率的影响变化曲线如图3所示。从图中可以明显地看出,在没有信誉评估模型的电子商务网络中的交易成功率急剧下降,由此,证明对于存在恶意节点的电子商务,很难保证交易的安全性。此外,在不同的仿真周期时,P2P-CRep信誉评估算法比EigenTrust信誉评估算法有较高的交易成功率。
(2)“积小交易信任行大骗”行为
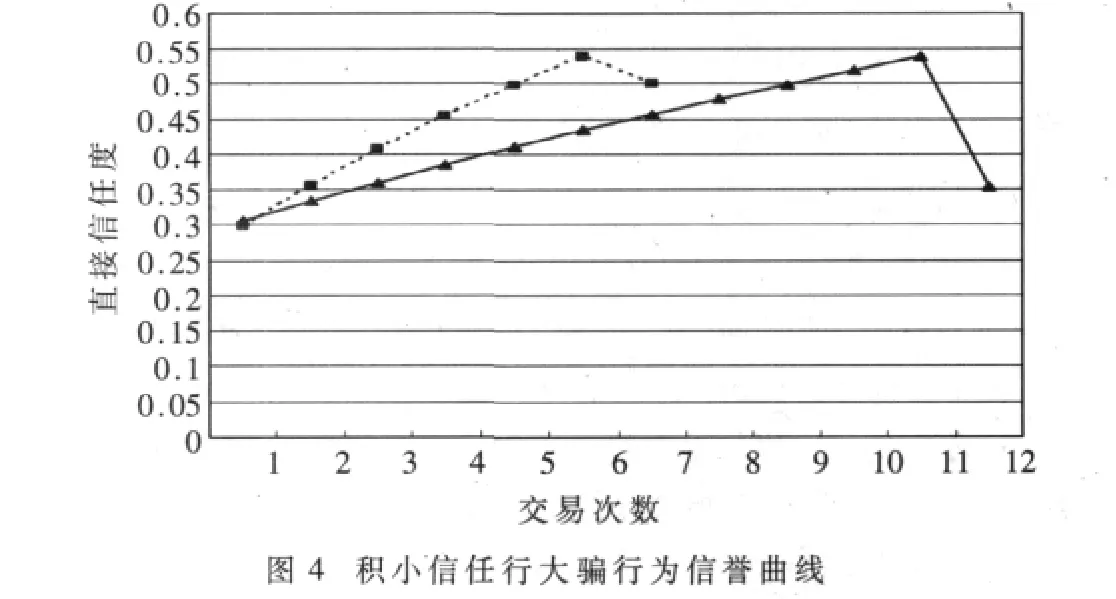
本次实验通过仿真节点对于恶意节点的直接信任度变化曲线来表明信誉模型在“积小交易信任行大骗”行为方面的防御能力。直接信任度的变化曲线如图4所示,虚线和实线分别是对恶意节点PeerA和PeerB的直接信任度变化曲线,其中,虚线中的前6次交易的交易评估因子是0.8,第 7次交易的评估因子是 0.16,实线中的前11次交易评估因子是0.4,第12次交易评估因子为0.8的交易。由图可以看出:PeerA经过11次小交易积累的信任度,1次大的失败交易就损耗完积累的信任度,另外,奖惩的幅度也跟交易规模的大小有关,由此表明P2PCRep具有防御“积小交易信任行大骗”行为的能力。
(3)共谋欺诈的抵御性能
本次实验设定网络中恶意节点为共谋行为的恶意节点,买家恶意节点对商品的评价取值为1的交易评价度。实验仿真恶意节点不断增加时的交易成功率,其仿真结果如图5所示。由图可以明显看出,随着恶意节点数不断曾加,交易成功率都有所下降,但P2P-CRep下降幅度较小,表明P2P-CRep具有较强的抵御能力。
根据基于簇域的P2P拓扑结构的特点,本文提出了P2P-CRep信誉评估模型,以此解决电子商务中的信誉问题。基于簇域的P2P网络大大降低了信誉评估带来的资源开销,解决了信誉数据存储和查询的问题,并且使信誉评估网络系统模型具有高度动态性和可扩展性。在信誉评估算法中实现对电子商务中恶意推荐、积小交易信誉行骗等恶意行为的有效抵御机制,为电子商务中的交易安全提供保障。
[1]Gnutella.[EB/OL].http://www.gnutella.com.
[2]Kazaa.[EB/OL].http://www.kazaa.com.
[3]BETH T,BORCHERDING M,KLEIN B.Valuation of trust in open networks[C].In Gollmann,D.,ed.Proceedings of the 3rd European Symposium on Research in Computer Security-ESORICS’94.Volume 875 of Lecture Notes in Computer Science.,Brighton,UK,Springer-Verlag.1994:3-18.
[4]JØSANG A.A model for trust in security systems[C].In:Proceedings of the 2nd Nordic Workshop on Secure Computer Systems.1997.http://security.dstc.edu.au/staff/ajosang/papers.html.
[5]STOICA I,MORRIS R,KARGER D,et al.Chord:a scalable Peer-to-peer lookup service for internet applications[A].Proceedings of ACM SIGCOMM’01[C],San Diego California,2001:35-89.
[6]韩存,张玉忠.企业绩效评价方法取向研究[J].财会通讯,2005(5):3-7.
[7]夏启志,谢高岗,闵应骅,等.IS-P2P:一种基于索引的结构化 P2P 网络模型[J].计算机学报,2006,29(4):602-610.
[8]李玲娟,姬同亮,王汝传.一种基于信任机制的混合式P2P模型[J].计算机应用,2006,26(12):2900-2902.
[9]张春瑞,徐恪,王开云,等.基于信任向量的 P2P网络信任管理模型[J].清华大学学报(自然科学版),2007,47(7):35-37.
[10]SAROIU S,GUMMADI P.K,GRIBBLE S.D.A measurement study of Peer2to 2Peer file sharing systems[C].In:Proceed-in gs of the Multimedia Computing and Networking Conference,San Jose,alifornia,USA,2002.
[11]宋金龙,董健全,邹亮亮.一种P2P网络安全的信誉度模型设计[J].计算机应用.2006,26(4):833-835.
[12]SCHOLLMIER R.Why P2P(Peer-to-Peer)does scale:analysis of P2P traffic patterns[C].In:Proceeding of the IEEE P2P Computing Conference,Linkoping,Sweden,2002:112-119.


