空间相机主反射镜的拓扑优化设计

刘秀敏，何 斌，沙 巍，张星祥，孙 斌，任建岳

（1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院研究生院，北京 100039）

空间相机主反射镜的拓扑优化设计

刘秀敏1，2，何 斌1，沙 巍1，2，张星祥1，孙 斌1，任建岳1

（1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院研究生院，北京 100039）

为满足空间反射镜高面形精度、高轻量化率的要求，在外径700mm圆反射镜的设计过程中引入拓扑优化方法，依据变密度法建立了SIMP模型。在反射镜光轴方向重力工况下，以结构整体柔度为设计约束，最小体积为设计目标进行迭代，优化设计出了RMS值为8.89nm，轻量化率达82％的反射镜模型。在同等质量下，基于传统的三角形轻量化孔结构设计出的反射镜模型RMS值为11.75nm，轻量化率为65％。在径向重力工况下，拓扑优化结构也能满足面形要求。计算结果表明，拓扑优化的轻量化形式在面形和轻量化率上都优于传统形式。

空间反射镜；拓扑优化；镜面面形

1 引言

随着空间光学遥感器观测精度的不断提高，对其主要光学元件的精度要求也越来越高。主镜作为空间光学遥感器的关键件之一，对它的要求是质量轻，且镜片的可加工性好，不致于在外载荷的作用下产生面形精度超差。由于主镜是光学遥感器中具有大集中质量的光学元件，其质量的增加，会使整机质量增加，成本上升；同时动力学特性也发生改变，导致整机自振频率的下降，抵抗整机运行过程中常见的低频振动能力降低，所以轻量化主镜在重量减小的同时，不仅能改变自身性能，还可以改善光机系统的力学性能［1］。

拓扑优化设计处于结构的概念设计阶段，其主要思想是把寻求结构的最优拓扑问题转化为在给定的设计区域内寻求材料的最佳分布问题［2］。具体来说就是在一个确定的连续区域内寻求结构内部非实体区域位置和数量的最佳配置，以及结构中的构件布局及节点联结方式最优化，使结构能在满足应力、位移等约束条件下，将外载荷传递到结构支撑位置，同时使结构的某种性态指标达到最优。本文将拓扑优化方法引入了一个外径为700mm的圆反射镜的设计过程，利用拓扑优化进行主反射镜的轻量化结构设计，克服了传统主反射镜参数化设计的局限性，完成了设计所要求的轻量化主反射镜的最佳拓扑结构形式。

2 拓扑优化理论基础

2.1 基本理论

变密度法是连续体拓扑优化的常用方法，属于材料描述方式。该方法的基本思想是引入一种假想的密度，即O-1的可变材料，指定每个有限单元的密度相同，并以每个单元的相对密度为设计变量。当单元相对密度z＝0时，表示该单元无材料，单元应删除；当单元相对密度z＝1时，表示该单元有材料，应保留或增加该单元。变密度法直接假定相对密度与材料弹性模量之间的非线性对应关系［3］。其中应用得比较多的模型是SIMP（Solid Isotropic Microstructure with Penalization）法，其材料模型为：

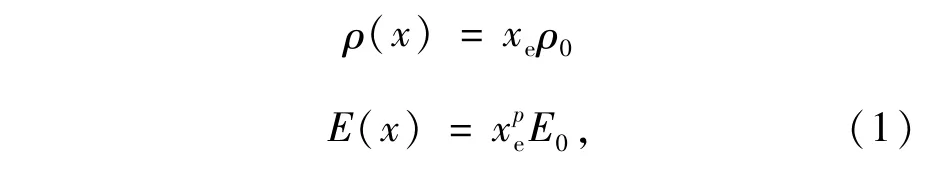
式中：xe为每个单元的相对密度，ρ（x）为拓扑优化设计变量，ρ0为设计区域每个单元的固有密度，E（x）为优化后的弹性模量，E0为初始弹性模量，p为惩罚因子［4］。

2.2 数学求解方法

目前，结构拓扑优化的数学求解方法主要分为优化准则法、数学规划法和遗传算法［5］。

早期的结构（特别是航空结构）设计使用的是直觉的准则法，如满应力设计，同时破坏模式和均匀能量密度方法。优化准则法不需要导数信息，对设计变量的增加不敏感，迭代次数少，计算效率高，还由于概念简单，容易编程，特别适合于工程实际的应用。但另一方面，优化准则法需要建立准则和相应的迭代公式，而建立准则和迭代公式的理论依据尚欠充分，且与研究问题的特点有关，缺乏通用性。所以，优化准则法不能保证收敛到最优解，甚至不能收敛到局部最优解，或不收敛。

在数学规划方法中，结构设计成为被一些应力、位移和频率等行为函数约束的多维设计空间中的目标函数的极值问题，可采用线性和非线性规划得到极值解。数学规划不仅要进行结构分析，还需要计算每个设计变量的导数，特别是实际问题中变量较多时，优化效率很低，运算费用太高。

遗传算法是借鉴生物进化的原理产生的一种人工智能算法。遗传算法更适于寻找全局最优解，且可以同时找到几个局部最优解，不需要目标函数的导数信息，具有理论模型简单等优点。尤其是对离散变量的寻优，更有独到之处，但目前算法的计算效率还有待进一步提高。

2.3 反射镜拓扑优化的数学模型

结构设计中经常以刚度最大化或应变能最小化作为优化的目标函数，以结构整体的体积约束作为优化的约束条件，在给定载荷和位移边界条件下，基于密度函数模型建立线弹性结构拓扑优化设计的静力状态下的数学模型为：

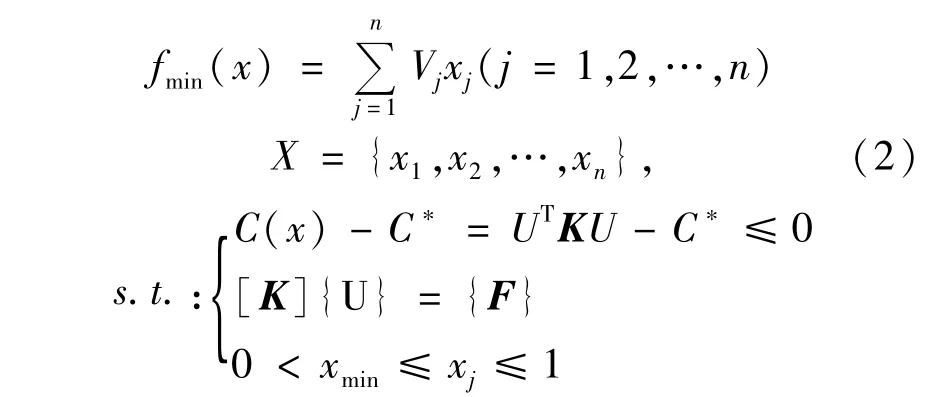
式中，Vj为优化后的单元体积，xj为单元设计变量，C（x）-C*≤0为结构的总体柔度约束，U为位移列阵，K为结构总体刚度矩阵，F为力向量，xmin为单元设计变量下限（引入密度xmin下限的目的是防止单元刚度矩阵奇异），n为结构离散单元总数。

在反射镜模型中，将对结构刚度（柔度）的要求转化为对镜面节点的位移量要求，从而柔度响应可以用镜面节点的总位移来代替。将体积分数定义为响应，根据数学模型，取镜面节点总位移最大10nm作为约束上限，以最小体积为目标进行迭代。

3 反射镜拓扑优化模型求解

3.1 反射镜模型

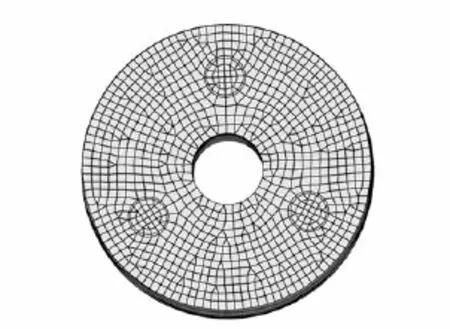
图1 反射镜有限元模型Fig.1 FEM of themirror

研究对象为空间光学遥感器的主反射镜（如图1），外径为700mm，内径为175mm，镜面为凹球面，背部为平背形，材料为碳化硅［6］。定义光轴方向为地面的法向，此工况下，反射镜采用背部三点支撑方式［7］，由背部支撑提供支撑力。本文是在光轴与地面垂直时在自重作用与背部支撑综合工况下对反射镜进行拓扑优化的。

图2为模型设计区域和非设计区域定义情况，因为必须要保证反射镜镜面的完整性及3个支撑孔具有一定的壁厚，所以将支撑孔孔壁（5mm）和反射镜面（5mm）等区域排除在设计区域以外。

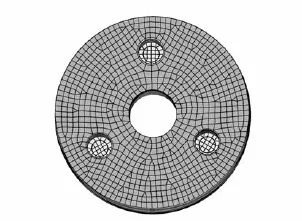
图2 反射镜拓扑优化模型Fig.2 Original topologicalmodel

图3 拓扑优化流程Fig.3 Flow chart of topological optimization

3.2 优化的应用

利用OPTISTRUCT优化软件，对主镜进行连续体拓扑优化，流程如图3所示。经过迭代分析计算，得到了主反射镜最终拓扑结构形式。优化后的轻量化形式如图4所示，拓扑优化得到的轻量化形式并不能直接应用于工程，需要根据要求将此形式稍作改动，将轻量化形式转换为较容易加工的加强筋形式（图5），进而在不改动拓扑形式的情况下达到最佳工艺性。

图4 拓扑优化结果Fig.4 Topological optimization result

图5 拓扑优化模型Fig.5 Mirrormodel after topological optimization

3.3 优化结果及对比

为比较拓扑优化后反射镜的PV和RMS值，建立了比较模型（图6），三角形轻量化孔相对于正方形、六边形和扇形轻量化孔在自重变形和热变形两个方面的表现都相对突出，同时也能达到相当高的轻量化率［8］。在轴向重力工况下对两模型进行对比计算得到轴向变形云纹图，如图7和图8所示。

图6 三角形轻量化孔模型Fig.6 Model of triangular lightweight hole

图7 拓扑优化结构变形云纹图（轴向）Fig.7 Displacement contours of optimized topological model（axial）

图8 对比结构变形云纹图（轴向）Fig.8 Displacement contours of contrastive model（axial）

常规方式和拓扑优化方式的反射镜模型PV和PMS值的对比结果列于表1。

表1 方法对比（轴向）Tab.1 Com parison ofmethods（axial）

从表1可以看出，拓扑优化的轻量化结构与常规优化结构均能满足镜面面形要求，但是经拓扑优化方法得到的反射镜结构不仅在面形和轻量化率上优于常规结构，在一阶频率上也优于常规结构。拓扑优化是在轴向重力工况下寻优得到的，而反射镜在径向重力工况下的面形值也需要考虑，在径向重力工况下对两模型进行对比计算，得到变形云纹图（图9、图10）、PV和RMS值（表2）。

图9 拓扑优化后的变形云纹图（径向）Fig.9 Displacement contours of optimized topological model（radial）

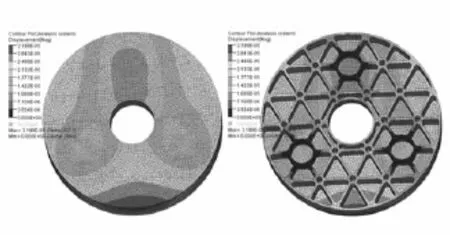
图10 对比模型变形云纹图（径向）Fig.10 Displacement contours of contrastivemodel（radial）

由于拓扑优化是针对轴向重力工况下，保证轴向刚度情况下实现的最小体积设计，所以在其他工程参数上可能会有所降低。拓扑优化的目标一般是工程中比较重要的参数，其他较次要的参数指标如果在设计中有所下降，只要依然在允许范围内，即认为拓扑优化设计是可行的。如果存在多个重要参数，则可以在模型中添加多个设计约束，从而达到满足多个要求的优化结果。

从表2中的数据可见，针对轴向重力方向对反射镜进行拓扑优化，导致径向重力下的面形精度有所下降，不过优化结果完全能满足径向重力工况的设计要求。综合考虑以上两种工况，可以说明拓扑优化方法得到的反射镜轻量化结构优于常规轻量化结构［9］。

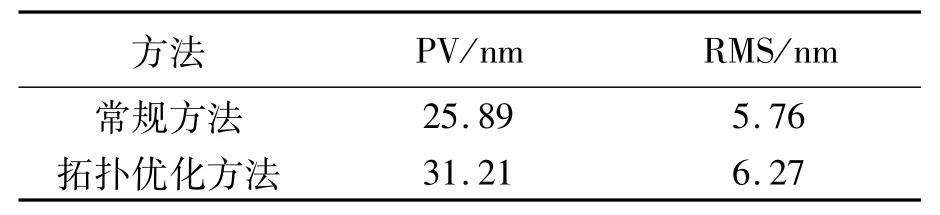
表2 方法对比（径向）Tab.2 Comparison ofmethods（radial）

4 结论

本文将拓扑优化设计方法应用在空间光学遥感器主反射镜的轻量化设计中，得到了满足面形要求及较高轻量化率的最佳主反射镜轻量化结构。该方法打破了主反射镜传统的设计思路，理论性强、目的明确、效率高，是一种新型的设计方法。该方法也可以推广到其它部件的设计上，为机械设计人员提供全新的设计方案，进而得到更合理的结构。

［1］吴清文.空间相机中主镜的轻量化技术及其应用［J］.光学精密工程，1997，5（6）：69-78.

WU QW.Light-weight technology and its application of primarymirror in space camera［J］.Opt.Precision Eng.，1997，5（6）：69-78.（in Chinese）

［2］LU CH M.Topology optimization in structural design［D］.Arlington：The University of Texas，1994.

［3］李延伟，杨洪波，耿麒先，等.大口径主反射镜轻量化结构拓扑优化设计方法［J］.光学技术，2008，34（2）：236-238.

LIYW，YANG H B，GENG Q X，et al.Large-aperture lightweight primarymirror design method using topology optimization［J］.Opt.Technique，2008，34（2）：236-238.（in Chinese）

［4］彭禹，郝志勇.基于动力学仿真的零件拓扑优化方法研究［J］，2007，18（8）：976-978.

PENG Y，HAO ZH Y.Research on dynamics-simulation-based topology optimization solution［J］，2007，18（8）：976-978.（in Chinese）

［5］周克民，李俊峰，李霞.结构拓扑优化研究方法综述［J］.力学进展，2005，35（1）：69-76.

ZHOU K M，LI JF，LIX.A review on topology optimization of structures［J］.Adv.Mechanics，2005，35（1）：69-76.（in Chinese）

［6］高明辉，刘磊，任建岳.空间相机反射镜碳化硅材料性能测试［J］.光学精密工程，2007，15（8）：1170-1174.

GAO M H，LIU L，REN JY.Characteristic test of sic for space camera′smirror［J］.Opt.Precision Eng.，2007，15（8）：1170-1174.（in Chinese）

［7］关英俊，辛宏伟，赵贵军，等.空间相机主支撑结构拓扑优化设计［J］.光学精密工程，2007，15（8）：1157-1163.

GUAN Y J，XIN HW，ZHAOG J，etal..Topologic optimization design formain supporting structure of space camera［J］.Opt.Precision Eng.，2007，15（8）：1157-1163.（in Chinese）

［8］俞天野，贾建军.大口径主反射镜的轻量化方案设计［J］.红外，2007，28（8）：6-10.

YU T Y，JIA JJ.Lightweight design of large-diametermirror［J］.Infrared，2007，28（8）：6-10.（in Chinese）

［9］沙巍，陈长征，张星祥，等.空间反射镜轻量化结构的拓扑优化设计［J］.光电工程，2009，36（4）：35-39.

SHA W，CHEN CH ZH，ZHANG X X，et al..Topological lightweight design of space mirror［J］.Opto-electronic Eng.，2009，36（4）：35-39.（in Chinese）

Topological lightweight design of primary m irror in space camera

LIU Xiu-min1，2，HE Bin2，SHAWei1，2，ZHANG Xing-xiang1，SUN Bin1，REN Jian-yue1
（1.Changchun Institute of Optics，FineMechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.Graduate University of Chinese Academy of Sciences，Beijing 100039，China）

In order to satisfy the strict requirements of the surface-shapes and lightweight ratios for spacemirrors，the topologicalmethod was introduced to design the reflectmirror with aФ700mm.According to the densitymethod，the Solid Isotropic Microstructure with Penalization（SIMP）model was established.In the condition of axial-oriented gravity，by taking the general flexibility as a design constraint，and the minimum volume as a design objective，a better structure with a RMSof8.89nm and a lightweight ratio of82％was obtained after iterations.In the same weight，the conventional triangular lightweight structure shows its RMS in 11.75nm and lightweight ratio in 65％.In the condition of radial-oriented gravity，the surface-shape of the topological structure alsomeets the requirements of the design.In the considerations of the surface-shape and lightweight ratio，the computational result shows that the topological optimizationmethod is better than the conventionalmethod.

spacemirror；topological optimization；surface-shape

国家863高技术研究发展计划资助项目（863-2-5-1-13B）

1674-2915（2010）03-0239-06

V475.3；TH703

A

2010-01-22；

2010-03-16

刘秀敏（1985—），女，河北衡水人，硕士研究生，主要从事空间光学仪器CAD/CAE方面的研究。E-mail：liuxiumin1126@126.com

何 斌（1961—），男，吉林长春人，研究员，主要从事空间光学遥感器技术方面的研究。E-mail：hbemail@163.com