基于SVM方法的太阳总辐射值的估算

彭怀午，杨晓峰，刘方锐

（1.内蒙古电力勘测设计院，内蒙古自治区呼和浩特市 010020;2.华中科技大学电气与电子工程学院，湖北省武汉市 430074）

0 引言

进行太阳能光伏或光热电站设计时，太阳总辐射是一个重要的参数。然而，在很多地区，尤其是太阳能资源非常丰富的西部偏远地区，没有太阳总辐射的观测资料，常常需要根据当地气象站的其他观测参数对太阳总辐射进行估算。Kimball[1]发现太阳总辐射和日照时间存在近似的线性关系；Angstrom[2]最早提出了利用晴天（可能）太阳总辐射和日照百分率计算月太阳总辐射的气候学方法。此后，这种经典的线性关系被广泛用来计算太阳总辐射值[3]。

目前，我国常用太阳总辐射计算公式中的起始值主要分为3种，分别采用晴天太阳总辐射[4]、天文总辐射[5]和理想大气总辐射[6]。和清华等[7]分析了3种不同起始值的预测精度，发现采用天文总辐射的误差较小。同时，有不少文章利用当地气象站资料，对该区域的太阳总辐射值进行了估算[8-11]。

本文主要针对基于支持相量机的太阳总辐射值估算进行研究，并与传统的线性方法进行了对比分析。实测数据验证了采用以支持向量机（SVM）方法进行太阳总辐射值估算的可行性和准确性。

1 资料与方法

利用公开的澳门气象站1998年—1999年的逐日太阳总辐射值、逐日日照时间和逐日日照百分率资料作为样本。逐日日照时间和逐日日照百分率用来进行相互验证，保证输入资料的准确性。澳门位于我国大陆东南部沿海，正当珠江口西岸。其经纬度位置为：北纬22°11′，东经113°32′。1998年的数据用来学习，1999年的数据用来验证估算值的准确性。

对于传统的线性方法估算太阳总辐射，按照《太阳能资源评估方法》[12]，用如下经验公式进行计算：

式中，Q0为天文辐射量，采用文献[12]中的方法计算得到；S为日照时数百分率；a,b为经验系数，根据计算点附近的日射站观测资料，利用最小二乘法计算求出。

Vapnik[13-14]提出的支持向量机（SVM）以训练误差作为优化问题的约束条件，以置信范围值最小化作为优化目标，即SVM是一种基于结构风险最小化准则的学习方法，其推广能力明显优于一些传统的学习方法。

预测输出函数为：

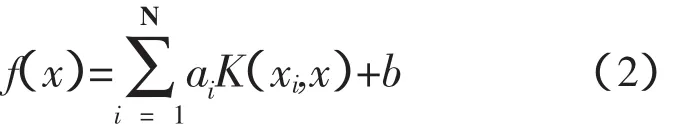
其中，ai是优化过程中对应的拉格朗日系数；b是阀值常数。SVM方法是寻求全局最优，实际上演化为求一个二次规划问题找到最优的ai。目标函数为：

约束条件：

其中，C为惩罚因子，ε为敏感损失函数。

2 估算精度的描述

为了定量地判断最佳估算方法，本文采用两种误差指标来进行方法间的相互评价和比较：一种是均方根误差（RMSE），一种是平均百分比误差（MAPE）。

如果Y（t）是在时间t实际测量的值，F（t）代表同一时间的预测值，则误差定义为：

均方根误差（RMSE）定义为：

平均百分比误差为：

其中n是时间点的个数。

3 估算结果和分析

采用支持向量机（SVM）进行太阳总辐射估算，其计算流程就是首先通过核函数定义的非线性变换将输入空间变换到一个高维空间，输出是中间节点的线形组合，每个中间节点对应一个支持向量。

以1998年数据为样本，线性方法采用公式（1），拟合出一个线性关系，用来估算1999年逐日的太阳总辐射值。

SVM方法[15]采用1998年完整一年的逐日日照百分率和理论计算得到的日天文辐射量作为输入，学习1998年全年逐日的太阳总辐射值。基于学习得到的非线性函数关系，将1999年完整一年的逐日日照百分率和理论计算得到的日天文辐射量作为输入,预测1999年全年逐日的太阳总辐射值。

采用传统线性方法计算得到的预测值与实际测量得到的日太阳总辐射关系，如图1所示。当实测日太阳总辐射值小于10（MJ·m-2）/d时，线性方法的预测值变化较小，接近直线，此时误差较大；而当实测日太阳总辐射值大于15（MJ·m-2）/d时，散点比较集中，估算比较准确。整体的决定系数R2=0.846，相关关系比较显著。

图1 线性方法的预测值和实测值的比较

基于SVM方法预测得到的结果与实际测量得到的日太阳总辐射关系，如图2所示。散点在拟合直线两侧分布比较均匀，同样存在当实测日太阳总辐射值大于15（MJ·m-2）/d时，散点比较集中的现象。整体的决定系数R2=0.8768，相关关系较线性方法更为显著。

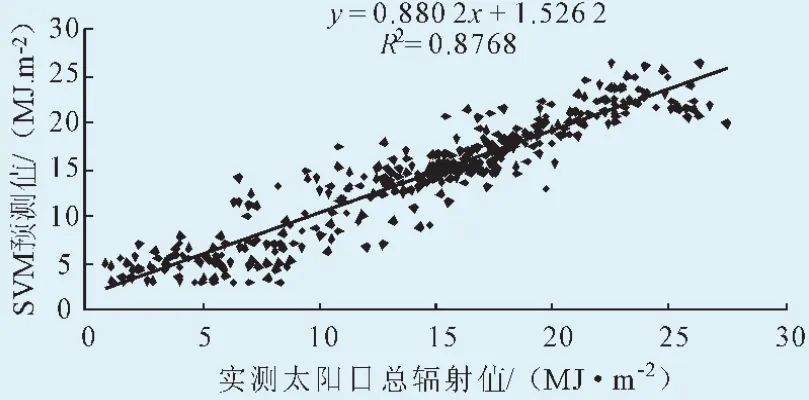
图2 SVM方法的预测值和实测值的比较

2种方法计算得到的日总辐射误差如表1所示，线性方法的平均百分比误差超过30%，均方根误差达到2.54（MJ·m-2）/d，而SVM方法的平均百分比误差下降8%，均方根误差下降0.27（MJ·m-2）/d。

表1 二种方法计算得到的日总辐射误差

将每月逐日的日太阳总辐射相加得到每月的太阳总辐射量，预测值与实测值的对比曲线如图3所示。因为正负误差的抵消关系，2种方法的预测曲线与实测曲线均比较吻合。

图3 两种方法的预测值和实测值的比较

如表2所示，月太阳总辐射估算值的平均百分比误差下降明显，线性方法的平均百分比误差略大于5%，而SVM方法的百分比误差小于5%；线性方法的均方根误差达到26（MJ·m-2）/month，而SVM方法均方根误差为21（MJ·m-2）/month。

表2 二种方法计算得到的月总辐射误差

4 结论

在对澳门地区进行太阳总辐射估算的例子中，比较了传统线性方法和SVM方法的计算结果，得到如下结论。

1）对于日太阳总辐射的估算，在日太阳总辐射值大于15（MJ·m-2）/d时，2种方法的估算值与真实值比较接近。整体的平均百分比误差较大，超过20%。

2）对于月太阳总辐射的估算，由于预测值与真实值的正负误差的抵消效果，整体的平均百分比误差下降明显，约为5%。

3）无论是对日太阳总辐射的估算，还是月太阳总辐射的估算，SVM方法的计算精度均高于传统的线性方法，但其计算模型更为复杂。

[1]Kimball HH.Variations in the Total and Luminous Solar Radiation with Geographical Positions in the United States[J].Mon.weather rev.,1919,47（11）:769-793.

[2]Angstrom A.Solar and Terrestrial Radiation[J].Quarterly Journal of Royal Meteorological Society,1924，50:121-126.

[3]翁笃鸣.中国辐射气候[M].北京:气象出版社,1997.

[4]左大康,王懿贤,陈建绥.中国地区太阳总辐射的空间分布特征[J].气象学报,1963,33（1）:78-95.

[5]翁笃鸣.试论总辐射的气候学计算方法[J].气象学报,1964,34（3）:304-315.

[6]王炳忠,张富国,李立贤.我国的太阳能资源及其计算[J].太阳能学报,1980,1（1）:1-9.

[7]和清华,谢云.我国太阳总辐射气候学计算方法研究[J].自然资源学报,2010,25（2）:308-319.

[8]刘绍民,李银芳.新疆月太阳总辐射气候学计算方法的研究[J].干旱区地理,1997,20（3）:75-81.

[9]杜尧东,毛慧琴,刘爱君,等.广东省太阳总辐射的气候学计算及其分布特征[J].资源科学,2003,25（6）:66-67.

[10]王建源，冯建设，袁爱民.山东省太阳辐射的计算及其分布[J].气象科技，2006，34（1）：98-101.

[11]字春霞.南宁市太阳能日辐射估算方法探讨[J].广西气象，2006，27（1）:31-33.

[12]中国气象局.太阳能资源评估方法（QX/T 89-2008）[M].北京：气象出版社，2008.

[13]Vapnik V N.The Nature of Statistical Learning Theory[M].NY:Springer-Verlag,1995.

[14]Cortes C，Vapnik V.Support-vector Network[J].Machine Learning，1995，20（3）:273-297.

[15]彭怀午,杨晓峰,刘方锐.基于SVM方法的风电场短期风速预测[J].电网与清洁能源,2009,25（7）:48-52.