风电并网的静态电压稳定性研究

廖成滨，温步瀛，江岳文

（福州大学电气工程与自动化学院，福建 闽侯 350108）

0 引言

风能作为可再生能源，凭借趋于成熟的风力发电技术以及不断提高的可靠性，目前已成为世界能源的重要组成部分，并且得到迅猛的发展。根据中国风能协会初步统计，截至2009年底，我国风电机组装机规模为25 805 MW，居世界第二。

随着风电并网容量的不断增加，风电输出功率的波动性和随机性给电网的电能质量[1]和安全运行等方面造成越来越明显的影响，使系统的电压稳定问题更加复杂化。目前，风电场的电力系统的静态电压稳定问题研究主要针对风电并网后系统的电能质量、确定风电场容量及提高安全稳定裕度等方面[2]，其主要研究方法包括：灵敏度法、最大功率法、特征结构分析法和模态分析法等[2-3]。

不同类型风电机组构成风电场的无功特性存在差异，对系统造成的静态电压稳定性也不同。双馈机组可实现有功和无功的解耦控制，所以相对于普通异步电机，由双馈异步电机对风电场电压稳定性的影响要好很多[4]。本文以双馈机组构成的风电场进行分析。在稳态潮流仿真分析中，根据控制目标的不同，可将双馈机组构成的风电场节点视为PQ节点或PV节点[5]。

本文利用基于连续潮流法的节点电压灵敏度和支路损耗灵敏度指标来分析风电场并网后系统的静态电压稳定问题，并提供相关支路的参与程度和系统的稳定裕度信息，从而有助于提出改善系统电压稳定性的控制措施。

1 风电场数学模型

1.1 双馈风电机组静态数学模型

双馈异步电机的T型等值电路如图1所示，其中，rs为定子电阻；xs为定子电抗；rr为转子电阻；xr为转子电抗；xm为励磁电抗；s为转差率。

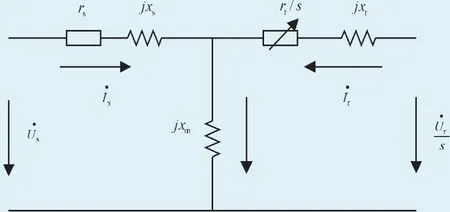
图1 双馈电机等值电路

风电机组的有功功率输出取决于风速的大小。常用变速风电机组的功率曲线大致如图2所示，图2中Vc、Vr、Vf分别为切入风速，额定风速和切出风速。

图2 变速风电机组的功率曲线

由风速功率曲线可确定每台风电机组的有功输出Pe，变频器吸收或发出的无功功率较小，可近似认为变速恒频风电机组的无功功率等于定子绕组的无功功率[6]。当采用恒功率因数方式，功率因数设定为cos φ，风电机组的无功功率可由下式决定：[7]

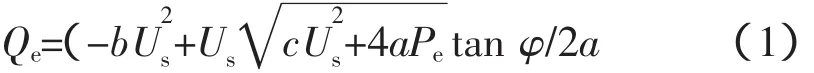
式中，Qe为风电机组的无功功率；Us为机端电压。各参数分别为

1.2 风电场等值模型

考虑风电场内部各台风力机之间的电气联系紧密，对整个风电场进行等值时，可根据风电机组类型和机组变压器参数等因素将风电场等值为单台或多台风电机组，每台等值风电机组作为PQ节点[8]。在本文研究中，对于由n台双馈机组构成的风电场，用一台容量为整个风电场的等值风电机组模型作为近似替代模型，忽略风电场内部线路损耗和变压器损耗，同时假定所有机组的机端电压相同，且等于待求的风电场母线电压。风电场的有功和无功分别表示为：

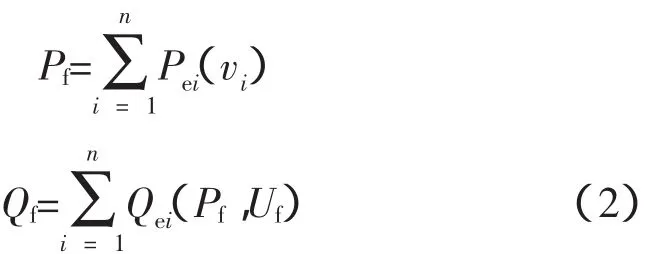
式中，Pf，Qf为风电场总的有功和无功功率；Pei，Qei为第i台风电机组的有功和无功功率；Uf为风电场母线电压；vi为第i台风电机组处的风速。

2 风电场的静态电压稳定分析

在静态电压稳定分析理论中，许多学者采用最大功率观点：将输送功率的极限作为静态电压稳定的临界点，该临界点对应于P-V曲线的拐点。P-V曲线通常通过重复潮流法或连续潮流获得。本文采用常规潮流解法与连续潮流分析方法相结合，可缩短计算时间，同时也能保证解的收敛性。即从初始运行方式开始，用常规潮流法求解至无法收敛后，再采用连续潮流法计算[9]。

应用P-V曲线方法分析风电场的静态电压稳定性时，考虑风电注入系统的功率对电压稳定性的影响，则P代表的是风电场的有功出力，V取风电场接入点电压，V也可以是其他节点或机端等关键节点电压。通过连续潮流获得风电场关键节点的P-V曲线，进而分析风电场关键节点的静态电压稳定问题。

连续（延拓）潮流是电压稳定性分析的有力工具，可以克服潮流方程在接近稳定极限运行状态时的收敛问题。连续潮流法从初始稳定工作点开始，随着负荷缓慢变化，沿相应P-V曲线对下一工作点进行预估、校正，直到勾画出完整的P-U曲线连续潮流计算方法。本文采用局部参数连续法计算系统的静态临界点。其基本方程可描述为：

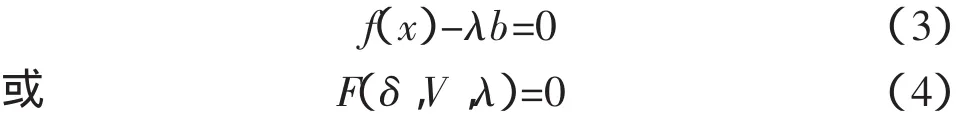
式中，f（x）为常规的潮流方程式，b为系统各节点的负荷增长方式，λ为负荷增长参数（0≤λ≤λcr，λcr为系统在临界点时的负荷增长系数），x为系统的状态变量（x奂(δ，V，λ)，分别为待求的节点电压相角、幅值和负荷增长参数）。

极坐标系统下的常规潮流方程为：

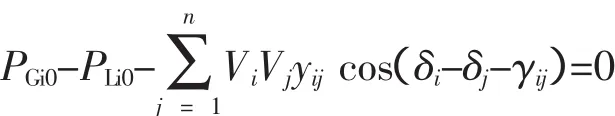
式中，PGi0、QGi0为节点i的发电机出力；PLi0、QLi0为节点i的负荷；Vi、δi为节点i的电压幅值和相角；yij＜γij为节点导纳矩阵第（i，j）个元素。

考虑发电机和负荷的增长，有：

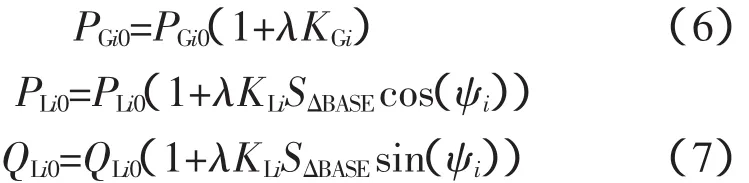
其中，KGi为发电机有功出力变化率的乘子；KLi为负荷变化率的乘子；ψi为节点i负荷变化的功率因数角；SΔBASE为基准视在功率。将式（6）和式（7）代入常规潮流方程有：对于PQ节点：

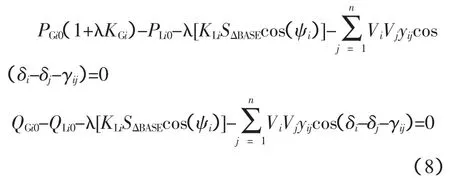
对于PV节点：

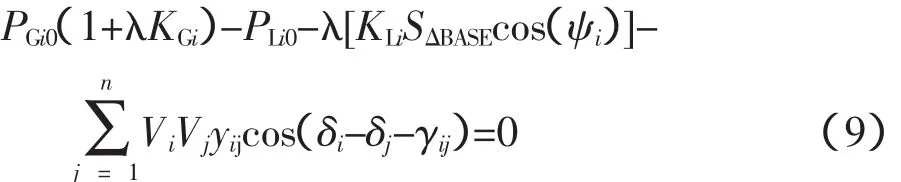
连续潮流法经预估一校正方案寻找随负荷参数变化的潮流解路径，其原理直观如图3所示。

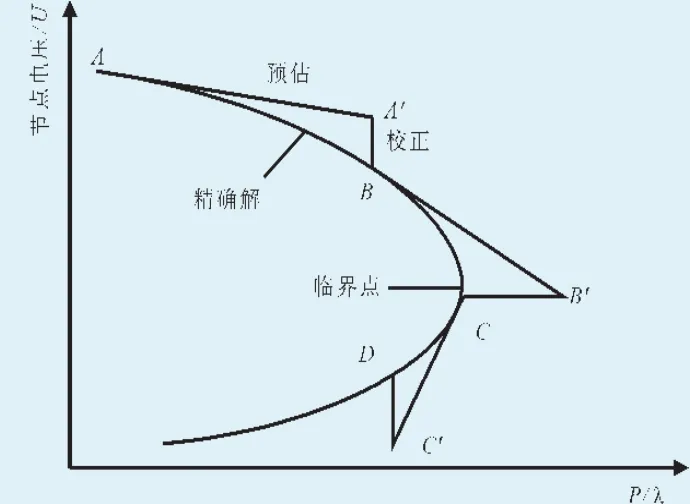
图3 连续潮流法的预估-校正图

1）预估：沿修正后潮流方程的切向量方向寻找其预解时，采取对预解进行线性化估计，即对式（4）求偏导数得线性化的增量方程：

[dδ d V dλ]T即为预估要求的切向量t。因潮流方程引入了参数λ，待求量个数增加了一个，这可通过指定切向量的第k个分量为+1或-1来满足解潮流方程的条件。所设定的分量称为连续（延拓）参数。则由下式对切向量进行求解。

行向量ek的第k个元素为1，与连续参数相对应，其余元素为零。

由上式解得切向量后，就可进行下一步解的预估：

药品化妆品注册管理司主要负责优化药品、化妆品注册和行政许可管理流程，以及承担疫苗监管质量管理体系评估、药品行政保护相关工作。

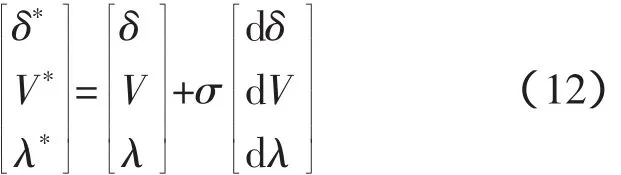
该式中，上标为“*”的分量表示预测值，σ为步长，步长的取值过小会使计算效率较低，而过大的步长又可能导致潮流解不存在，合理选择σ值使其下一步的预测值收敛。

2）校正：以预测值代入扩展潮流方程进行迭代求解。

式中，xk为待求量的第k个分量，其值已被确定；η为预测值的第k个分量。将预测值代入引入附加方程的扩展潮流方程，用牛顿—拉夫逊法迭代求解即可得到校正值。

3 基于连续潮流法的静态电压稳定性指标

3.1 灵敏度指标

通过上节分析，由式（10）不难发现系统静态稳定极限点处的切向量实际上就是系统雅可比矩阵零特征值相应的右特征向量。因此，认为在电压稳定临界点，切向量等于系统雅可比矩阵最小特征值对应的右特征向量，从而利用切向量推导得到相应的电压稳定性指标。

首先找到系统电压稳定的最薄弱节点，该薄弱节点可由d Vi/d Ptotal的最大值决定[10]。d Ptotal为整个系统的负荷变化，本文为风电场有功出力的变化。由下式求d Ptotal：

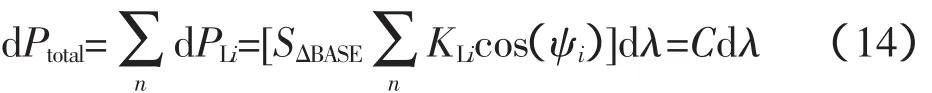
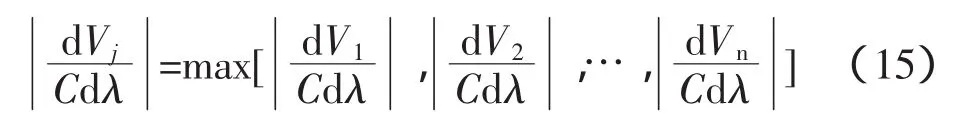
定义随着负荷变量λ变化的标量函数h（x，λ），h（x，λ）可以取系统运行的约束变量，如支路功率，节点电压幅值等。由偏导数的链式法则有：

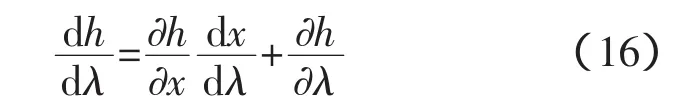
若要计算d h/dλ的值，先要计算d h/dλ（此处x为节点电压的相角和幅值），d x/dλ可直接由连续潮流法求解过程的切向量求得。由此推导出节点电压、支路功率损耗等系统约束量的灵敏度[11]。

3.1.1 节点电压灵敏度

若函数h为节点电压幅值，节点i电压幅值的灵敏度为：

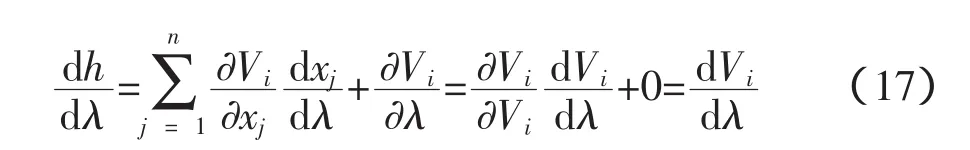
若函数h为节点电压相角，类似可得：

节点电压的灵敏度可用于指示系统接近电压稳定临界点时薄弱节点电压稳定的程度，并且可用于决定系统接近电压失稳的区域。

3.1.2 支路损耗灵敏度

函数h为支路ij的功率损耗Sloss，相应的灵敏度为：

上式的实部和虚部则分别为支路ij的有功损耗灵敏度和无功损耗灵敏度。

3.2 节点电压稳定裕度

在表示系统静态电压稳定储备系数时，常采用有功功率裕度指标[12]，该指标可反映节点承受负荷功率变化的能力。有功裕度即为图3中从初始A点到临界点的水平距离，有功裕度系数表示为：

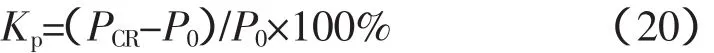
式中，P0和PCR分别为初始运行状态和临界点的有功功率。

4 算例

采用IEEE14节点标准测试系统作为算例系统，风电场通过变压器和110 kV线路接入测试系统（如图4）。系统数据参看文献[13]。

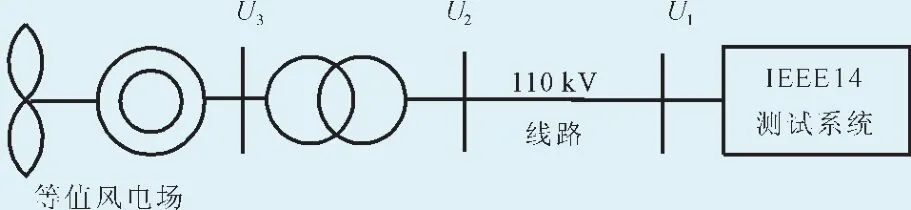
图4 风电场接入IEEE14节点系统图

IEEE14节点系统结构如图5所示。系统接入点分别选择节点14和节点10，除风电场节点外的其他节点的负荷模型采用恒功率负荷模型。风电场经一回40 km架空线LGJ240从110 kV侧接入系统，风电场安装有额定容量1.5 MW的双馈异步力发电机组32台，电机参数为:rs=0.001 692 Ω，xs=0.036 92 Ω，rr=0.002 423 Ω，xr=0.037 59 Ω，xm=1.456 8 Ω，同步转速为1 000 r/min。变压器参数。风力发电机其详细参数见参考文献[14]。基准容量为100 MV·A。

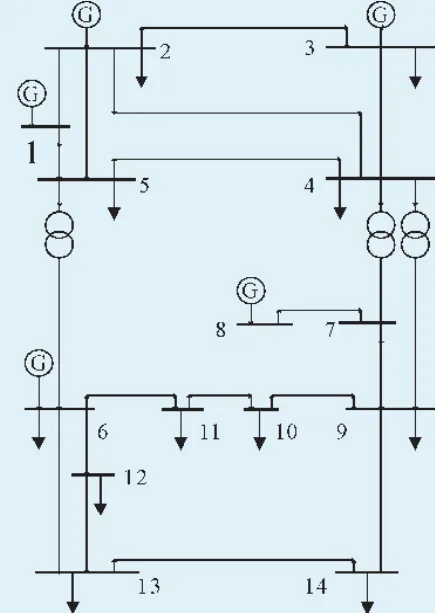
图5 IEEE14节点系统结构

对图4所示的系统进行连续潮流仿真，仿真工具采用MATLAB7.1。以下结果分析都是考虑风电机组功率因数设定为1的情形。风电接入节点14的P-V曲线仿真结果如图6所示，电压U1、U2、U3顺序与图4中编号相同。

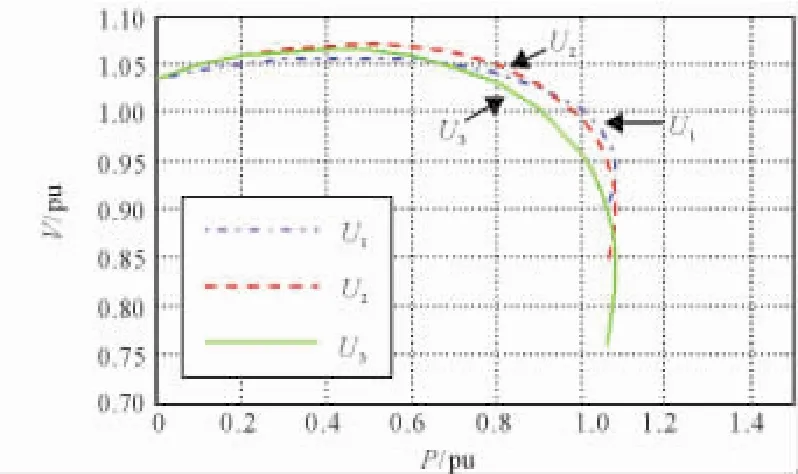
图6 功率因数为1时风电接入节点14的P-V曲线

由图6所示的P-V曲线可知，风电场接入点的电压随注入功率的增加而有所提高，但在高功率注入的运行工况下，母线电压逐渐下降，特别是等值风电场低压侧节点电压U3下降显著。当注入的有功功率P=1.084 2时，系统到达临界点。此时，接入点临界电压为0.819 5，仍然较高，根据文献[12]的分析，实际上节点临界点电压与节点的最大功率极限并无直接关系，因此无法从电压幅值来获得电压失稳的信息。

风电场的系统接入点为节点14时，由式（14）得到系统最弱节点为接入节点14；而接入点为节点10时，最弱节点为节点10，系统的最弱节点与风电不同的系统接入点有关。下表1给出了电压稳定临界点处的节点电压幅值灵敏度，其值均以各情形下的最大值为基准进行归一化，按从大到小排列，其值越大的节点构成了系统的弱稳定区域。风电接入节点14时，构成系统的弱稳定区域的节点为：7、9、10、13和14；风电接入节点10时，构成系统的弱稳定区域的节点为：7、9、10、11和14。不同情形下的弱稳定区域都是风电场接入点的毗邻区域。

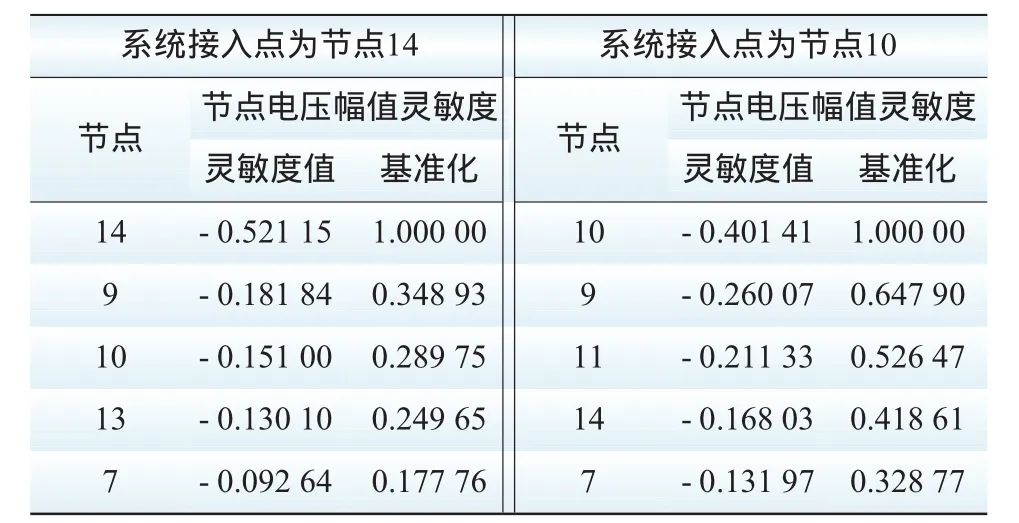
表1 电压稳定临界点处节点电压幅值灵敏度较大的前5个节点

支路灵敏度可说明支路相对于电压稳定性的重要程度。表2显示了电压稳定临界点处，支路的无功损耗灵敏度，由表2可知系统中支路6-13具有较强的无功-电压参与程度。结合支路无功损耗灵敏度与支路的无功损耗分析可知，支路9-14也具有较强的无功-电压参与程序，这一点可从表3中断开不同支路后由连续潮流仿真得到的不同有功裕度验证。由表3可知，若断开支路9-14，相对于支路无功损耗灵敏度大于该条支路的其他支路7-8、6-11和6-12，获得的有功裕度却明显来得要小。

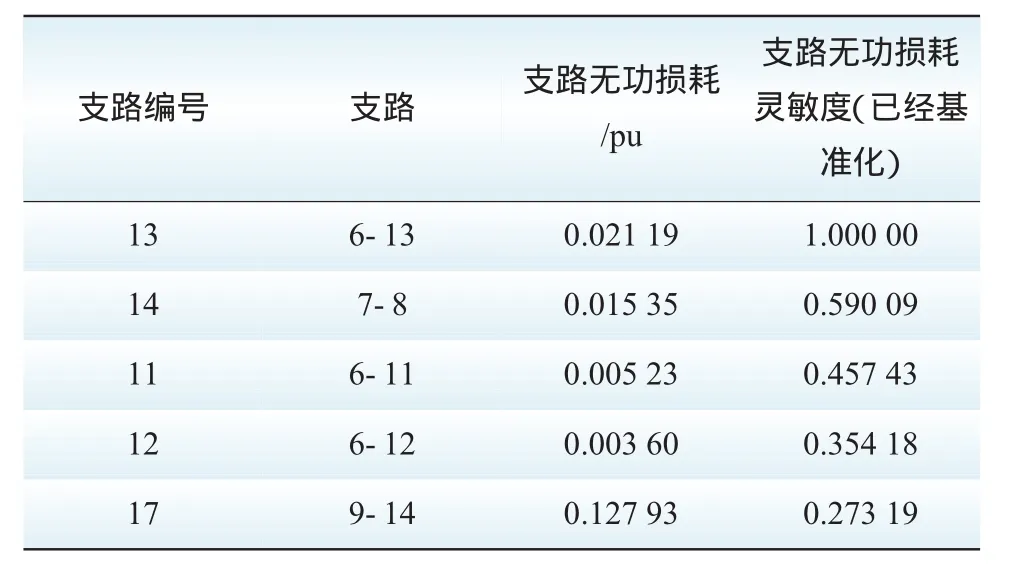
表2 接入节点14时电压稳定临界点处支路无功损耗灵敏度较大的前5条支路

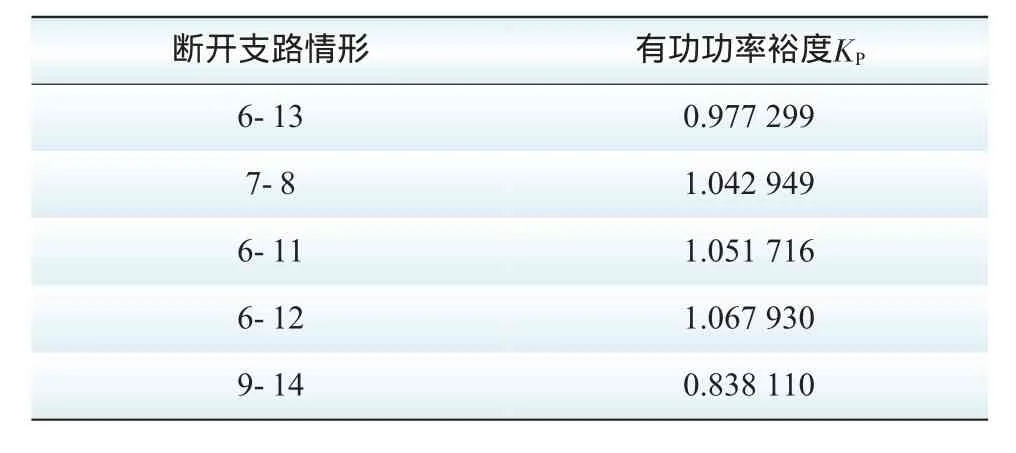
表3 不同支路断开时的有功功率裕度

5 结论

1）利用连续潮流法，克服常规潮流方程在临界点处的奇异问题，绘出风电接入点的P-V曲线，进而确定风电输出的最大临界功率。

2）基于连续潮流法的切向量的相关分析，应用节点电压灵敏度分析相关节点的参与程度，从而确定系统接近临界电压稳定时的弱稳定区域；利用支路无功损耗灵敏度得到相关支路的无功-电压参与程度，并结合支路的无功损耗分析确定了较为重要的参与支路。

[1]孙涛，王伟胜，戴慧珠，等.风力发电引起的电压波动和闪变[J].电网技术，2003，27（12）:62-67.

[2]马幼捷，张继东，周雪松，等.特征结构分析法对风电系统静态电压稳定的研究[J].中国电力，2008，41（03）：87-93.

[3]刘艳妮.风电场并网运行电压稳定性研究[D].北京：北京交通大学，2008.

[4]曹娜，赵海翔，戴慧珠.常用风电机组并网运行时的无功与电压分析[J].电网技术，2006，30（22）：91-94.

[5]胡卫红，王玮，王英林，等.电力系统潮流计算中风电场节点的处理方法[J].华北电力技术，2006（10）：12-15.

[6]郎永强，张学广，徐殿国，等.双馈电机风电场无功功率分析及控制策略[J].中国电机工程学报，2007，27（9）:77-82.

[7]刘艳妮，王玮，王英男.电力系统潮流计算中风电场模型研究[J].华东电力，2008，36（04）:58-61.

[8]曹娜，赵海翔，陈默子，等.潮流计算中风电场的等值[J].电网技术，2006，30（09）:53-56.

[9]潘文霞.大型风电场电压稳定性分析与控制研究[D].南京：河海大学，2004.

[10]Ajjarapu V，Christy C.The Continuation Power Flow:A Tool for Steady State Voltage Stability Analysis[J].IEEE Trans，PWRS，1992，7（1）:416-423.

[11]Battula S.Sensitivity Based Continuation Oower Flow[D].Department of Electrical and Computer Engineering，Iowa State University，1993.

[12]张尧，宋文南.节点电压稳定临界状态和弱节点的确定[J].中国电机工程学报，1993，13（06）:40-45.

[13]张伯明.高等电力系统分析[M].北京:清华大学出版社,1996.

[14]申洪.变速恒频风电机组并网运行模型研究及其应用[D].中国电力科学研究院,2003.