极端恶劣气候条件下的配电系统可靠性分析

李 佳，王海燕，梁 艳，李 勇

（1.山西忻州供电分公司，山西忻州 034100；2.华北电网承德供电公司，河北承德 067000；3.山西西龙池抽水蓄能电站有限责任公司，山西忻州 035503；4.山西忻州供电分公司方元电力勘测设计有限公司，山西忻州 034100）

0 引言

传统的不考虑恶劣气候条件的可靠性预测结果是相当乐观的，其存在着很大误差[1]。像暴风雪、冰冻、飓风这样的灾害气候对电力系统的运行会产生巨大的负面影响。

2008年初，我国南方地区遭受了一场特大冰雪灾害气候的考验，持续了近一个多月[2-3]。尤其是贵州电网，由于遭遇自1951年有气象资料记载以来的罕见大面积严重冰冻灾害天气，使其电网大范围遭受损失，220 kV以下低压配电线路较大范围遭受不同程度损坏，全省很多县市受到停电影响，特别是高寒山区输电线路及电网输送变电设施大面积覆冰，电网的安全运行受到严重威胁。1998年1月，在加拿大魁北克省，东部安大略省发生的“冰风暴”（ice storm）[4-6]灾害气候，导致供电中断用户达到300多万人，致使多于25人死亡。研究表明，如果极端恶劣气候发生的频率和持续时间相对于一般恶劣气候来说很小时，它对长期系统可靠性指标的影响是可以忽略的。据美国和加拿大研究人员预测，极端恶劣气候不仅会变得越来越频繁，而且会越来越严重。重大灾害气候给国民经济和社会各行业造成了巨大的损失，这表明极端恶劣气候条件的影响是不可忽略的，其显著影响着电力系统可靠性水平。

电力系统中，元件故障率应该是气候的连续函数。经验表明，恶劣气候条件下元件发生故障的机率会大大增加，并对元件产生巨大的破坏作用，使输配电网发生多种相关和不相关故障的可能性急剧增加，即出现所谓的“故障聚集”现象[7]。因此，很有必要在可靠性评估中考虑气候条件因素的影响。

IEEE Standard 346将电力系统运行的气候环境按其影响程度分为正常气候（normal weather）、恶劣气候（adverse weather）和极端恶劣气候（灾害）（major storm disaster）3类。文献[8]建立了考虑2种天气状态时可靠性评估的数学模型，对恶劣天气占不同比例时的可靠性指标误差进行了分析，对电网规划和实际操作有一定的指导意义。文献[9]利用3种气候类型，针对不同气候条件下的输电线路元件，建立其可靠性模型，采用Monte-Carlo方法对气候区域和输电线路进行抽样，确定区域气候状态和输电元件状态，比较了计及气候条件与否对可靠性充裕度指标的影响。

本文在传统可靠性分析的基础上，考虑了极端恶劣气候因素，采用三状态气候模型评估某配电系统可靠性水平，并针对极端恶劣气候发生概率的不同来对可靠性指标进行误差分析，保证可靠性分析的客观实际性，说明考虑气候因素对配电系统可靠性的影响有着重大的现实意义。

1 可靠性评估的模型与方法

1.1 三状态气候模型

电力系统是处在不同的气候条件下运行的，元件故障率是气候的连续函数，但是由于系统模拟、数据收集和数据处理等方面存在的困难，很难用连续函数或者许多个离散状态对它加以描述。以往的两状态气候模型[10-11]使用正常与恶劣气候2种状态描述气候环境。近几年随着极端恶劣气候的日益加重，使得我们在对电力系统进行可靠性评估时，不得不遵循实际环境，将极端恶劣气候即灾害气候考虑进来，使用三状态气候模型综合分析系统风险。

图1中给出了气候环境的随机变化状况，这里假设气候持续时间的分布服从指数分布。λn为正常气候时元件故障率的期望值，ni为正常气候的持续时间；λa为恶劣气候时元件故障率的期望值，ai为恶劣气候的持续时间；λm为极端恶劣（灾害）气候时元件故障率的期望值；mi为极端恶劣气候的持续时间。这样可以将气候的随机变化处理为3种气候状态的平均持续时间期望值的模拟过程，如图2所示，N、A、M分别表示正常、恶劣、灾害气候的期望状态持续时间，均服从指数分布。

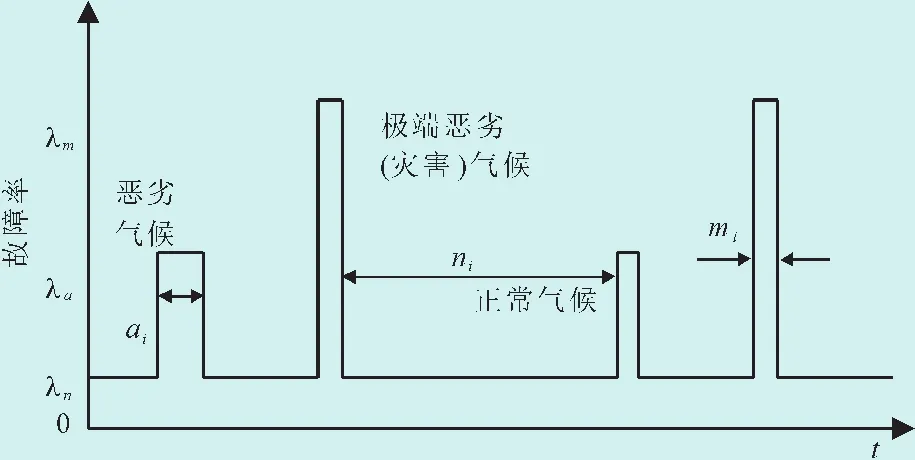
图1 天气随机变化状态图

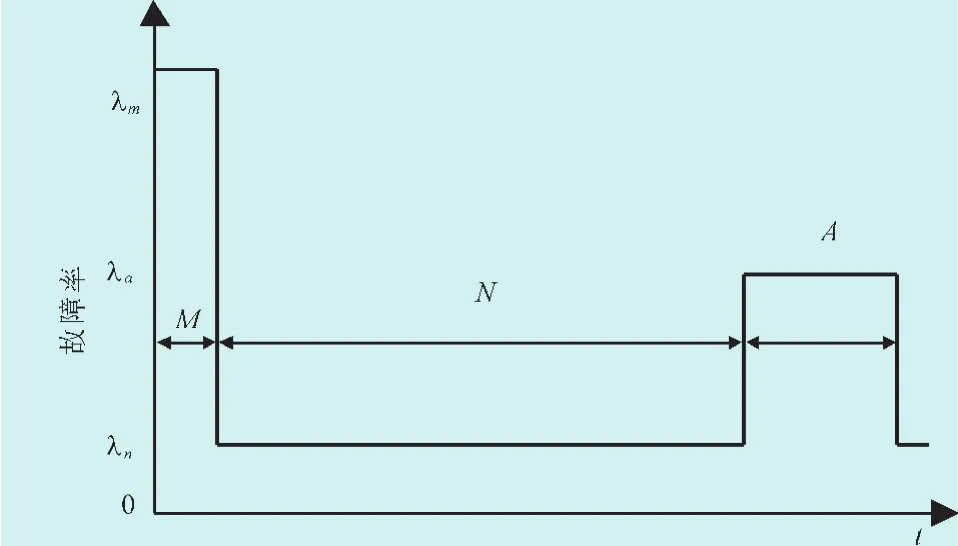
图2 三态气候持续时间期望值

将气候环境按这3种状态分类，建立的气候三状态模型如图3所示，它表征了气候条件在整个可靠性研究周期内，各个状态之间的转移过程。

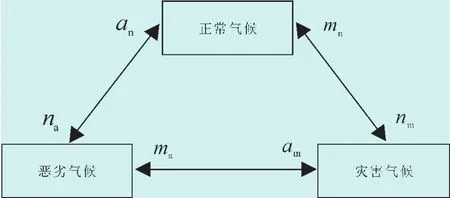
图3 三状态气候模型

图中na为正常气候向恶劣气候的状态转移率，an为恶劣气候向正常气候的转移率，am为由恶劣气候向灾害气候的转移率，ma为灾害气候向恶劣气候的转移率，mn为灾害气候向正常气候的转移率，nm为正常气候向灾害气候的转移率。

本文结合图2和图3，可求出各气候状态的平稳状态概率Pn、Pa、Pm，据此来分析气候因素对可靠性分析的影响。

从图2、图3中，可得到不同气候状态的转移率（次/h）分别为：na=1/N，an=1/A，ma=mn=1/2M，am=nm=1/8 760（1 a为8 760 h）。对图3使用频率平衡法[10]，列出每一种状态的频率方程组如下：

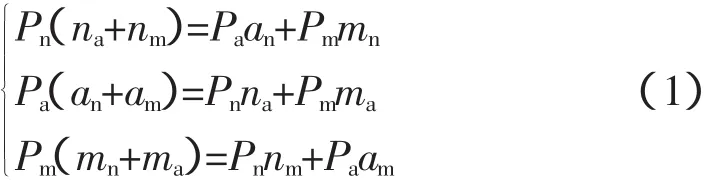
显然上面的方程组中只有2个式子独立，而且由于各气候平稳状态概率之和为1，即：

式中，Pn、Pa、Pm分别为正常气候、恶劣气候、灾害气候的平稳状态概率，可通过方程组（1）中任2个方程与式（2）的联立，求解得到各平稳状态概率，以此考虑气候因素的影响，计算元件可靠性参数。

考虑三状态气候模型后的元件的平均故障率λaverage可由下式表示：

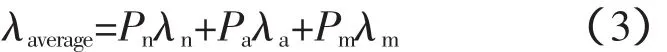
式中λn、λa、λm可由式（4）得到。

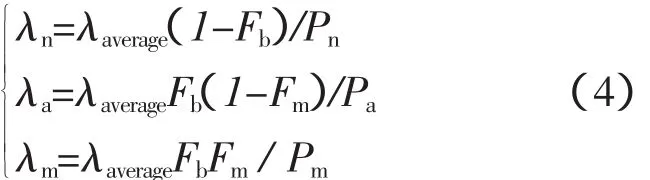
其中，将恶劣气候与灾害气候统称为坏气候（bad weather）[1]，Fb为元件故障发生在坏气候中的百分比，Fm为在灾害气候中发生的元件故障占在坏气候中发生的百分比。

1.2 状态空间分析法

状态空间法的理论基础是马尔柯夫过程，故分析配电系统可靠性的假设条件是由一种状态转移到另一种状态的概率与系统早先的历史无关，即无记'性[12]。一般假定无故障工作时间TTF，故障修复时间TTR均服从指数分布，此时元件转移率则为常数。

当系统中包含m个元件，气候类型为n种，假定每个元件为两状态时，则系统的马尔柯夫模型中共包括2m×n个状态，通过对这些状态的分析来求解系统可靠性指标。下面以双回线路系统（也可认为是二阶故障的情况）的三状态气候模型为例，即系统有2个并联元件，3种气候状态，每个元件只有2种状态即运行和停运状态，则马尔柯夫模型共有12种状态，应用马尔柯夫过程来分析此系统的可靠性指标。对此系统建立状态空间图，如图4所示，元件运行状态用U表示，停运状态用D表示，图中符号μ1、μ2，分别为2个元件的修复率，其余符号含义与前面所述的相同。

图4中，从左至右分别为3种气候状态，从上至下分别为2个元件的4种不同状态组合，从图4可得出转移概率矩阵P，将矩阵P经初等变换可写为P=，其中Q为P除去吸收（故障）状态后的矩阵，由Q可得到基本矩阵N，N=（1-Q）-1，其中I为与Q同维的单位矩阵。

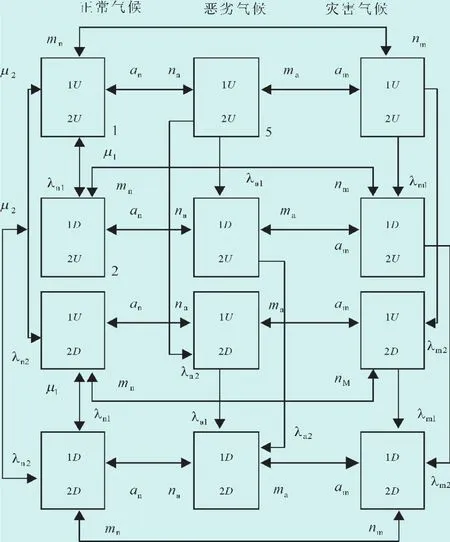
图4 三态气候的两元件系统状态空间图

在基本矩阵N中，从状态1开始至进入吸收状态之前的平均无故障工作时间MTTF1,9可表示为，此时双回线系统的故障率则为：；同样使用频率平衡法[10]可以求出状态空间图中12个系统状态的平稳状态概率P1～P12，从而可求出系统的平均停电持续时间

2 算例分析

在配电系统的充裕度评估中，使用平均停电频率SAIFI（次/用户年），平均停电持续时间SAIDI（h/用户年），平均供电可用率ASAI（%）等可靠性指标来分析，本文使用前面所述理论方法，针对图5所示的某配电系统，从气候的分类不同来进行可靠性评估，计算了3种方案下的可靠性指标，分别为CASE1，传统单状态气候；CASE2，二状态气候，故障发生在恶劣气候百分比F取为50%；CASE3，三状态气候，Fb=50%，Fm=10% 。

这里假设电源是完全可靠的，线路断路器可靠动作率为100%；取线路L1和L2的平均故障率为1.5次/年，L3和L4的平均故障率分别为1次/年、2次/年，修复时间均为10 h/次；负荷1、2的用户数分别为3405、2686户[13]。

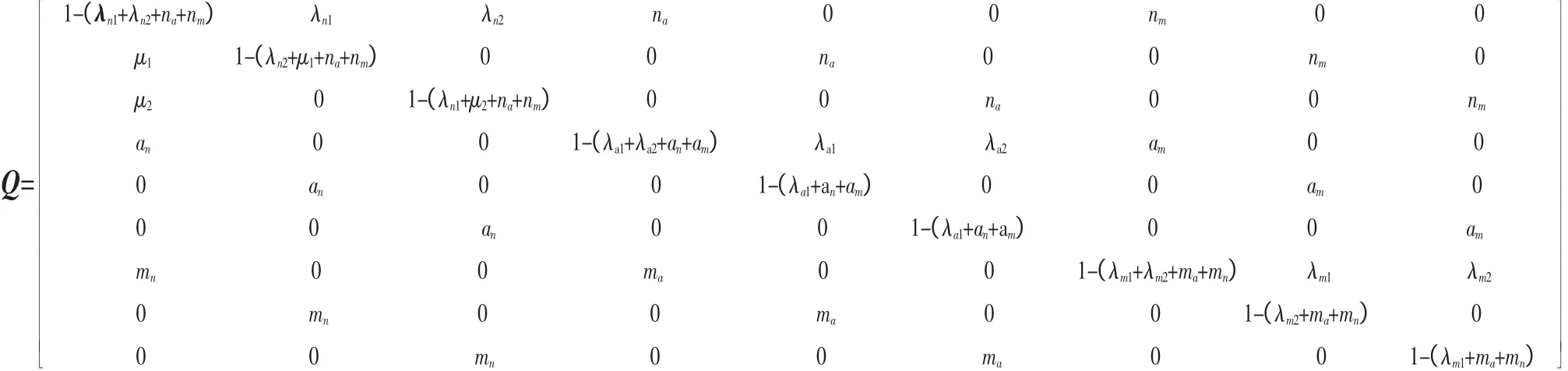
图5 某配电系统单相接线图

由于收集故障发生在各类气候中的数据非常困难，为了说明三状态气候模型的实际影响程度，本文的3种气候状态的期望持续时间值取自文献[1]的经验值，分别假设为N=200 h，A=2 h，M=1 h，且极端恶劣（灾害）气候1 a只发生1次，显然，不同气候状态的转移率分别为：na=1/200，an=1/2，ma=mn=1/2，am=nm=1/8 760，式（1）和式（2）联立，得到正常气候、恶劣气候、灾害气候的平稳状态概率，Pn=0.989 875 25，Pa=0.010 010 61，Pm=0.000 114 14，这样就可以考虑气候因素的影响，得到此配电系统的可靠性评估指标。

表1列出了CASE1-3的各负荷点及系统的可靠性指标，负荷点指标为：故障率λ（次/a），平均停电时间γ（h/次），年停电时间U（h/a）；系统指标为SAIFI、SAIDI和ASAI。从表1可以看出，从CASE1至CASE3，其负荷点及系统的各项可靠性指标均依次增大，图6中示出了2个负荷点的故障率在3种情况下的折线图，可见没有考虑极端恶劣气候情况时，单状态气候、两状态气候条件下的可靠性指标存在一定的误差。在目前灾害性气候日益频繁的环境下，有必要考虑极端恶劣气候因素的影响。

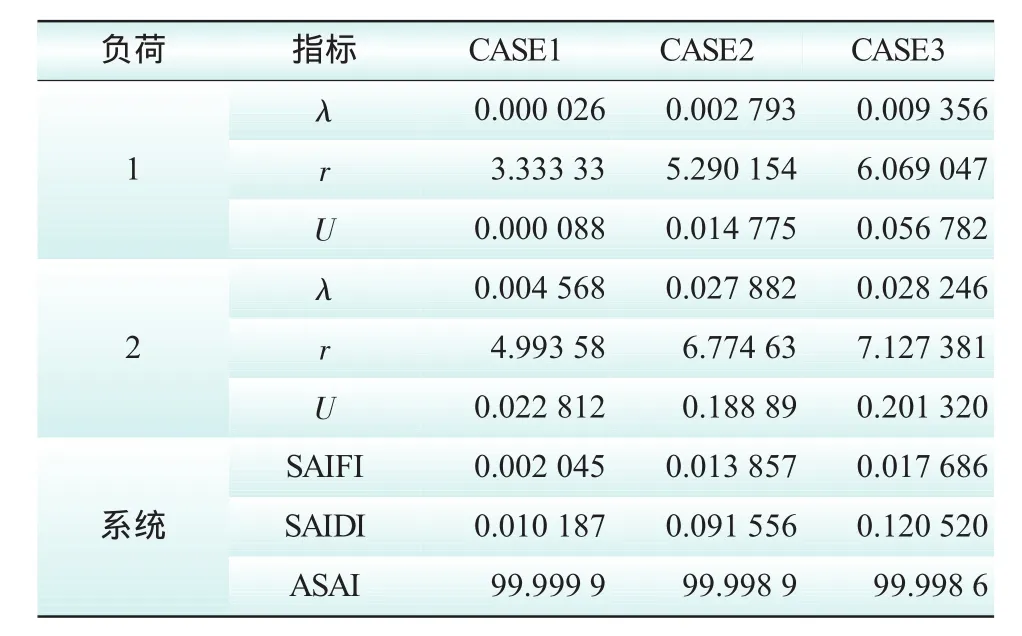
表1 负荷点及系统可靠性指标

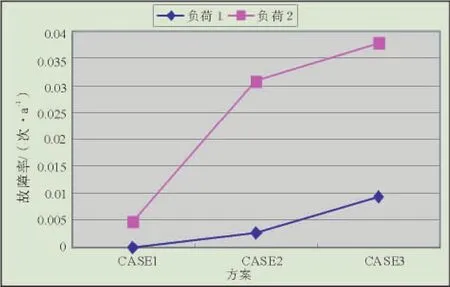
图6 负荷点故障率指标折线图

在上面的CASE3中Fm取为10%，当Fm的值不同时，会使可靠性指标也发生变化，随着Fm的加大，各可靠性指标也随之增大。本文使用针对SAIFI指标而言的误差系数的概念[4，14-15]，用θ来表示，θ=，为传统的单状态气候条件下的系统平均停电频率指标，此处为CASE1中的SAIFI，SAIFIsys为三状态气候条件下的系统指标。在三状态气候模型中，当Fb=50%，Fm发生变化时，其SAIFI误差系数分析见图7所示，当Fm逐渐加大时，误差系数也随之增大。可见，在进行可靠性预测时，如果在评估中未考虑变化的气候环境，其预测结果有着显著的误差。

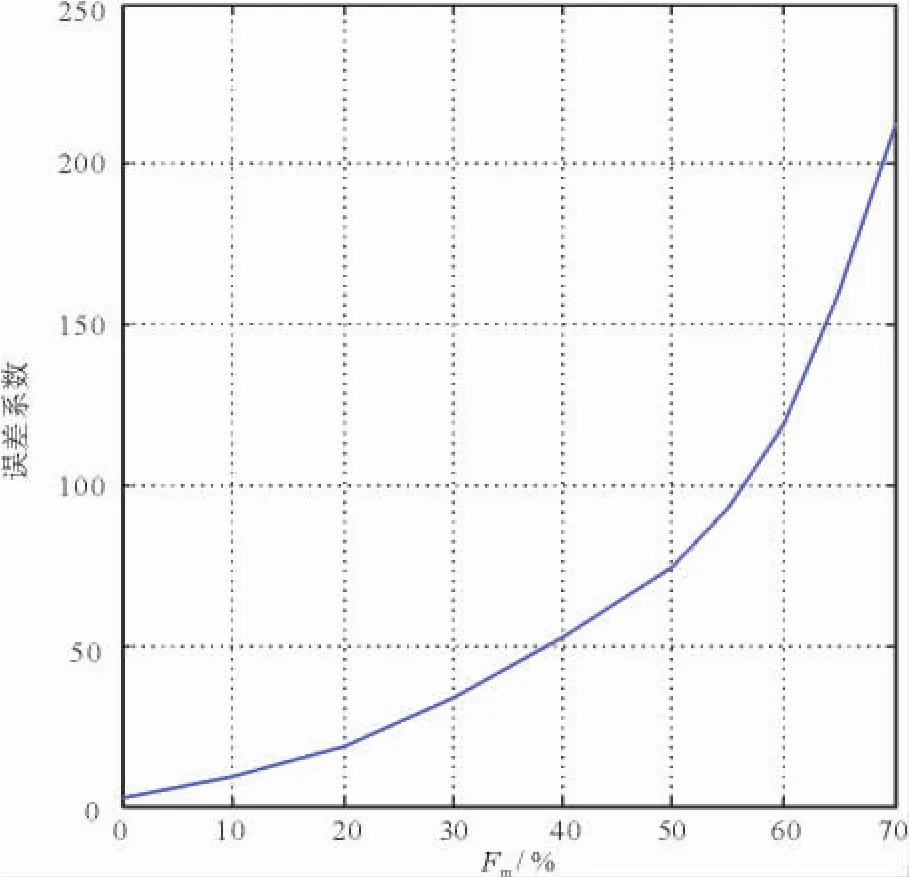
图7 SAIFI误差系数分析

3 结语

传统未考虑气候因素的可靠性评估，其可靠性指标存在一定的误差，可能会影响运行规划人员的决策分析。本文在传统可靠性分析的基础上，考虑极端恶劣气候因素，采用三状态气候模型分析某配电系统可靠性水平，并进行误差分析，以此保证可靠性分析的客观实际性。尤其在目前灾害性气候日益频繁的环境下，在可靠性分析中有必要考虑极端恶劣气候因素的影响，其具有一定的现实意义。

[1]Billinton R,Wu Chenjian.Predictive Reliability Assessment of Distribution Systems Including Extreme Adverse Weathe[C]//Proc.of CCECE,May,2001:719-724.

[2]许树楷，赵杰.电网冰灾案例及抗冰融冰技术综述[J].南方电网技术,2008,2（2）:1-6.

[3]丁军策,苏寅生,李建设,等.冰灾期间电网运行特点及应对措施[J].南方电网技术,2008,2（2）:23-26.

[4]Billinton R,Acharya JR.Weather-Based Distribution System Reliability Evaluation[J].IEE Proc-Gener Transm Distrib,2006，153（5）:499-506.

[5]翟海燕,赵明,李本瑜,等.2008年云南电网抗击冰灾继电保护技术措施[J].南方电网技术,2008,2（2）:40-43.

[6]熊媛,黄新,张薇薇,等.冰灾期间贵阳地区低周减载方案[J].南方电网技术,2008,2（2）:37-39.

[7]Billinton R,Singh GD.Reliability Assessment of Transmission and Distribution Systems Considering Repair in Adverse Weather Conditions[C]//Proc of 2002 CCECE,2002:88-93.

[8]陈永进，任震，黄雯莹.考虑天气变化的可靠性评估模型与分析[J].电力系统自动化，2004,28（21）:17-21.

[9]刘洋，周家启，计及气候因素的大电力系统可靠性评估[J].电力自动化设备，2003,23（9）:60-62.

[10]Billinton R,Allan RN.Reliability evaluation of engineering systems:concepts and techniques[M].New York:Plenum Press,1983.

[11]Billinton R,Allan RN.Reliability evaluation of power systems[M].New York and London:Plenum Press,1984.

[12]郭永基.电力系统可靠性原理和应用[M].北京：清华大学出版社，1985.

[13]Roy Billinton,Janak Acharya.Distribution system reliability assessment incorporating weather effects[C]//Universities Power Engineering Conference,2006，41（1）：282-286.

[14]Roy Billinton,Janak Acharya.Consideration of Multi-state Weather Models in Reliability Evaluation of Transmission and Distribution Systems[C]//Electrical and Computer Engineering,Canadian Conference，2005:916-922.

[15]Billinton R and Singh G.Application of Adverse and Extreme Adverse Weather:Modeling in Transmission and Distribution System Reliability Evaluation.Generation,Transmission and Distribution [C]//IEE Proceedings，Volume 153,2006:115-120.