同时的相对性在长度收缩公式推导中的应用

李 勇，王玉连，刘 慧，郭明磊



同时的相对性在长度收缩公式推导中的应用

李 勇，王玉连，刘 慧，郭明磊

(安徽科技学院 理学院，安徽 凤阳, 233100)

根据洛仑兹变换从不同角度推出长度收缩公式，指出在推导过程中可能会出现的问题，并强调同时的相对性在公式推导过程中的重要性.

洛仑兹变换；同时的相对性；长度收缩

有关狭义相对论中长度收缩公式的推导，大家早已谙熟，各种物理学教材和文献都给出了详细的推导过程[1-4]，但多数都是应用洛仑兹逆变换进行推导的，在推导过程中一般不用考虑同时的相对性，如果应用洛仑兹正变换进行推导，则必须考虑同时的相对性，如果忽略了这一点，推导出的结果可能会跟教材中的结论不一致甚至相反. 本文应用洛仑兹正变换对长度收缩公式进行推导，同时指出在推导过程中不注意同时的相对性可能会出现的问题.

1 同时的相对性

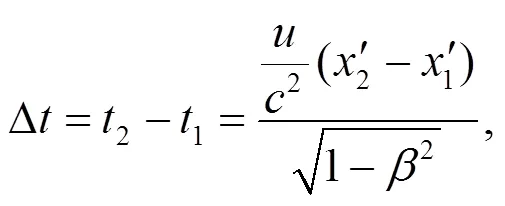
(1)式说明在系中的观察者测得这两个事件是先后发生的.

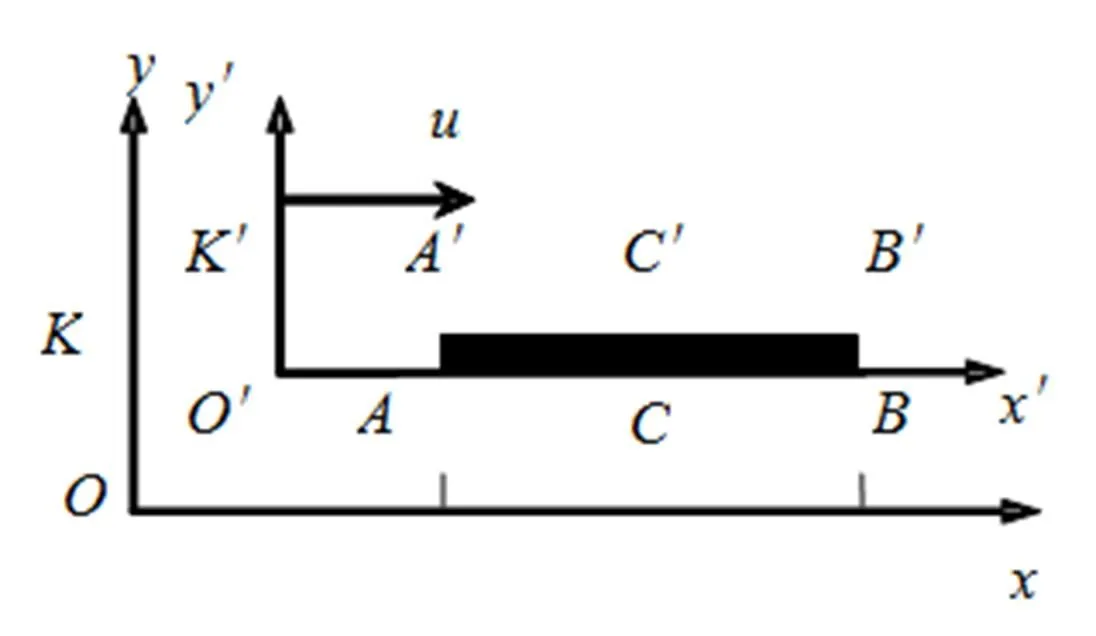
图1 A′B′相对于K系匀速运动

2 长度收缩

图2 AB静止于K系中

两式相减得:

两式相减得:

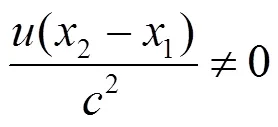
(3)式说明在系中对物体两端的测量是不同时的. 将(3)式代入(2)式中，得到:

即

(5)式说明物体沿速度()方向的运动长度′总比物体固有长度短，这个效应叫做长度收缩. 该结论与文献[1—2]中的结论相同.

由同时的相对性可知，在′系中为同时测量的两个事件变到系中为不同时测量的两个事件，其时间间隔由(3)式表示. 如果我们在推导过程中不注意到这一点，就得不到上述结论. 有人就提出：在系中，由于物体相对观察者静止，对物体两端测量的时间1和2没有任何限制，可以假设1=2，则(2)式简化为：

(8)式的结论与(5)相同，它同样是在′1=′2的条件下推出来的. 由此可见，在推导长度收缩公式时，我们必须明白同时的相对性在推导过程中的地位和作用.

3 结束语

从上述长度收缩公式推导过程来看，应用洛仑兹正变换推导长度收缩公式虽显繁琐，但其中的物理意义较为丰富，特别能帮助学生加深对同时的相对性的理解，有利于培养学生分析问题和解决问题的能力，在教学过程中此方法值得到借鉴.

[1] 程守洙, 江之永. 普通物理学[M]. 5版. 北京: 高等教育出版社, 1998.

[2] 张三慧. 大学基础物理学[M]. 北京: 清华大学出版社, 2003.

[3] 王超群. 关于时间膨胀和长度收缩的研究[J]. 陕西师范大学学报, 2007, 35: 39-41.

[4] 王景雪, 汤正新, 陈庆东, 等. 基于同时的相对性对钟慢尺缩效应的再认识[J]. 大学物理, 2009, 28(10): 24- 27.

Application of relativity of simultaneity in deduction of the formula of length contraction

LI Yong，WANG Yu-lian，LIU Hui，GUO Ming-lei

(College of Sciences，Anhui Science and Technology University，Fengyang 233100，China)

According to Lorentz transformation, The article deduces the formulas of length contraction by different ways, pointing out the problem that may arise in the deductive process, and emphasize the importance of relativity of simultaneity in the deductive process of the formula.

lorentz transformation; relativity of simultaneity; length contraction

O 412.1

A

1672-6146(2010)03-0025-02

10.3969/j.issn.1672-6146.2010.03.009

2010-05-31

安徽省教学研究项目资助(2008jyxm338)

李勇(1975-)，男，硕士，讲师，主要从事大学物理教学.