量子遗传算法在TSP中的应用

潘子宇 耿鹏

南京工程学院通信工程学院 江苏 211167

0 引言

近年来，启发式智能优化方法越来越引起人们的关注。如：模拟退火、遗传算法、蚁群算法等，它们是解决NP问题的有效工具。

量子计算作为计算机科学界一个新兴的研究领域，在过去的几年里一直是人们研究和探索的热点问题。由于量子计算的并行性可以大大地降低了算法的复杂度，所以被广泛地用于解决需要大量计算空间的复杂问题。

1 量子遗传算法

量子遗传算法（QGA）建立在量子的态矢量表述的基础上，将量子比特的几率幅表示应用于染色体的编码，使得一条染色体可以同时表达多个状态的叠加，并利用量子旋转门的调整和量子非门来实现染色体的更新操作，从而实现了目标的优化求解。

1.1 量子比特编码

在量子计算机中，充当信息存储单元的物理介质是一个双态量子系统，我们称之为量子比特。量子比特与经典位的不同之处就在于它可以同时处在两个量子态的叠加态之中。

在量子遗传算法中，采用量子比特的存储和表达一个基因。该基因可以为一个“0”态或“1”态，或它们的任意叠加态。即该基因所表达的不再是某一确定的信息，而是包含所有可能的信息，对该基因的任一操作也会同时作用于所有可能的信息。

1.2 量子遗传算法流程

量子遗传算法的算法流程具体如下：

① 初始化种群Q（t0）；

② 对初始化种群中的各个体实施一次测量，得到一组状态P（t0）；

③ 对各状态进行适应度评估；

④ 记录下最佳个体状态及其适应度值；

⑤ while非结束状态do

begin

t=t+1；

对种群Q（t）实施一次测量，得到一组状态P（t）；

对各状态进行适应度评估；

依据一定的调整策略，利用量子旋转门U（t）和量子非门对种群进行更新，得到子代种群Q（t+1）；

记录下最佳个体状态及其适应度值。

End

1.3 量子旋转门调整策略

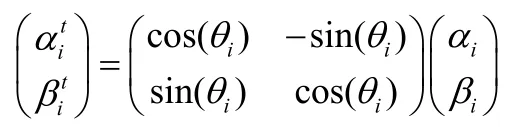
作为演化操作的执行机构，量子门可根据具体问题进行选择。目前已有的量子门有很多种，根据量子遗传算法的计算特点，选择量子旋转门较为合适。量子旋转门U（t）的调整操作如下式所示：

量子遗传算法中，旋转门是最终实现演化操作的执行机构。其调整策略如表1所示。

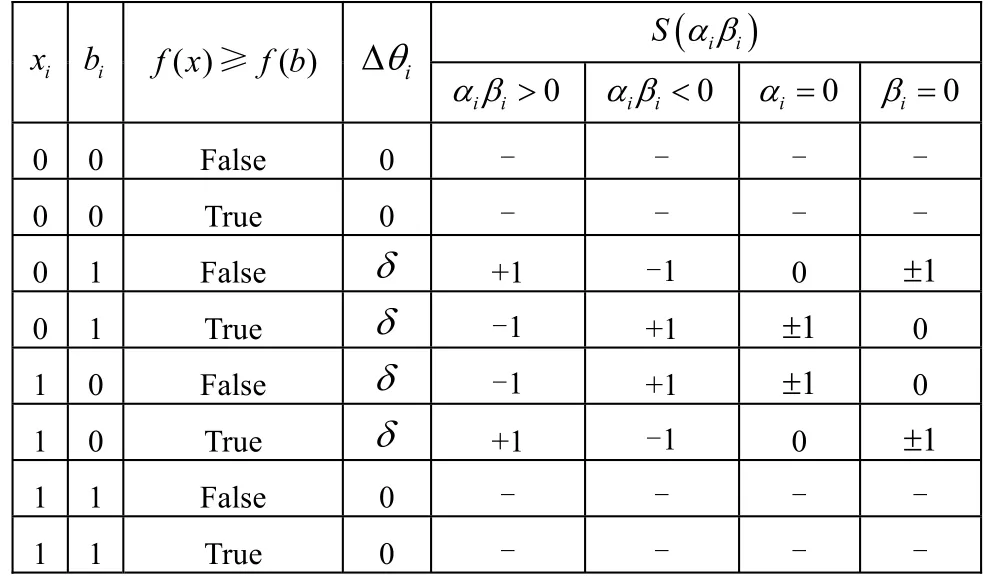
表1 旋转角选择策略

旋转角的选择可以通过静态或动态的方法调整。在表1中，δ为每次调整的角步长。δ值的选择对算法的效率也有着很大的影响，δ的值太大可能会使结果发散或早熟收敛到局部最优解。实验结果表明：动态调整旋转角策略的收敛速度优于固定旋转角策略。

1.4 量子变异

变异的作用主要在于阻止未成熟收敛同时提供算法的局部搜索能力。变异的方法有许多种。具体操作方法如下：

（1）以一定的概率Pm从种群中随机选取若干个个体；

（2）对选种的个体按照一定的概率随机确定一个或多个变异位；

（3）对选中位的量子比特的几率幅执行量子非门操作（“0”变“1”，“1”变“0”），即完成了该量子比特的变异操作。

量子变异操作实际上是改变了该量子比特态叠加的状态，使得原来倾向于坍缩到状态“0”的变为倾向于坍缩到状态“1”，或者相反。显然，这样的变异操作对染色体的所有叠加态均同时有效。

2 算法实现与性能分析

2.1 旅行商问题的数学描述

旅行商问题的数学描述十分简单，该问题的约束条件只有一个，就是路程。因此，我们的目标就是搜索整数子集（X中的元素表示对n个城市的编号）的一个排列使

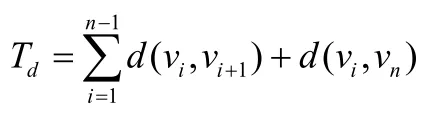
2.2 基于量子遗传算法的TSP问题求解

运用量子遗传算法求解TSP问题的算法流程图（如图1）。

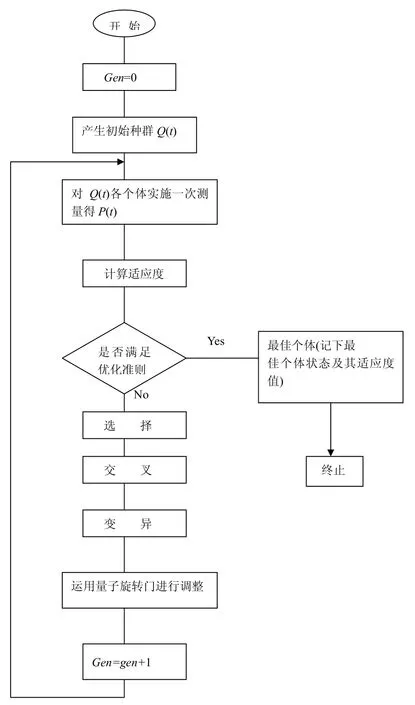
图1 量子遗传算法流程图

2.3 仿真实验与结果分析

（1）量子遗传算法和遗传算法求解TSP问题的比较

在实验过程中，我们采用相同的编码原则，相同的适应度函数，相同的交叉概率、变异概率。分别对5、7、9城市的运行结果作了比较，如表2所示。

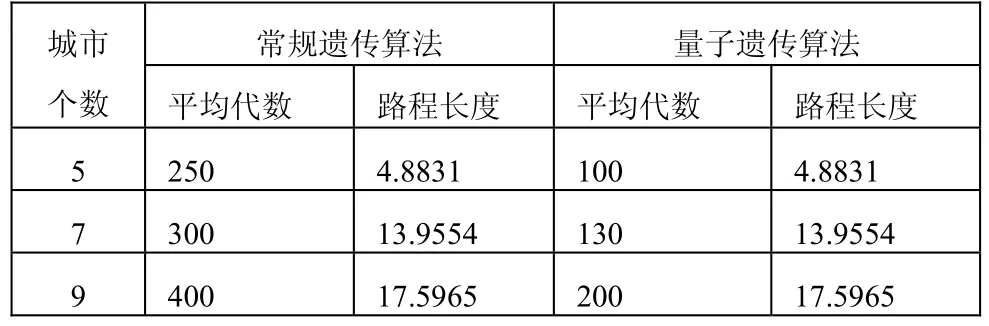
表2 量子遗传算法和遗传算法的结果

从上表中我们可以看出，遗传算法和量子遗传算法均能收敛到最优解。但量子遗传算法花费的迭代数目明显小于常规遗传算法。

（2）算法中静、动态旋转角调整的结果比较

对两种方法分别进行了20、50、100次的循环迭代，其中在动态调整策略中，针对角步长δ的确定方案，我们在现有的指数函数调整策略的基础上提出了基于正弦函数的调整策略，并比较了这两种动态调整策略的性能。我们采用搜索成功率作为调整策略比较的标准。得到的结果如表3所示。

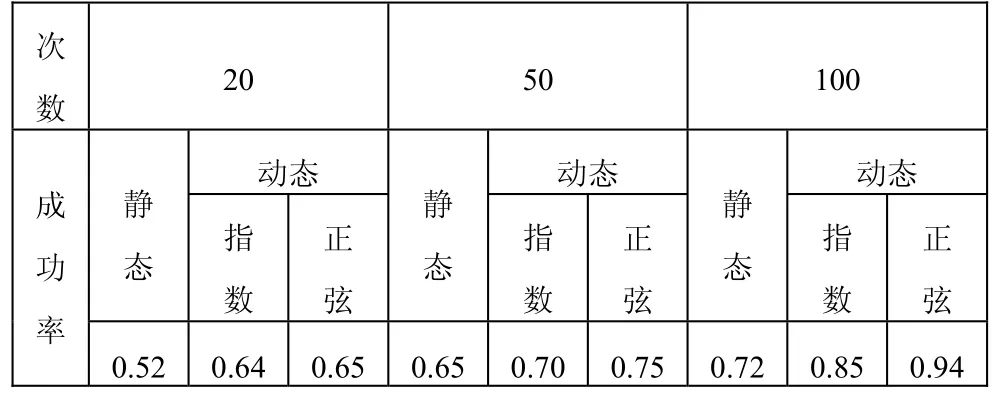
表3 静、动态旋转角调整的结果

由于δ的值太小将影响收敛速度；太大可能会使得结果发散，或早熟收敛到局部最优解。因此使用动态旋转门调整可以得到更为理想的结果。此外在实验中我们还发现，动态调整策略的收敛速度也比静态调整策略来的快，其最终结果的收敛性也比静态调整策略来的好，静态策略的最终结果较为发散。从表中我们还可以看出，随着叠代次数的增加，动态调整策略的优势越来越明显。

此外，我们还将现有的指数函数和我们提出的正弦函数两种不同的动态调整策略作了比较，其中指数调整策略的函数为，正弦调整策略的函数为通过实验，我们可以看出，以正弦函数作为δ的调整策略取得了比指数函数更好的效果。

3 总结与展望

本文提出了改进的量子遗传算法，应用正弦函数动态调整量子旋转门，有效地克服了现有量子旋转门调整方案的不足，避免了算法过早陷入局部最优解。对目前组合优化问题中的代表性问题——旅行商问题（TSP）的仿真实验表明，改进算法的优化质量和效率都优于遗传算法和一般量子遗传算法。

接下来，我们还将进一步研究算法的各个参数，以便提高算法的性能。我们还将设法把这一算法应用到其他组合优化问题中。

[1]杨俊安，庄镇泉.量子遗传算法研究现状[J].计算机科学.2003.

[2]王凌，吴昊，唐芳.混合量子遗传算法及其性能分析[J].控制与决策.2005.

[3]杨淑媛，刘芳，焦李成.一种基于量子染色体的遗传算法[J].西安电子科技大学学报.2004.

[4]李英华，王宇平.有效地混合量子遗传算法[J].系统工程理论与实践.2006.