海岸带土地利用模拟结果对元胞邻域的响应研究

冯永玖，韩 震

（上海海洋大学 海洋科学学院，上海201306）

近年来，随着人们对复杂系统动态演变过程的关注，元胞自动机模拟及其作用越来越受到重视。元胞自动机（Cellular Automata，CA）最早由美国数学家Ulam在19世纪40年代提出，是一种在时间和均离散的系统。元胞自动机具有“自下而上”的结构，通过简单的底层交互行为，能够反映全局系统的复杂行为及其变化。1984年英国数学家Wolfram在Nature发表文章认为，CA可以用于复杂系统的模拟，并给出了元胞自动机的定义、构成元素以及转换规则等［1］。此后，CA应用研究领域剧增，在计算机、生态、交通、地理等领域得到了较为广泛的应用。尤其在城市扩展演变与复杂土地利用变化方面，利用元胞自动机模拟方法不仅能够重建历史动态变化过程［2－3］，而且能够根据不同的条件预测未来发展的可能情景［4－5］。作为复杂地理空间实体，城市与土地从上一时刻向下一时刻的转变依据的是元胞的转换规则（Transition Rules），这种规则是建立元胞自动机模型的核心［6］。一般地，转换规则由元胞邻域、区域影响变量、限制因素和随机变量等组成。大部分研究均把重点放在区域变量如何影响地理实体的演变，从而得到合理的元胞转换规则作为研究的重点［2－5］。但是，随着规划和决策对模拟精度的要求越来越高，模拟结果的精度和不确定性开始受到重视［7－9］。

元胞自动机模拟结果是产生一系列模拟和预测情景，这些结果是与基准图件相似的数据和图件，CA模型有明显的空间尺度依赖性，不可避免地存在误差和不确定性［10］。叶嘉安等从数据源、数据转换、CA模型系统（包括转换规则、邻域结构、模拟时间和随机变量）等方面探讨了CA模拟的误差传递与不确定性问题［11］；Liu研究了元胞尺度大小对城市土地利用模拟结果的精度影响［12］；Moreno等从CA模型的空间尺度依赖性出发，提出了通过不规则元胞组合的改进方法［10］。

大量研究证实，元胞的空间尺度及组合不仅影响土地利用变化的模拟结果，甚至影响规则的挖掘与获取，及不同邻域组合下，得到的CA转换规则、设置的转变阈值及模拟结果（包括数量、空间位置及形态）均有较大差异。可见，元胞邻域的大小及其组合是CA土地利用模拟不可忽视的一环。本文重点讨论探讨元胞邻域的大小及组合对模拟过程和结果的影响，并通过海岸带土地利用变化模拟的案例进行实证研究。

1 地理元胞自动机

1.1 基本原理

在CA模型中，散布在规则格网（Lattice）中的每一个元胞取有限的离散状态，遵循统一的转换规则，依据确定的局部规则作同步更新［1］。CA的四个基本要素为元胞、状态、邻域以及转换规则，而其它非基本要素则包括元胞空间和时间［1］。元胞（Cell）是元胞自动机最基本的组成部分；状态（State）是每个元胞拥有的（多个）状态变量；邻域（Neighbor）是指中心元胞周围的一组元胞，研究中通常采用Moore型或扩展Moore型邻域；规则（Rule）是元胞当前状态转换到下一时刻所应遵循的转换条件（Transition Function）。

1.2 元胞邻域

（1）Moore 3×3邻域（普通 Moore邻域）。一个元胞的上下、左右、左上、右上、左下及右下的8个元胞为其邻域，其数学定义如式（1）［13］。

（2）Moore 5×5邻域。把 Moore型的邻域半径扩展为2，扩展后的邻域数为24，其数学定义如式（2）［13］。

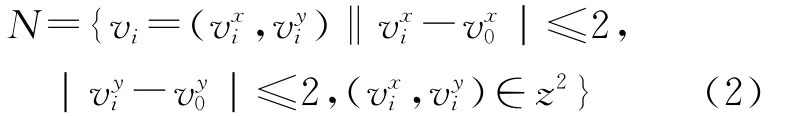
（3）Moore 7×7邻域。把 Moore型的邻域半径扩展为3，邻域数为48，其数学定义如式（3）［13］。

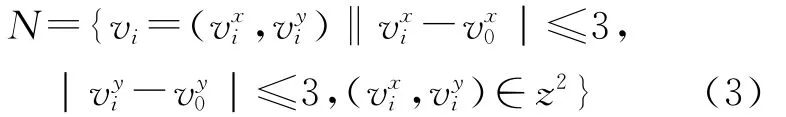
图1 常见的几种Moore元胞邻域定义

1.3 CA转换规则

一般地，利用CA对海岸带土地利用进行模拟，其核心是转换规则的确定。而本研究不考虑转换规则的影响，重点分析元胞邻域数量对于模拟结果的影响，以分析使用哪一种元胞类型较为适合。在此条件下，每个元胞在下一时刻能够发生状态转变的概率可以用式（4）表达。

模拟之前，设置元胞是否可以发生转变的阈值Pthreshold，当＞Pthreshold则发生转变，否则元胞保持原状态不变。

2 模拟结果对元胞邻域的响应分析

2.1 研究区域及模拟结果

为测试不同元胞组合对模拟结果的影响，选择上海市浦东新区海岸带某区域作为研究对象。现浦东新区由原浦东和南汇于2009年合并而成。原南汇作为上海远郊区，其海岸带土地利用类型复杂多样，包括城市建设、工业开发、垃圾填埋场、城市绿化、大型主题公园、农业基地、滨海湿地等。本文研究区位于南汇沿海区域，面积为90km2

利用GIS组件ArcGIS Engine 9.3在VS2005环境下开发海岸带土地利用模拟模块，通过改变元胞邻域，产生一系列模拟结果（见图2）。模拟中，将土地利用类型简化为3类：分别为已开发土地、未开发土地和水域；运行的阈值为0.52，模拟运行次数为60。

2.2 模拟结果分析

由于水域作为限制条件，因此模拟中其元胞状态保持不变，发生变化的元胞为已开发和未开发的元胞，结果是已开发的元胞数量不断增加、未开发的元胞数量不断减少，故而检测模拟结果对元胞邻域的响应只需要检测已开发或未开发的元胞数量即可。本研究把已开发的元胞作为研究的重点。对于图2的目视检测和直观认识可知，3种元胞邻域产生的模拟结果在数量上和形态上均有较大差异。初始状态，已开发的元胞数量为14 753；而3种不同邻域下模拟运行1～60次产生的元胞数量如表1所示。

图2 基于3种不同的Moore邻域的模拟结果

表1 三种不同元胞邻域模拟结果趋势分析

图3 三种不同元胞邻域模拟结果趋势分析

从表2可知，Moore 3×3和Moore 5×5邻域分别模拟运行到15和25次时不再发生变化，而Moore 7×7邻域在60次运行以内均发生变化。图3显示了模拟次数与模拟最终状态已开发的元胞数量之间的关系，从模拟过程变化曲线可知，Moore 3×3与Moore 5×5相似，而与Moore 7×7的差异较大，其中Moore 3×3模拟变化甚微，Moore 5×5变化次之，而Moore 7×7模拟结果变化显著。Moore 3×3和Moore 5×5在1～10次模拟运行元胞增加数量显著，分别增加元胞数量为1 224和2 633个，10次之后趋于缓慢，分别增加元胞数量22和143个；Moore 7×7在1～20次模拟运行增加元胞数量8 423个，20次之后趋于缓慢，增加元胞数量4 185个。

综上所述，可归纳不同元胞邻域下海岸带土地利用模拟结果的特点：①从数量上看，模拟初期已开发元胞增加显著，随着模拟次数增加已开发元胞数量增加趋缓，邻域范围越小导致模拟结果越早停止变化，这是因为大邻域范围综合了区域发展的更多因素，而小邻域范围只考虑了中心元胞周围的局部因素。②从形态上看，元胞邻域范围越大模拟结果真实性越低，凡是包含在邻域范围内的元胞，随着模拟次数增加，其状态均有可能改变，而当邻域范围越大，可以改变状态的元胞则越多，因此一些包围在已开发的元胞区域中的未开发元胞，虽然实际中并未得到开发，但是其状态却发生了改变，从图2看这种情况在Moore7×7邻域中比较明显。③从不确定性方面来看，小邻域范围由局部元胞组成，而大邻域范围由较大区域的元胞组成，显然邻域范围越大、因素越多，则模拟不确定性增加。可见，小邻域范围模拟结果形态真实、不确定性较低，但会导致模拟运行变化过早终止；而大邻域范围模拟运行变化延续性较强，但是模拟结果形态欠缺真实、不确定性增加。

因此，在海岸带土地利用模拟过程中必须依赖全局变量，而不是邻域范围变量。由于各种尺度邻域范围具有自身的优缺点，邻域范围大小及其组合的选择必须考虑研究区域的特点、全局变量的情况，利用试错法进行模拟并评价精度，最后确定模拟案例的特征尺度及较优的邻域大小及组合。

3 结论

元胞自动机是一种“自下而上”的离散系统，能够模拟复杂现象和系统的演变过程并预测其未来情景。海岸带土地利用变化模拟是CA的重要应用领域。研究表明：元胞邻域的大小及其组合对海岸带土地利用模拟结果有显著影响。通过测试分析3种不同的Moore邻域对模拟结果的影响，初步研究了模拟结果对元胞邻域的响应特征。

研究证实：元胞邻域对模拟结果在3个方面有重要影响，分别是元胞数量、空间形态及不确定性。针对一般性模拟研究，无法判断什么样的元胞尺度及组合对海岸带土地利用模拟时最优的，必须结合实际模拟案例，考虑组成元胞全局转换规则的因素，在多次模拟比较之下，才能够确定最佳元胞邻域尺度和组合。此外，本研究的结论对不仅对海岸带土地利用变化模拟适用，而且对其他类型的空间演变模拟及预测均有参考价值。

［1］ Wolfram S.Cellular Automata as Models of Complexity［J］.Nature，1984，311（10）：419－424.

［2］ Al－kheder S，Wang J，Shan J.Fuzzy inference guided cellular automata urban－growth modelling using multitemporal satellite images ［J］.International Journal of Geographical Information Science，2008，22（11）：1271－1293.

［3］ Liu Xiaoping，Li Xia，Liu Lin，et al.A bottom－up approach to discover transition rules of cellular automata using ant intelligence ［J］.International Journal of Geographical Information Science，2008，22（11）：1247－1269.

［4］ 何春阳，史培军，陈晋，等.基于系统动力学模型和元胞自动机模型的土地利用情景模型研究［J］.中国科学（D辑）：地球科学，2005，35（5）：464－473.

［5］ 黎夏，杨青生，刘小平.基于CA的城市演变的知识挖掘及规划情景模拟［J］.中国科学（D辑）：地球科学，2007，37（9）：1242－1251.

［6］ Wu F.Calibration of stochastic cellular automata：the application to rural－urban land conversions［J］.International Journal of Geographical Information Science，2002，16（8）：795－818.

［7］ 张杰，周寅康，李仁强，等.土地利用／覆盖变化空间直观模拟精度检验与不确定性分析：以北京都市区为例［J］.中国科学（D辑）：地球科学，2009，39（11）：1560－1569.

［8］ Robert Gilmore Pontius，Neeti Neeti.Uncertainty in the difference between maps of future land change scenarios［J］.Sustainable Science，2010，5：39－50.

［9］ Lien Poelmans，Anton Van Rompaey.Complexity and performance of urban expansion models［J］.Computers，Environment and Urban Systems，2010，34（1）：17－27.

［10］ Moreno Niandry，Wang Fang，Danielle J.Implementation of a dynamic neighborhood in a land－use vector－based cellular automata model［J］.Computers，Environment and Urban Systems，2009，33：44－54.

［11］ Yeh Anthony Gar－On，Li Xia.Errors and uncertainties in urban cellular automata ［J］.Computers，Environment and Urban Systems，2006，30：10－28.

［12］ Liu Yan.The impact of neighbourhood size on the accuracy of cellular automata－based urban modelling ［J］.Applied GIS，2007，3（5）：1－14.

［13］ 徐昔保.基于GIS与元胞自动机的城市土地利用动态演化模拟与优化研究：以兰州市为例［D］.兰州：兰州大学，2007.