基于变换空间近邻图的自助型局部保持投影

乔立山1,2 张丽梅1,2 孙忠贵2

(1.南京航空航天大学计算机科学与工程系,南京,210016,中国;2.聊城大学数学科学学院,聊城,252000,中国)

INTRODUCTION

In practice,the high-dimensional data are often utilized such as face images and gene expression micro-arrays. Dimensionality reduction(DR)is a principle way to mine and understand such high-dimensional data by mapping them into another(usually low-dimensional)space.Classical DR methods include PCA,ICA and LDA,and so on[1].However,these methods cannot discover the nonlinear structure in data.To address this issue,in the past decade,researchers have developed many nonlinear manifold learning algorithms such as LLE[2],ISOM AP[3]and Laplacian eigenmaps[4].They give more flexibility in data modeling,but generally suffer from high computational cost and the so-called″out-of-sample″problem.Ref.[5]showed that although such nonlinear techniques perform well on selected artificial data sets,they generally do not outperform the traditional PCA on real-world tasks yet.

In the recent years,there is an increasing interest in linearized locality-oriented DR methods,e.g., the locality preserving projections(LPP)[6],the neighborhood preserving embedding (NPE)[7],the unsupervised discriminant projection(UDP)[8],and the sparsity preserving projections(SPP)[9],etc..On one hand,these algorithms are linear in nature,thus avoiding the″out-of-sample″problem involved in nonlinear manifold learning.On the other hand,they model the local neighborhood structure in data,and generally achieve better performance than typical global linear methods such as PCA.According to Ref.[10],almost all of the existing locality-oriented methods essentially share the similar objective function yet with different well-constructed neighborhood graphs.Therefore,without loss of generality,LPP in virtue of its popularity and typicality is chosen to develop the algorithm and demonstrate the idea,though the idea in this paper can be easily and naturally extended to other locality-oriented DR methods.

As a representative of locality-oriented DR algorithms,LPP has been widely used in many practical problems,such as the face recognition[11].Despite its unsupervised nature,LPP has potential discriminative power by preserving the local geometry of data.However,the neighborhood graph underlying LPP is defined(Eq.(2))based on original data points,and must be fixed all along once constructed.As a result,the performance of LPP generally relies heavily on how well the nearest neighbor criterion work in original space[12].In addition,the so-defined neighborhood graph suffers seriously from the difficulty of parameter selections,i.e.,the neighborhood size k and the Gaussian kernel widthe.

To address these problems,this paper proposes a novel DR algorithm,called the self-dependent LPP(sdLPP),which is based on the observation that the nearest neighbor criterion usually works well in LPP transformed space.Firstly,LPP is performed based on the typical neighborhood graph.Then,a new neighborhood graph is constructed in LPP transformed space and repeats LPP.Furthermore,a new criterion called the improved laplacian score is developed as an empirical reference for discriminative power and iterative stop condition.Finally,experiments on several publicly available UCI and face data sets verify the feasibility and the effectiveness of the proposed algorithm with promising results.

1 BRIEF REVIEW OF LOCALITY PRESERVING PROJECTIONS

Given a set of data pointsX= [x1,x2,…,xn],xi∈Rd,LPP aims at seeking a set of projection directions by preserving the local geometric data structure.The objective function of LPP is defined as follows

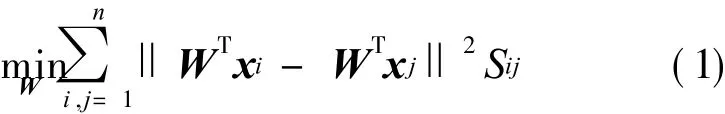
whereW∈ Rd×d′(d′＜d)is the projection matrix and S= (Sij)n×nthe adjacency weight matrix defined as

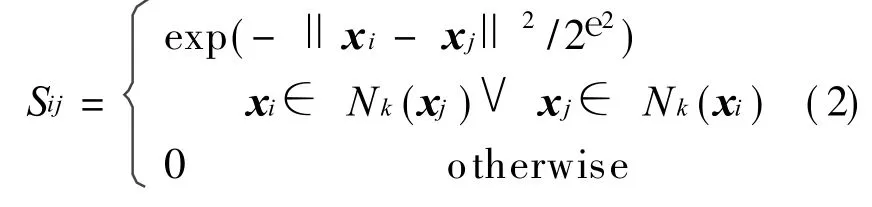
where Nk(xj)is k nearest neighbors of xj.

To avoid degenerative solution,this paper,where diiis the

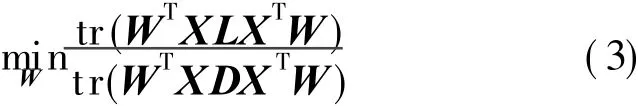
where D=diag(d11,d22,…,dnn)is a diagonal matrix and L=D-S the graph Laplacian[6].Eq.(3)is a typical non-convex[13],and it is often solved approximately by the generalized eigenvalue problem:XLXTw=λ XDXTw,where w is the eigenvector for constructing.row sum of S(or column since S is symmetrical).Then, with simple formulation, LPP can be rewritten as a compact trace ratio form[6]

2 SELF-DEPENDENT LOCALITY PRESERVING PROJECTIONS

2.1 Motivation

According to Refs.[6,14],the locality preserving power of LPP is potentially related to discriminating power.As a result,the 1-NN classifier in LPP transformed space generally achieves better performance in comparison with the baseline scenario(i.e.,performing 1-NN classifier in original space without any transformation).In fact,this is also the observation from the experiments in many research work[6,9,14]related to LPP.

Since the neighborhood graph and 1-NN classifier are both closely related to the nearest neighbor criterion,a natural idea is that the neighborhood graph constructed in the LPP transformed space includes more discriminative information than the one constructed in the original space.Therefore,this paper updates the neighborhood graph in previous LPP transformed space,and then repeats LPP.The corresponding algorithm is called the self-dependent LPP(sdLPP),since it only depends on LPP itself instead of resorting to other extra tricks or tools.This paper develops an improved Laplacian score(LS)as an alternative under the stop condition,and proposes a specific algorithm.

2.2 Improved Laplacian score

The original Laplacian score(LS)is introduced to scale the importance of the feature(or variable)[15]. Different from classical Fisher score[16]which can only work under supervised scenario,LS can work under supervised,unsupervised and even semi-supervised scenarios.Although LS aims at the feature selection,it can naturally be extended to the feature extraction or the dimensionality reduction field.However,typical LS is based on the artificially predefined neighborhood graph,and it becomes a constant once the specific projection directions are given.So the reliability of LS relies heavily on the single pre-fixed neighborhood graph;and LS cannot directly be used as iteration termination condition in the proposed algorithm.

An improved Laplacian score(iLS)is defined as follows

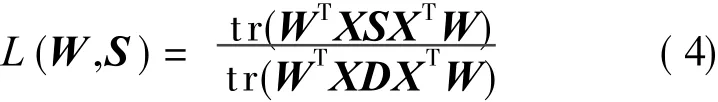
The i LS shares the similar mathematical expression to the objective function of Eq.(3)and typical LS[15],but it has remarkable differences from them.In typical LS(or more generally,the most existing locality-oriented DR algorithms),the adjacency weight matrix S of the graph is fixed in advance.While in the proposed iLS,S is variable,that is,the iLS is a joint function with respect to W and S.

2.3 sdLPP Algorithm

Based on the above discussion,sdLPP algorithm is given as follows:

(1)As in LPP and other locality-oriented DR algorithms,the data points in a PCA transformed subspace are firstly projected to remove the null space of XXTand the possible singularity problem is avoided.Without loss of generality,X is used to denote the data points in the PCA transformed subspace.

(2)Constructing initial neighborhood graph G(X,S)with appropriate neighborhood parameter k and Gaussian kernel width ein Eq.(2),then calculating the projection matrix W by solving the generalized eigenvalue problem: XLXTw =λ XDXTw,and finally calculating the iLS,Lold=L(W,S)with current W and S.

(3)Updating S in the previous LPP transformed space with the same parameters k ande,then repeatly computing the new projection matrix W and i LS,Lnew=L(W,S)with the new W and S.

(4)If Lnew＞Lold,let Lold= Lnewand turn to Step(3),otherwise,break and return to W.

It is easy to see that the sdLPP algorithm is simple.Here,it needs to point out that iLSis not an accurate indicator of the discriminate power,since the proposed algorithm completely works under the unsupervised scenario.Therefore,in the experiments,this paper first performs ten iterations and judges whether they should be continued according to iLS at another ten iterations.This trick is used to avoid the unexpected stop due to the possible fluctuation of iLS.Of course,a well-designed heuristic strategy is worthy of deep study in the future.

3 EXPERIMENTS

In this section,the algorithm is compared with LPP through the illustrative example,the clustering and the face recognition experiments.

3.1 Illustrative example

Firstly,this paper visually show how and why the algorithm works on the widely used Wine data set from the UCI machine learning repository.The Wine has 13 features,3 classes and 178 instances.A main characteristic of this data set is that its last feature has large range and variance relative to other ones.As a result,such remarkable feature will play a key role in the data distribution.This generally challenges the typical locality-oriented DR methods including LPP,since the neighborhood graph is fixed in advance and heavily depends on the last remarkable feature due to its large range and variance in the original space.

(1)Data visualization

In particular,Fig.1(a)shows the 2-D projections of Wine by the typical LPP whose adjacency graph is constructed with neighborhood size k=min{n1,n2,n3}- 1,where niis the sample number from the i th class,and heat kernel widtheas the mean norm of the data[17](the influence of these parameters on the ultimate performance is discussed.).By the LPP transformation,the three classes are overlapped together.Then,the proposed sdLPP is performed.Fig.1(b)shows the improved Laplacian score at each iteration.Generally speaking,it presents an increasing tendency with the iteration.Figs.1(c-f)give the 2-D projections by sdLPP after 1,5,10,and 20 iterations,respectively,which show that the three classes in the subspace are gradually separated from each other.This illustrates that the graph updating strategy can potentially benefit the subsequent learning task.

Fig.1 Data visualization results and iLS of sdLPP at each iteration on Wine data set

(2)Sensitivity to parameters k ande

The model selection for unsupervised learning is one of classical challenges to machine learning and pattern recognition tasks.Fig.2 shows the performances of LPP and sdLPP on Wine data set with different parameter values,respectively.In the experiment,25 samples per class are randomly selected for training and remaining for test.Then,the classification accuracies of 20 training splits per test are averaged,and the best results at certain dimensions are plotted.In particular,Fig.2(a)shows the classification accuracies using graphs with the different neighborhood size k and fixed heat kernel widthe0,where k is traversed from 1 to 50 ande0is set as the mean norm of the training samples[17].Fig.2(b)shows the accuracies using graphs with different kernel width e and fixed k,where e is chosen from{2-10e0,…,20e0,…,210e0}and k is set to 24,i,e.,25-1.

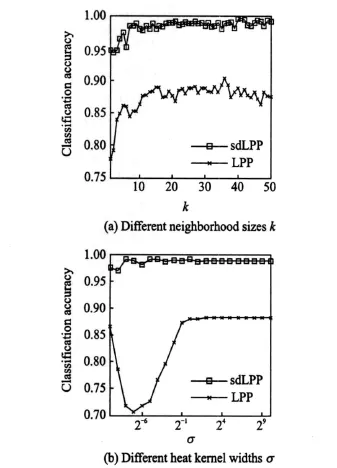
Fig.2 Classification accuracies on Wine using graphs

As shown in Fig.2,with the pre-fixed graph,typical LPP generally suffers from serious performance drop if it gives an improper parameter value.In contrast,sdLPP is not so sensitive to the setting of the initial parameters due to the fact that the graph becomes better with the subsequent updating process.

3.2 Clustering

In what follows,this paper performs clustering experiments using ten data sets by widely used UCIincluding Iris,Wine,Wdbc,and so on.The statistical parameters of all the data sets are summarized in Table 1.

Table1 Statistical parameters of used data sets for clustering

In the experiments,the normalized mutual information(NMI)[17]is adopted to evaluate the clustering performance.NMI measurement is defined as

where A and B are the random variables of the cluster memberships from the ground truth and the output of clustering algorithm,respectively;I(A,B)is the mutual information between A and B.H(A)and H(B)are the entropies of A and B,respectively.

On all the data sets,the k-means clustering is performed in the original space(baseline),the LPP transformed space and the sdLPP transformed space,respectively.For LPP and sdLPP,the neighborhood size k is set to min{n1,n2,…,nc},where niis the training sample number from the ith class;the heat kernel parametereis set as the mean norm of the training samples according to the scheme used in Ref.[17].This paper repeats 50 experiments and reports the mean performances and the corresponding subspace dimensions in Table 2.

Table 2 Performance(NMI)comparisons for clustering task

The results show that:(1)the performance of k-means can generally be improved after DR,i.e.,on data sets①—⑤⑧⑨,which illustrates that the locality preserving power is potentially related to discriminative power;(2)on very few data sets(sets⑥⑦),the DR algorithms do not help the clustering,which is due to serious overlap of the data or inappropriately assigned param-eter values for the neighborhood graph;(3)the sdLPP algorithm can remarkably outperform typical LPP on most of the data sets.This illustrates that the neighborhood graph updating can potentially benefit the subsequent discriminant task.

3.3 Face recognition

Typical LPP has been successfully used in the face recognition where it is appeared as the popular Laplacianface[11].This paper experimentally comparesthe proposed algorithmswith Laplacianface on two publicly available face databases:AR and extended Yale B.

(1)Database description

In the experiments,a subset of the AR face database provided and preprocessed by Martinez[18]is used.This subset contains 1 400 face images corresponding to 100 person(50 men and 50 women),where each person has 14 different images with illumination change and expressions.The original resolution of these image faces is 165×120. For the computational convenience,this paper resizes them to 33× 24.Fig.3(a)gives 14 face images of one person taken in two sessions with different illuminations and expressions.Extended Yale B database[19]contains 2 414 front-view face images of 38individuals.For each individual,about 64 pictures are taken under various laboratory-controlled lighting conditions.In the experiments,this paper uses cropped images with resolution of 32×32.Fig.3(b)gives some face images of one person from this database.

(2)Experimental setting

For AR database,the face images taken in the first session are used for training,and the images taken in the second session are used for test;for extended Yale B,this paper randomly selects l(l=10,20 and 30,respectively)samples for training and remaining for test.The ultimate performance is the mean of 10 training per test splits.

Firstly,the data is projected in a PCA transformed subspace,which is calculated using the training samples and kept 98% energy;then,LPP and sdLPP are performed in the subspace,and 1-NN classifier is chosen due to its simplicity,effectiveness and efficiency to evaluate the recognition rates on the test data.As a Baseline,the recognition rates of 1-NN classifier are also given on the raw data.

Fig.3 Face images of one person

(3)Parameter selection

For LPP and sdLPP,the model parameters include the neighborhood size k and the kernel widthe.In our experiments,we empirically sete as the mean norm of the training samples[17],and determine k values by searching in a large range of candidate values and reporting the best results.

(4)Experimental results and discussion

Fig.4 shows the recognition rate curves of different methods on AR and extended Yale B(l=10)databases.For AR,the best recognition rates of Baseline,LPP and sdLPP are 74.57%,79.00% and 81.71%,respectively,where the best neighborhood size k= 1.For extended Yale B,the best performances and corresponding dimensions are reported in Table 3.For l=10,20 and 30,the best neighborhood size k is 1,1 and 2,respectively.

From the experimental results,the following observations are obtained:

Table3 Performance comparisons on extended Yale B database

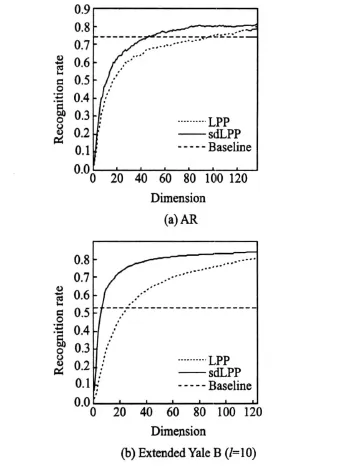
Fig.4 Recognition rate curves based on different methods

(1)Typical LPP and the proposed sdLPP can achieve betterperformance than the baseline method.This further illustrates that the locality preserving DR algorithms can encode potential discriminating information,even though under the unsupervised scenario.

(2)The proposed sdLPP consistently outperforms LPP on the used face databases.This illustrates that sdLPP actually benefits from the graph updating process.

4 CONCLUSIONS

This paper develops a novel LPP algorithm with the adjustable neighborhood graph.As a summary,several favorable properties of the algorithm are enumerate.

(1)sdLPP is self-dependent.It does not acquire to pay incidental expenses for exploiting new tools,but directly work on off-the-shelf LPP.So sdLPP is very simple and analytically tractable.And sdLPP naturally inherits some good characteristics from original LPP.For example,it can avoid the″out-of-sample″problem involved in manifold learning.

(2)sdLPP is not so sensitive to neighborhood size k and Gaussian kernel width erelative to typical LPP,due to the fact that the neighborhood graph becomes better and better in the subsequent updating process.

(3)sdLPP can potentially use the discriminative information lying in both the original space and the transformed space,since the graph in sdLPP is adjustable instead of being fixed beforehand as in LPP.This can potentially help the subsequent learning task.

(4)The idea behind sdLPP is extremely general.It can easily and naturally be applied to many other graph-based DRs just through slight modifications.

It is worthwhile to point out that the proposed algorithm including the improved Laplacian score is completely unsupervised.Although unsupervised DR methods do not require the efforts of human annotators,reliable supervised information generally help to achieve better discriminative power.In the future,we expect to further improve the proposed algorithm by absorbing possibly known label information and extend it to semi-supervised scenario.

[1] Hastie T.The elements of statistical learning:data mining,inference,and prediction [M].2nd Ed.New York:Springer,2009.

[2] Roweis S T,Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323-2326.

[3] Tenenbaum J B,Mapping a manifold of perceptual observations [C]//Neural Information Processing Systems(NIPS). Cambridge,M A,USA:MIT Press,1998:682-688.

[4] Belkin M,Niyogi P.Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation,2003,15(6):1373-1396.

[5] Van-der-Maaten L J P,Postma E O,Van-den-Herik H J.Dimensionality reduction:a comparative review[EB/OL].http://ict.ewi.tudelft.nl/～ lvandermaaten/Publications-files/JM LR-Paper.pdf,2009-10.

[6] He X F,Niyogi P.Locality preserving projections[C]//Neural Information Processing Systems(NIPS).Cambridge,M A,USA:M IT Press,2003:153-160.

[7] He X F,Cai D,Yan S C,et al.Neighborhood preserving embedding[C]//IEEE International Conference on Computer Vision(ICCV).Washington,DC,USA:IEEE Computer Society,2005:1208-1213.

[8] Yang J,Zhang D,Yang J Y,et al.Globally maximizing,locally minimizing: Unsupervised discriminant projection with applications to face and palm biometrics[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(4): 650-664.

[9] Qiao L,Chen S,Tan X,Sparsity preserving projections with applications to face recognition[J].Pattern recognition,2010,43(1):331-341.

[10]Yan S C,Xu D,Zhang B Y,et al.Graph embedding and extensions:a general framework for dimensionality reduction[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(1):40-51.

[11]He X F,Yan S C,Hu Y X,et al.Face recognition using Laplacianfaces[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(3):328-340.

[12]Chen H T,Chang H W,Liu T L.Local discriminant embedding and its variants[C]//IEEE Conference on Computer Vision and Pattern Recognition(CVPR).Washington,DC,U SA:IEEE ComputerSociety,2005:846-853.

[13]Wang H,Yan S C,Xu D,et al.Trace ratio vs.ratio trace for dimensionality reduction[C]//IEEE Conference on Computer Vision and Pattern Recognition(CV PR).Washington,DC,U SA:IEEE Computer Society,2007:1-8.

[14]Cai D,He X F,Han JW,et al.Orthogonal Laplacianfaces for face recognition [J].IEEE Transactions on Image Processing,2006,15(11): 3608-3614.

[15]He X,Cai D,Niyogi P.Laplacian score for feature selection[C]//Neural Information Processing Systems(NIPS).Cambridge,M A,U SA:MIT Press,2005:507-514.

[16]Bishop C M.Pattern recognition and machine learning[M].New York:Springer,2006.

[17]Wu M,Scholkopf B.A local learning approach for clustering[C]//Neural Information Processing Systems(NIPS).Cambridge,MA,USA:MIT Press,2006:1529-1536.

[18]Martinez A M,Kak A C.PCA versus LDA[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(2):228-233.

[19]Lee K C,Ho J,Kriegman D J.Acquiring linear subspaces for face recognition under variable lighting[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(5):684-698.