40 t轴重货车轮轨动力特性分析

杨春雷,李 芾,黄运华,张显锋,吴长波

(1 西南交通大学 机械工程学院,四川成都610031;2 南车眉山车辆有限公司 产品开发部,四川眉山620032)

按照《中长期铁路网规划》和铁路技术政策,我国部分铁路将逐步实现客货分线,铁路货运能力得到大幅提升。为做好客货分线后货车技术储备,满足铁路运输发展需要,各铁路货车设计制造企业、科研院所及大专院校,纷纷开展了新型大轴重货车技术研究工作,提出了新一代大轴重货车综合技术要求[1-3]。本文即根据40 t轴重货车的结构特点,利用车辆—轨道耦合动力学理论[4],建立重载货车车辆-轨道空间耦合动力学分析模型,针对不同速度和不同线路激扰下40 t轴重货车的轮轨动力特性进行了仿真计算分析。

1 重载货车车辆-轨道耦合动力学分析模型

结合40 t轴重货车的结构特点,建立的力学分析模型如图1所示。车体考虑纵向、横移、沉浮、侧滚、摇头和点头6个自由度,并在摇枕和车体间考虑心盘回转摩擦阻力矩和弹性常接触旁承摩擦阻力矩;摇枕考虑除点头外其他自由度,侧架考虑除侧滚外其他自由度,在侧架和摇枕间考虑了摩擦楔块所提供的摩擦阻尼特性,在轴箱悬挂处考虑轴向剪切垫提供的一系悬挂纵向、横向和垂向刚度和阻尼;轮对考虑除纵向外所有自由度。而轨道模型采用3层连续离散点支承无限长Euler梁模型,考虑钢轨的垂向、横向和扭转自由度;轨枕视为刚性体,考虑轨枕的垂向、横向以及刚体转动;道床离散为刚性质量块,道床块之间由剪切刚度元件和剪切阻尼元件相连,道床和路基之间用线性弹簧和阻尼元件连接,只考虑道床的垂向振动。重载货车车辆—轨道耦合模型自由度如表1所列。

图1 重载货车车辆-轨道耦合作用模型(端视图)

表1 重载货车车辆-轨道系统模型自由度

2 轮轨动力特性分析

2.1 直线运行仿真分析

为了重点分析40t轴重货车在不同速度等级和不同轨道谱激扰下的轮轨动力响应情况,文中分别对美国5级谱、中国3大干线谱和德国低干扰谱,在40～100 km/h速度等级下进行了仿真计算。轨道结构均考虑为60 kg/m钢轨,Ⅱ型混凝土轨枕,普通碎石道床[4]。计算结果如图2所示。

图2 40 t轴重矿石敞车在不同激扰和速度等级下的轮轨动力响应

由图2各指标来看,德国低干扰谱明显优于美国5级谱和3大干线谱,3大干线谱则处在德国低干扰谱和美国5级谱之间,这与文献[4]关于轨道谱研究的结论是一致的。

从轮轨垂向力响应来看,轮轨垂向力随着速度的增大而增大。在德国低干扰谱激扰下,其值增加较小;在三大干线谱作用下,速度低于60 km/h时,其值变化不明显;当速度超过60 km/h后,则增加较快,在70 km/h时,已超过英国铁路BR和文献[4]所建议的250 kN的限值;在美国5级谱激扰下,速度在40 km/h时,轮轨垂向力就超过了250 kN,随着速度的增加,垂向力几乎线性增加,当速度为100 km/h时,最大轮轨垂向力已达到290.5 kN。

从图2(b)可以发现,轮轨接触应力随着速度的增加而增大,在3大干线谱激扰下,其值在1 230～1 270 MPa;在美国5级谱激扰下,其值在1 260～1 300 MPa;而在德国低干扰谱作用下,基本在1 200～1 220 MPa之间。明显高于25 t轴重车辆在同样运行条件下的轮轨接触应力值(约1 126 MPa)。这说明大轴重货车更容易对钢轨产生疲劳伤损破坏,重载线路必须严格控制轨道不平顺幅值,车辆应以较低速度运行。

图2(c)是轮轴横向力的变化关系。从图中可以看出,轮轴横向力随速度增加有所增大,但幅值较小,最大轮轴横向力不到40 kN,远低于GB5599—85《铁道车辆动力学性能评定和试验鉴定规范》所要求的许用轮轴横向力(约119 kN)。这说明该车横向稳定性较好,不会发生蛇行失稳现象。

图2(d)是钢轨垂向位移的变化关系。从图中可以看出,速度越高,钢轨垂向位移越大,即对轨道的垂向破坏作用也越大。对比3种线路谱,美国5级线路谱对钢轨的垂向破坏作用最大(最大为2.1 mm),中国3大干线谱次之,而德国低干扰谱相对较小(最大为 1.735 mm)。所以,从维护线路,延长轨道使用寿命来看,也需要保持钢轨平直顺滑,降低钢轨不平顺幅值。

2.2 曲线通过运行仿真分析

为了分析40 t轴重货车的曲线通过性能,本文对该车进行了曲线通过仿真分析。由于在直线仿真计算时已考虑了不同轨道谱对轮轨动力特性的影响,这里就不再进行不同轨道谱间的对比分析,而只是对比有无线路轨道谱的轮轨动力响应差别。曲线工况如表2。轨道结构为60 kg/m钢轨,Ⅱ型混凝土轨枕,普通碎石道床。计算结果如图3、图4所示。

表2 曲线仿真计算工况

图3(a)是轮轨横向力曲线通过时的动态变化情况。从图中可以看出,内外侧轮轨横向力方向始终相反,内侧向内,外侧向外。速度为40 km/h时,轮轨横向力外侧值较内侧值小;在速度为55 km/h时,内外侧值基本一致;当速度为65 km/h时,外侧值则大于内侧值。这是由于对于曲线半径为300 m,超高为120 mm的曲线线路,向心力与离心力平衡的速度约是55 km/h[6]。所以,在速度为55 km/h时,内外轮轨横向力大小基本一致,而速度为40 km/h和65 km/h时,则分别产生过超高和欠超高现象,从而造成内外轮轨横向力差异。

从图3(b)看,速度为55 km/h时,左右车轮均载,轮轨垂向力都在196 kN(静轮载)左右;在40 km/h时,外侧减载,内侧增载;在 65 km/h时,外侧增载,内侧减载。从图3(d)来看,钢轨的横移与轮轨横向力变化一致,即在40 km/h时,内侧值较大;在65 km/h时,外侧值较大;而在55 km/h时,因内外轮轨横向力一致,内外钢轨横向变形也比较平均。

图3 曲线通过时的轮轨动力响应(无激扰)

图4是车辆在3大干线谱激扰下曲线通过时的轮轨动态变化情况,为清晰反映轨道不平顺对轮轨产生的影响,图中对无线路激扰和添加激扰两种情况进行了对比分析。从轮轨力的动态变化来看,轨道不平顺并不影响车辆曲线通过的基本规律,只影响轮轨响应输出的幅值。速度为40 km/h时,最大轮轨横向力从57.64 kN增大到71.72 kN(内侧),最大轮轨垂向力从224.2 kN增大到263.6 kN(内侧);在55 km/h,最大轮轨横向力从50.49 kN增大到77.72 kN,最大轮轨垂向力从201.2 kN增大到251.8 kN;而在65 km/h,最大轮轨横向力从58.97 kN增大到79.57 kN,最大轮轨垂向力从215.3 kN增大到268.4 kN(外侧)。从图示和以上数据可以看出,重载车辆在曲线通过时,速度过低和过高都会使某一侧车轮增载或减载,在有不平顺激扰时就更为突出。所以,为降低轮轨垂向相互作用,根据曲线超高和曲线半径选定适当的运行速度是必要的,尽可能使向心力和离心力平衡。

3 结论及建议

本文根据40 t轴重重载货车的主要技术性能和结构特点,利用车辆-轨道耦合动力学原理,建立了重载货车车辆-轨道耦合模型,对车辆轮轨动力特性进行了仿真分析,可以得出如下结论及建议:

(1)大轴重货车轮轨相互作用特别是垂向相互作用明显加大,不同的轨道谱和不同的车辆运行速度将产生不同的轮轨动力响应。速度越高,轮轨动力作用越大,线路状况越恶劣,轮轨动力作用也越大。根据我国现有重载线路状况,按照英国铁路BR和文献[4]所建议的轮轨垂向力为250 kN的限值,则40 t轴重重载货车的运行速度以不超过70 km/h为宜。

(2)仿真计算表明,车辆在通过曲线时,速度过低和速度过高都将引起车辆某一侧增载,应根据各曲线段情况采用适当的速度,尽可能使车辆离心力与向心力平衡。

(3)我国尚缺乏重载铁路相关评价标准,应开展重载铁路基础性研究工作,尽快制定出重载铁路轮轨相互作用评价指标体系,如轮轨垂向力、轮轨接触应力、轮轨磨耗功、钢轨振动加速度等评价指标限度。

[1] 铁道部运输局.关于新型大轴重铁路货车技术研究有关工作的通知[S].运装货车[2009]318号,2009.

[2] 南车眉山车辆有限公司.40 t轴重矿石敞车设计方案说明[R].2009.

[3] 南车眉山车辆有限公司.40 t轴重转向架设计方案说明[R].2009.

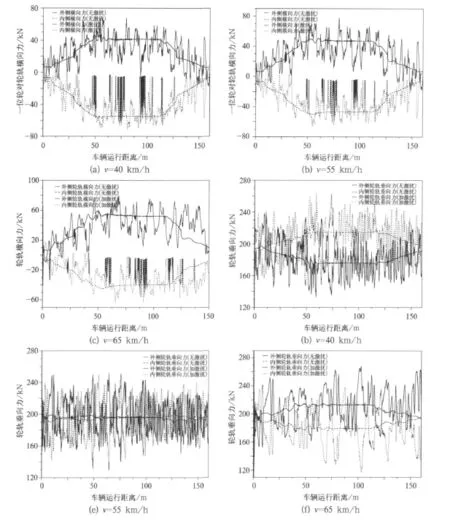
图4 曲线通过时的轮轨动力响应(3大干线谱激扰)

[4] 翟婉明 著.车辆-轨道耦合动力学(第2版)[M].北京:中国铁道出版社,2001.

[5] 西南交通大学.40 t轴重转向架动力学性能计算报告[R].2008.

[6] 严隽耄 主编.车辆工程(第3版)[M].北京:中国铁道出版社,2008.