“5.12”汶川地震中高大加筋土挡墙破坏机理研究

陈 强，杨长卫，张建经，周新文

(1.成都理工大学，成都 610059;2.四川省交通厅 公路规划勘察设计研究院，成都 610041;3.西南交通大学 土木工程学院，成都 610031;4.南宁铁路局，南宁 530003)

加筋土挡墙的柔性特点使其具有良好的抗震性能。在5.12汶川地震中，共有两处加筋土挡墙发生破坏，一处是由于地震动造成的破坏，另一处是由于断层移动造成的破坏，因此，有必要对加筋土挡墙的抗震破坏机理做进一步的研究。本文以汶川地震中地震动造成的破坏挡墙为分析对象，利用有限元方法，建立了该加筋土挡土墙的分析模型，并开展了详细分析。通过比较该加筋土挡墙的震害与分析结果，揭示了加筋土挡墙的抗震破坏机理。

1 工程概况

所研究的加筋土挡墙位于国道213都江堰至映秀段。该线路以高路堤通过山间谷地，工况控制点在曾家沟大桥附近，左侧为岷江，右侧靠山，抗震设计设防烈度为7度。地基表层为中度风化的白云岩，厚2～3 m，下部为微风化的白云岩。该加筋土挡土墙为双级复合加筋带挡墙。挡墙分两级施工，上墙高10 m，下墙高10 m。挡土墙采用C25的混凝土条形基础，均做成台阶式。上墙的条形基础坐落在下墙的墙后填土上，两级墙的墙面间距是1.2 m。压顶均采用 C25的混凝土，台阶处压顶为厚0.3 m，宽0.7 m的条形混凝土梁，路基顶部压顶为调平层，宽0.7 m，高度由路面而定。挡墙面板采用C20的钢筋混凝土矩形预制板，面板长0.60 m，宽0.25 m，厚0.20 m，每一块面板中部预埋一个拉筋连接环。拉筋采用CAT300200C钢塑复合加筋带，极限抗拉强度为12 kN，破断伸长率<1%。拉筋分层铺设于填土表面，层间距0.5 m。自路基表面向下0～5 m内，拉筋长11 m，水平间距0.25 m;5～10 m内，拉筋长10 m，水平间距0.25 m;10～15 m内，拉筋长9 m，水平间距0.25 m;15～20 m内，拉筋长8 m，水平间距0.16 m。

2 计算模型

本文运用有限元软件PLAXIS对加筋土挡土墙进行数值模拟，模型的几何尺寸和截面的几何特性依据施工图确定。PLAXIS中存在实体和构件两种单元建模方式。为了尽可能真实地模拟填土、地基、面板的力学性能，本文对其采用实体建模。由于拉筋带只承受拉力，不能抗弯、抗压，故采用土工格栅单元模拟。加筋土挡墙的面板与面板之间主要靠摩擦连接，为了真实反映面板之间的相互作用，在面板间的接触处设置了接触单元，以模拟其力学性能。拉筋带直接穿在面板上的拉环中，本文利用塑性铰来模拟，以反映拉筋带与面板之间的相互作用。混凝土压顶、面板、加筋带、条形基础、地基与填土之间通过设置接触单元来模拟它们之间的相互作用。填土为碎石土，采用摩尔—库伦本构模型描述其力学行为。条形基础、面板、岩石地基采用线弹性本构模型。接触单元采用Goodman本构模型。考虑到拉筋带会产生塑性变形，故采用弹塑性本构模型。为了尽可能减小边界的影响，在模型的底部和左右两侧设置吸收边界。图1为实际结构的示意图，图2显示了面板与面板连接和面板与筋条连接的细部构造。

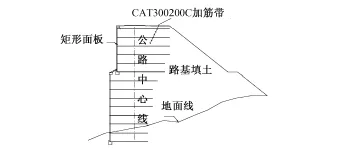
图1 结构示意

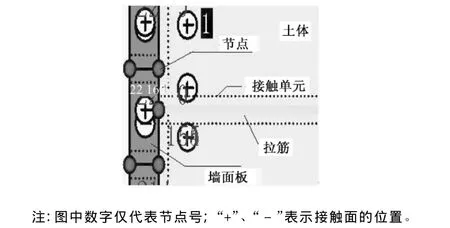
图2 节点详图

3 动力有限元分析原理

根据虚功原理或达朗贝尔原理建立平衡方程。在地震荷载作用下，有限元体系在t+Δt时刻的运动平衡方程为

式中，M是体系的总质量矩阵;u是体系的节点位移矢量;˙u是体系的节点速度矢量;¨u是体系的节点加速度矢量;C是体系的总阻尼矩阵;K是体系的总刚度矩阵;F是体系的节点地震荷载矢量。

目前，动力运动平衡方程的求解方法有两种。一种是反应谱法。这种方法通过先求解无阻尼自由振动的方程，获得挡墙体系的自振频率与振型，之后，通过模态分析与反应谱法，求得挡墙的动力响应，确定动位移、动应力的分布。另一种是时程分析法，即直接采用数值积分的方法求解方程式(1)，得到挡墙动力响应时程曲线，是一种完全动力法。

Rayleigh阻尼即 C=αM+βK。式中，C为阻尼矩阵，α、β为 Rayleigh阻尼系数，M 为质量矩阵，K为刚度矩阵。α、β可以根据阵型分解法由选定的两个阵型的阻尼比和相应的自振频率表示如下。

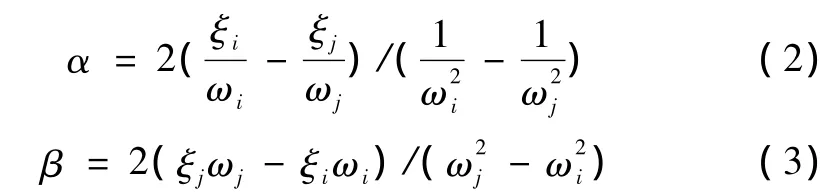
式中，ξi、ξj和 ωi、ωj分别为第 i、j阵型的阻尼比和相应的自振频率。

竖向地震荷载的主要作用是使填土与地基土变得更加密实。它对加筋土挡墙面板的水平位移、加筋内力以及墙体加速度特性影响不大［1］，因此，本文忽略了竖向地震作用，只施加了水平地震波。考虑到该加筋土挡墙和卧龙台站距汶川地震活动断层的距离相近，为了真实反映汶川地震中该加筋土挡墙的抗震性能，本文在分析中选择输入的地震波是在汶川地震中卧龙台站实测的地震波。卧龙波的持时是180 s，峰值加速度为975 cm/s2，加速度时程曲线如图3所示。地震波由计算模型的底边界输入。该模型的左右为固定边界，边界反射的振动可能会影响加筋土挡土墙的动力响应。本文通过在模型两侧增设吸收边界来解决。

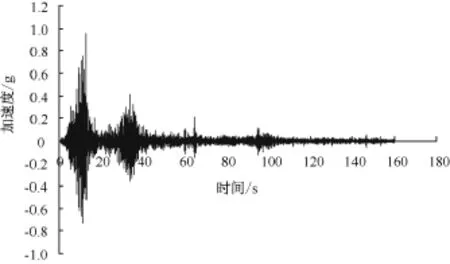
图3 卧龙波加速度时程曲线

为了研究在不同地震烈度情况下加筋土挡墙的动力响应，本文通过调节卧龙波的峰值加速度，得到峰值加速度为0.200 g、0.400 g、0.957 g的地震波，并在模型底部分别施加了以上三种地震波。

填土、基岩、面板的力学特性参数见表1，拉筋的力学特性参数见表2。

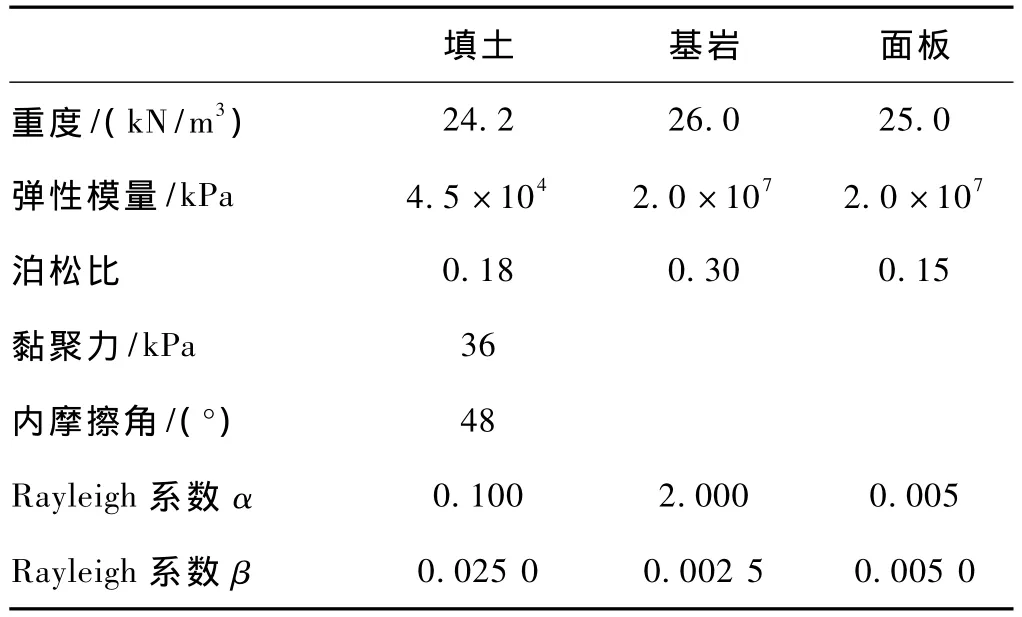
表1 填土、基岩、面板的材料力学特性参数

表2 拉筋力学特性参数

4 计算结果

本节出现的“0.200 g、0.400 g、0.957 g”分别表示所施加地震波的峰值加速度。“有限元上”、“有限元下”表示通过动力有限元计算得到的上墙、下墙的动力响应。“库伦上”、“库伦下”表示依据规范得到的上墙、下墙的动力响应。“静力上、0.200 g上、0.400 g上、0.957 g上”分别表示在静力、0.200 g、0.400 g、0.957 g地震波作用下利用有限元方法计算得到的上墙的动力响应。“静力下、0.200 g下、0.400 g下、0.957 g 下”分别表示在静力、0.200 g、0.400 g、0.957 g地震波作用下通过有限元计算得到的下墙的动力响应。

4.1 墙体位移

为了研究在不同峰值加速度地震波作用下，加筋土挡墙水平位移沿墙高的分布情况，本文自上而下共布置了 10 个位移测点，即 A1、B1、C1、D1、E1、F1、G1、H1、I1、J1。其中，A1、B1、C1、D1、E1五点位于上墙墙后填土内，各点间距均为 2.5 m，约 5块板高。F1、G1、H1、I1、J1五点位于下墙墙后填土内，其中，F1、G1两点的间距为1 m，其余点间的距离均为2.5 m。由图4、图5可得以下结论:

图4 墙体水平位移沿墙高分布曲线

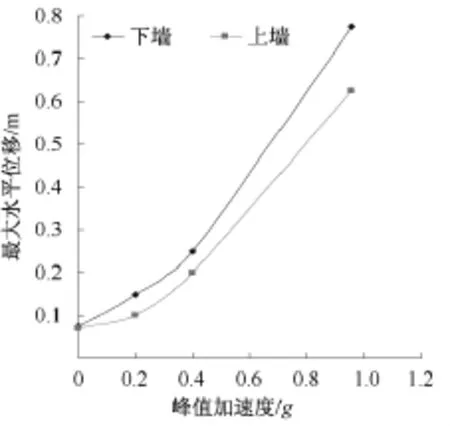
图5 上、下墙最大水平位移随峰值加速度变化曲线

1)上墙墙顶水平位移随地震烈度的增加而增加。图4显示，静力作用下，上墙墙顶水平位移为0.072 50 m;0.200 g地震波作用下，上墙墙顶水平位移为0.010 23 m;0.400 g地震波作用下，上墙墙顶水平位移为0.204 50 m;0.957 g地震波作用下，上墙墙顶水平位移为0.654 80 m。

2)上墙的墙体位移模式基本上不随地震烈度的增加而变化，墙体始终是绕基础的转动和自身的平动相结合，但随地震烈度的增加，上墙绕基础的转角和自身的平动量逐渐增大。

3)随地震烈度的增加，下墙的最大水平位移点逐渐升高。图4显示，在0.957 g、0.400 g地震波作用下，下墙的最大水平位移出现在距墙趾9 m附近;在0.200 g和静力作用下，下墙的最大水平位移出现在距墙趾6 m附近。

4)随地震烈度的增加，上、下墙的最大水平位移逐渐增加，且呈非线形增长。图5显示，当峰值加速度由0.200 g变为0.400 g时，上、下墙的最大水平位移约增加了2倍;当峰值加速度由0.400 g变为0.957 g时，上、下墙的最大水平位移约增加了3倍。

5)由各点的位移值与面板宽度间的关系可推知，在静力、0.200 g、0.400 g地震波作用下，挡墙没有发生破坏;在0.957 g地震波作用下，下墙台阶处发生过大水平位移，造成墙体局部破坏。

4.2 水平加速度

本节中各点的加速度放大系数C=各点实测地震波的峰值加速度/卧龙波的峰值加速度。

为了研究水平加速度沿墙高的放大系数及在高烈度情况下水平加速度放大性与测点距面板远近之间的关系，本文分别在挡墙面板后0.2 m处和路基中线自上而下均匀布置了10个加速度测点。由图6、图7可得以下结论:

图6 不同烈度地震作用下水平加速度放大系数

1)随地震烈度的增加，水平加速度沿墙高的放大比逐渐降低。由图6可知，在0.957 g地震波作用下，水平加速度沿墙高的放大系数在0.85～1.00之间;在0.400 g地震波作用下，水平加速度沿墙高的放大系数在1～2之间;在0.200 g地震波作用下，水平加速度沿墙高的放大系数在1～3之间。以上现象主要是:由于随地震烈度的增加，加筋土挡墙墙后填土中塑性区增加，增加了耗能，从而引起加速度放大比降低。

图7 0.957 g地震波作用下水平加速度放大系数

2)在高烈度情况，距挡墙面板距离越近，水平加速度放大系数越小。图7显示，在0.2 m处的水平加速度放大系数小于路基中央的水平加速度放大系数，但均<1。本文认为其主要是由于地震烈度过大，土体内的塑性区过大，造成耗能过大，引起加速度衰减。

4.3 墙背土压力

为了研究在不同峰值加速度地震波作用下，加筋土挡墙墙背土压力沿墙高的分布情况，本文在墙体面板内自上而下均匀布置了10个土压力测点。

目前，在国内外抗震设计规范中，挡土墙的稳定性验算均采用拟静力法。为了研究在不同地震烈度下，有限元和规范两种关于加筋土挡墙墙背土压力计算方法之间的差异，本文通过对加筋土挡墙施加峰值加速度为0.200 g、0.400 g、0.957 g的地震波，并将有限元计算结果与规范计算结果进行了比较。结合图8、图9、图10、图11，可以得到以下结论:

图8 静力作用下墙背土压力分布

1)当地震动峰值加速度不大于0.400 g时，上墙墙背土压力的有限元计算结果与规范计算结果基本一致。

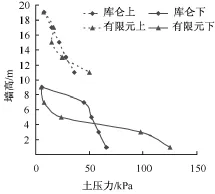
图9 0.200 g地震波作用下墙背土压力分布

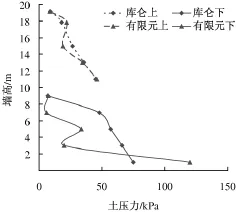
图10 0.400 g地震波作用下墙背土压力布

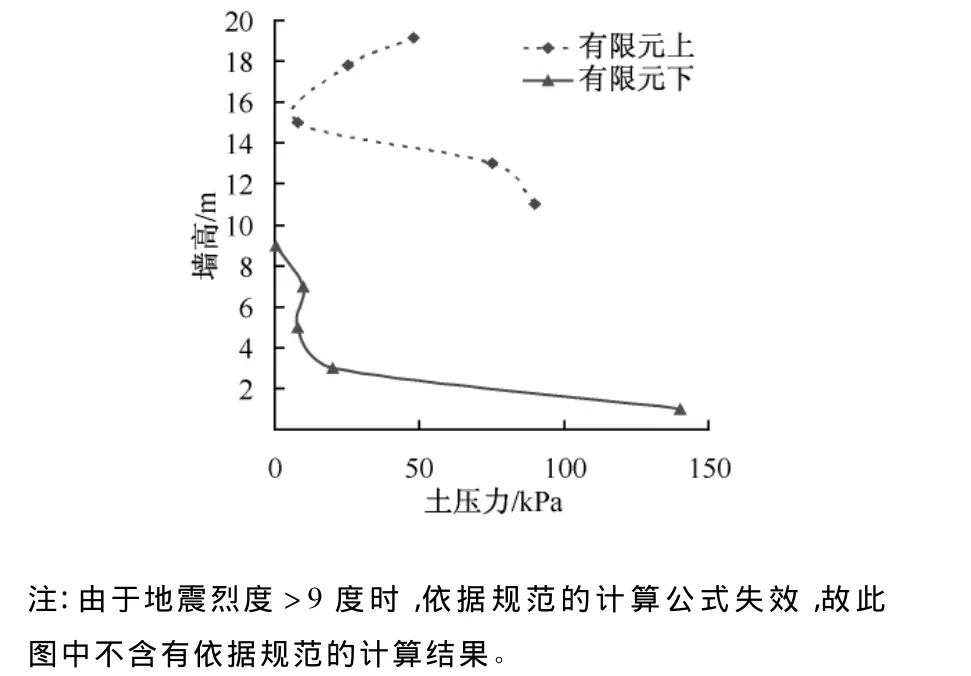
图11 0.957 g地震波作用下墙背土压力分布

2)随地震动峰值加速度的增加，下墙墙背土压力的有限元计算结果与规范计算结果之间的差异逐渐增加，规范计算结果偏大。

4.4 破坏形态分析

图12圆圈内的位移分布显示了挡墙面板处的水平位移最大值为785.74 mm，且在台阶下方出现了位移集中。图13为加筋土挡墙的实际破坏图。通过图12与图13的比较可知，有限元计算结果与实际破坏情况基本吻合。台阶处出现破坏主要由于以下几点。第一，由图13知，该处出现位移集中，并存在应力集中现象，主要与台阶尺寸太小有关。第二，面板与加筋带的连接处是沿筋带长度范围内最薄弱的区域。第三，上墙基础沉降量较大，挤压下墙顶部筋条，使面板向后移，而墙后填土为弹性模量较大的碎石土，阻碍面板向后移动，造成筋条受力过大，从而引起挡墙破坏。下墙顶部破坏区以下拉筋的抗拉拔力能有效地抵抗土压力，所以，挡墙并未发生整体垮塌。

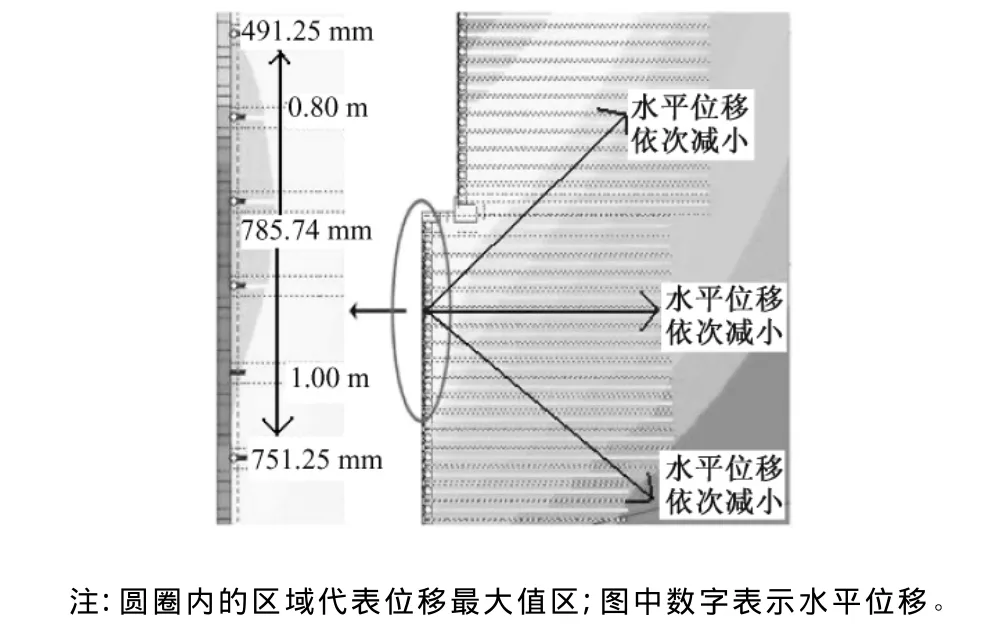
图12 水平位移大样图

图13 实际破坏情况

5 结论

通过以上分析，得到以下具体结论及建议:

1)在地震动峰值加速度 <0.400 g的情况下，两级加筋土挡墙的水平加速度沿墙高具有放大性，并且随地震烈度的增加，水平加速度的放大性逐渐减小;在地震动峰值加速度为0.957 g时，水平加速度沿墙高逐渐减小。

2)在高烈度地震作用下，水平加速度沿墙高逐渐降低，在靠近挡墙面板处，水平加速度衰减得最厉害。

3)在施工过程中，要保证合理的台阶宽度，防止台阶处出现应力和位移集中现象;适当加密台阶处的拉筋，保证其具有足够的抗拉拔能力;尽量地压密面板处的土体，保证该处拉筋具有足够的摩阻力;适当增加拉筋上覆盖层的厚度，特别是下墙顶部拉筋带的上覆盖层厚度，以防止上墙基础因变形过大而直接压在拉筋上。

4)随地震烈度的增加，两级加筋土挡墙中，上墙墙顶的水平位移逐渐增加，但上墙的运动形式不发生变化，即始终为绕上墙条形基础的转动与平动相结合。这种现象主要是由于上墙的地基是下墙的墙后填土，下墙的水平位移则是随地震烈度的增加而逐渐变化。在高烈度地震作用下，最大水平位移出现在台阶处;在低烈度地震作用下，最大水平位移出现在下墙中部。这种现象主要与台阶的宽度有关。在目前各国的抗震规范中，还没有明确提出一套关于高烈度区两级加筋土挡墙的设计标准，因此，对于高烈度区两级加筋土挡墙的抗震设计，应作单独深入的研究。

5)在地震动峰值加速度 <0.400 g时，上墙墙背土压力的规范计算结果与有限元计算结果基本吻合，下墙墙背土压力的规范计算结果大于有限元计算结果，两者之间的误差随地震烈度的增加而增加，因此，如果依据规范进行设计，则偏于保守。由4.1节墙体位移可知，该加筋土挡墙在0.400 g地震波作用下没有发生破坏，但是，该挡墙为7级设防标准。这种现象主要是由于依据规范计算下墙时，将上墙作为均布荷载施加在下墙顶部，忽略了地震作用下上墙惯性力对下墙的影响，而有限元则考虑了地震作用下上、下墙之间的相互作用。因此，在低烈度区，由于地震动所引起的惯性力较小，忽略上墙惯性力对下墙的影响，所产生的误差较小，所以，采用规范土压力计算方法是可行的。但是，在高烈度区，由于地震动所引起的惯性力较大，忽略上墙惯性力对下墙的影响，可能会产生较大误差，因此，对于高烈度区两级加筋土的挡墙的地震土压力计算方法仍需进一步研究。

［1］刘华北.水平与竖向地震作用下土工格栅加筋土挡墙动力分析［J］.岩土工程学报，2006(28):594-599.

［2］周世良，格栅加筋土挡墙结构特性及破坏机理研究［D］.重庆:重庆大学，2005.

［3］陈忠达.公路挡土墙设计［M］.北京:人民交通出版社，1999.

［4］王立强，王元站，迟丽华.挡土墙地震土压力及其分布［J］.中国港湾建设，2007，26(5):1-5.

［5］陈华，赵有明，张发春.土工格栅加筋土挡墙施工工况有限元分析［J］.重庆交通大学学报，2009，28(6):1088-1091.

［6］陈华.塑料土工格栅加筋土挡墙动力有限元分析［D］.昆明:昆明理工大学，1999.

［7］李海光.新型支挡结构设计与工程实例［M］.北京:人民交通出版社，2004.

［8］马存明，周亦唐，廖海黎，等.塑料土工格栅加筋土抗拉拔特性试验研究［J］.中国铁道科学，2004，25(3):36-39.