GPS动态测量中系统误差的分离方法

汤 云,金元刚,付 平

(1.解放军92941部队,辽宁葫芦岛125001;2.中海油能源发展有限公司,天津300450)

0 引 言

在动态测量数据处理中,系统误差是很棘手的问题,研究系统误差的有效处理方法正受到越来越多的关注。系统误差的特性非常复杂,既具有延续性,又有偶然性,因而很难用统一的、确定性的模型来准确描述它。就GPS动态测量来说,信号受到多种误差源的误差干扰,有的误差(例如电离层折射影响)可以利用双频接收机的方式得到较好补偿,而多路径影响却很难找到有效的改正模型。系统误差虽经部分模型改正,或差分改正,仍有部分残余留在观测量中,或多或少影响到定位结果的精度[1]。

在很多GPS定位技术的文献资料上,定位误差都按如下方法进行估计[2]

式中:ei是第i次采样的误差;n为样本容量;¯x为系统误差;σ为标准差。

上述误差估计方法的误差模型是用随机变量来描述的。对于GPS静态定位或静态测量时是正确的,但将这种方法用于GPS动态定位或动态测量中一般是不正确的,因为只有当系统误差是常量时,该方法才可适用。而实际上GPS动态测量的系统误差一般并不是常量,其误差曲线并不水平。对于GPS动态测量系统的误差估计,应力求提高误差估计结果的精度或可信度。为了科学客观地评定一个GPS动态测量系统的性能,有必要研究适合GPS动态测量的数据处理方法。

1 GPS动态测量的误差特性

GPS动态测量的误差是随机过程或经采样以后形成的随机序列,当用户台处于动态时,这是很显然的。在GPS动态测量系统的鉴定试验中,可以采用静态目标试验动态性能,这种方法尽管是采用静止目标,但本质上不同于静态测量。因为噪声引起的误差、传播介质产生的误差(包括电离层、对流层折射和多径效应引起的误差)、卫星钟差、卫星星历误差等经差分后的残余误差都是随机过程,采用单历元解算,这种特性被保留下来并离散化为随机时间序列。

GPS测量的误差中,传播介质产生的误差、卫星钟差、卫星星历误差等存在随时间慢变的成分;不同历元可能有不同导航卫星的信息参与运算,其DOP值一般情况下也是不同的,由此产生的误差也是随时间变化的;在载波相位差分定位中,周跳引起的误差在不同历元也是变化的。这些随时间慢变的误差成分形成了系统误差,它们并不表现为常值,而是时间的随机函数。除上述慢变成分外,它们的快变部分以及噪声引起的误差则成为噪声状态的随机误差部分。

GPS动态测量系统的误差是由热噪声、量化噪声、电离层和对流层折射产生的误差、卫星钟差、卫星星历误差、基准站误差、模糊度解算误差等许多误差分量综合的结果。在接收机和卫星系统正常工作的情况下,各种误差对总误差的影响都不显著。根据中心极限定理,系统测量误差的概率分布为正态分布。

综合以上分析,GPS动态测量系统的动态测量误差是非平稳的正态随机序列。误差的这一特性是研究数据处理方法的出发点。

2 处理方法的理论基础

2.1 非平稳随机过程误差处理方法

动态测量误差是非平稳的正态随机过程或经采样得到的随机序列,用x(t)表示。其中有变化缓慢的误差成分y(t)和快变的误差成分η(t),即

式中:慢变误差y(t)称为系统误差,而把零均值的η(t)称作随机误差。

根据随机过程的理论,估计动态测量误差 x(t)的均值和方差需得到 x(t)在ti时刻的抽样值x1(ti),x2(ti),…,xn(ti),它们是来自x(ti)的样本点。其中xj(t)是指来自x(t)的第j个样本记录,对应于系统在相同状态下(以保证它们来自同一过程x(t))所做的第j次试验(第j航次、架次)。用随机变量样本值的统计方法(即式(1)和式(2))得到ti时刻的估计。对记录的每一时刻都做如此处理,就可得到均值函数和方差函数[3]。

但是上述处理方法对GPS动态测量误差估计存在很大困难。需要做许多次试验才能保证误差估计的精度。这多次试验要保持系统状态相同可以说是无法实现的。比如,不同次数的试验要求跟踪相同的卫星,要求DOP值相等,这些都是不可能的。因此动态误差的估计需要另想办法。

2.2 各态历经随机过程误差处理方法

按照随机过程理论,如果过程具有各态历经性,则上述估计等价于对一个记录的相应时间均值的估计,即可通过对一个记录时间均值的计算得到x(t)的均值和方差的估计[4]。

经过论证有如下结论:对于只求正态随机过程的一、二阶矩,如果过程是平稳的,则具有各态历经。但是如前所述x(t)一般并不平稳。

对于式(3)中的系统误差y(t),并不同于杂乱无章的噪声,它的出现具有一定规律性。只要试验时间足够长,即可用一个现实(一次试验)数据得到。能否用时间均值作为动态误差的估计,关键是看噪声η(t)是否具有各态历经。将x(t)中的系统误差y(t)分离以后,所剩η(t)如果平稳,理论上就可用一个现实的数据完成误差统计。

3 系统误差分离

系统误差是具有规律性的慢变误差,可以用一个解析函数逼近。由函数逼近理论,如果函数 f(t)在区间[a,b]上连续,则在该区间上总可用一个代数多项式P(t)去一致逼近。用n阶多项式a0P0(t)+a1P1(t)+…+anPn(t)作为系统误差y(t)的模型,由此得

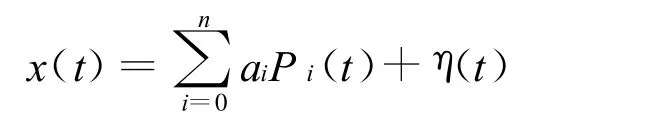
其离散序列为

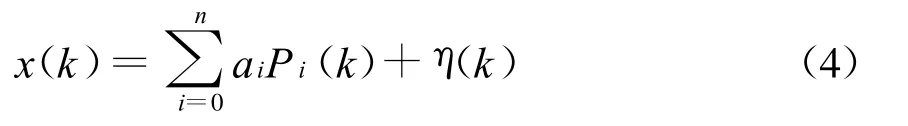
式中:k=1,2,…,N。N为序列长度。令

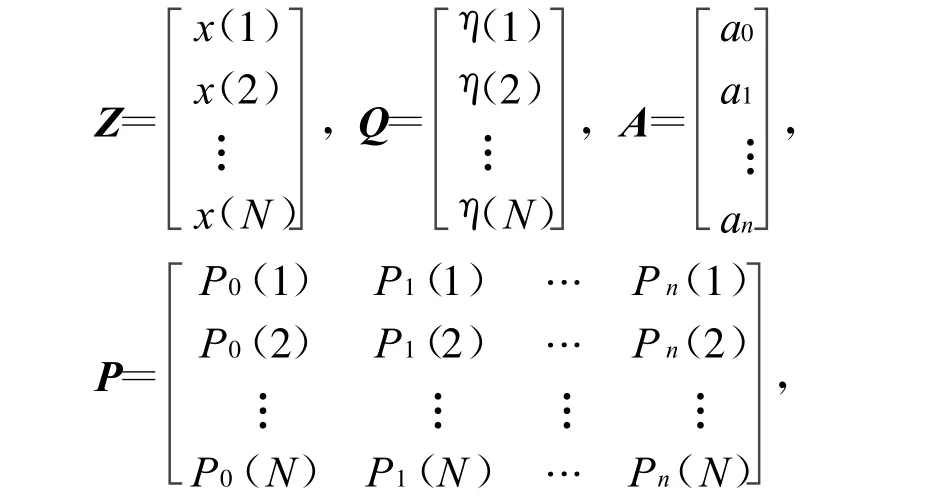
参数A的最优估计为

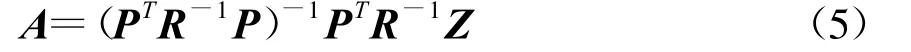
式中:R是Q的方差阵,或者是η(t)的相关函数阵。

假如η(t)二阶平稳且不相关,则可令R-1=I,而实际上η(t)是相关的,并且有时是强相关,尤其在定位处理中采用了卡尔曼滤波后更是如此。为了避免计算R的困难,常用的方法是独立抽样。独立抽样的问题存在相关时间计算是否较为准确,而主要问题是独立抽样引起y(t)的失真。通过频域研究发现独立抽样引起y(t)的失真几乎是不可避免的,这种方法不能得到系统误差的最优估计。

求A的最优估计可考虑如下算法

①令R=I,得到初始估计A0;

②用A0分离系统误差,其残差作为η(k),求方差阵R0。由于A0不是最优估计,R0只是R的初始估计;

③令R=R0,用式(5)估计A得到A1,A1是比A0更好的估计;

④用A1分离系统误差后再次估计R得到R1,R1是比R0更好的估计;

⑤再令R=R1重新估计A,依此循环直到满足计算精度。

这种方法实际上会产生很大的计算误差。GPS动态测量系统采样率一般不低于20 Hz,为了充分考核动态测量精度,一次试验要连续记录30 min以上,误差序列将有几万组以上的采样值。x(t)的方差阵将达几万阶以上,很难保证其正定性。即使能保证正定,这样高阶矩阵的求逆要经过许多步的计算,使计算误差大量累积。

通过研究和实际计算形成了求解系统误差参数的如下方法。

零均值平稳随机序列可用ARMA模型描述,而ARMA可用足够高阶的AR模型模拟,因此,零均值平稳随机序列可用AR模型建模

式中:ε(k)为白噪声;φ(B)为算子多项式

将式(6)代入误差模型式(4),有

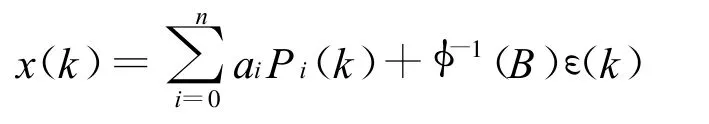
即

令

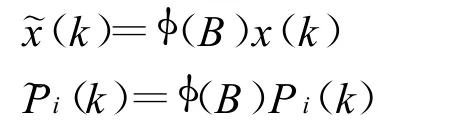
式(7)为

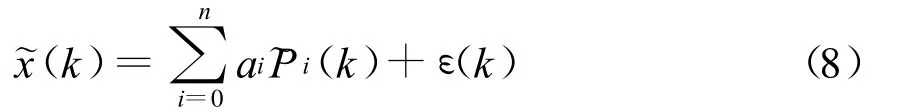
如果得到N+q个样本值,有

式中:

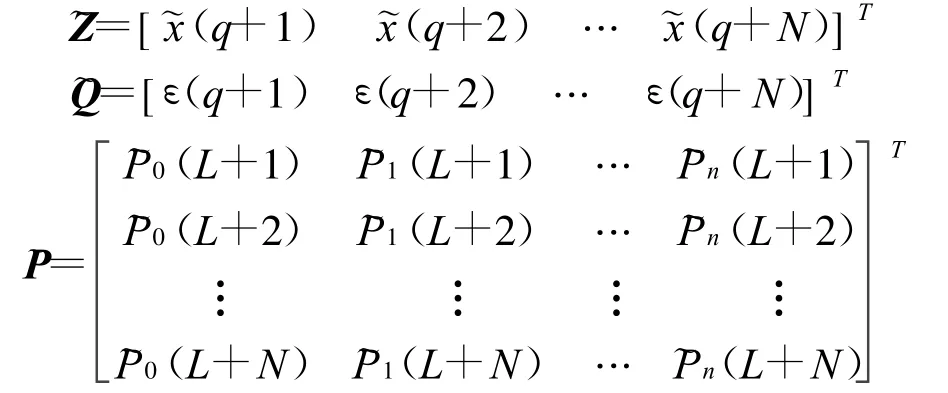
由于ε(k)是零均值白噪声,因此ai的最优估计为

可以进一步推导出AR模型参数的估计

式中:Φ=[φ1 φ2 … φL]T,R(L)是L维随机变量η(k)的方差阵,而 Σ(L)是L维随机变量η(k)的协方差组成的列向量。

Φ还可用最小二乘估计得到

式中:

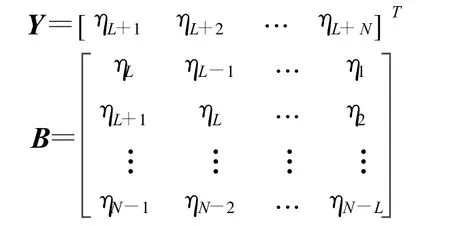
式(11)、式(12)中的R-1(L)和(BTB)-1都只是L阶矩阵求逆,而L不会超过10,显然比几万阶矩阵求逆误差小得多。

计算方法与前述逐次求R矩阵的方法相同。首先令φ(B)=1,得到初始估计A0,进而得到初始估计 Φ0。利用 Φ0重新计算得到A1和 Φ1,直至达到计算精度。

4 实测GPS数据误差分析

为了验证算法的有效性,采用2009年3月20日某无人机飞行记录的GPS测量数据进行多项式拟合及误差分离。无人机飞行了大约1 h,机载GPS的数据更新率是20 Hz,为了作图清晰直观,采用提取1 Hz的实测数据进行处理,数据长度为1000 s。图1～图6是应用前面所述的方法对实测数据的高度和速度进行多项式拟合并进行误差分离的结果。

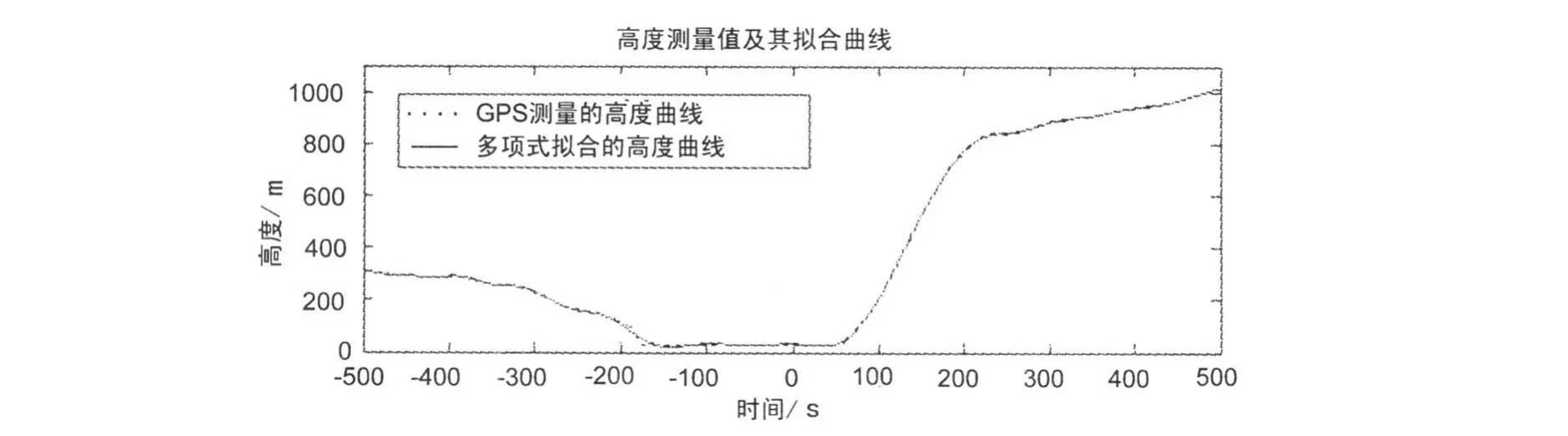
图1 高度测量值及其拟合曲线

图3 高度误差自相关函数

图1、2、3表示的是GPS高度数据分析结果。从图1可以看出,多项式能较好拟合无人机飞行高度曲线;图2、3显示高度误差具有明显的周期性和随机性,其自相关函数缓慢衰减且周期振荡。图4、5、6则表示对与高度记录相同时段所对应的飞行速度曲线分析结果。从分离出的速度误差来看,它与高度误差一样,具有周期性和随机性,其自相关函数同样表现出振荡衰减性质。图2、图5中的出现数据跳变,是因为在此期间无人机处于俯冲阶段,姿态变化较大,引起短暂卫星失锁,使整周模糊度发生跳变所致。对该时段的其他的GPS数据采用上述处理方法,可以得到类似的结论。

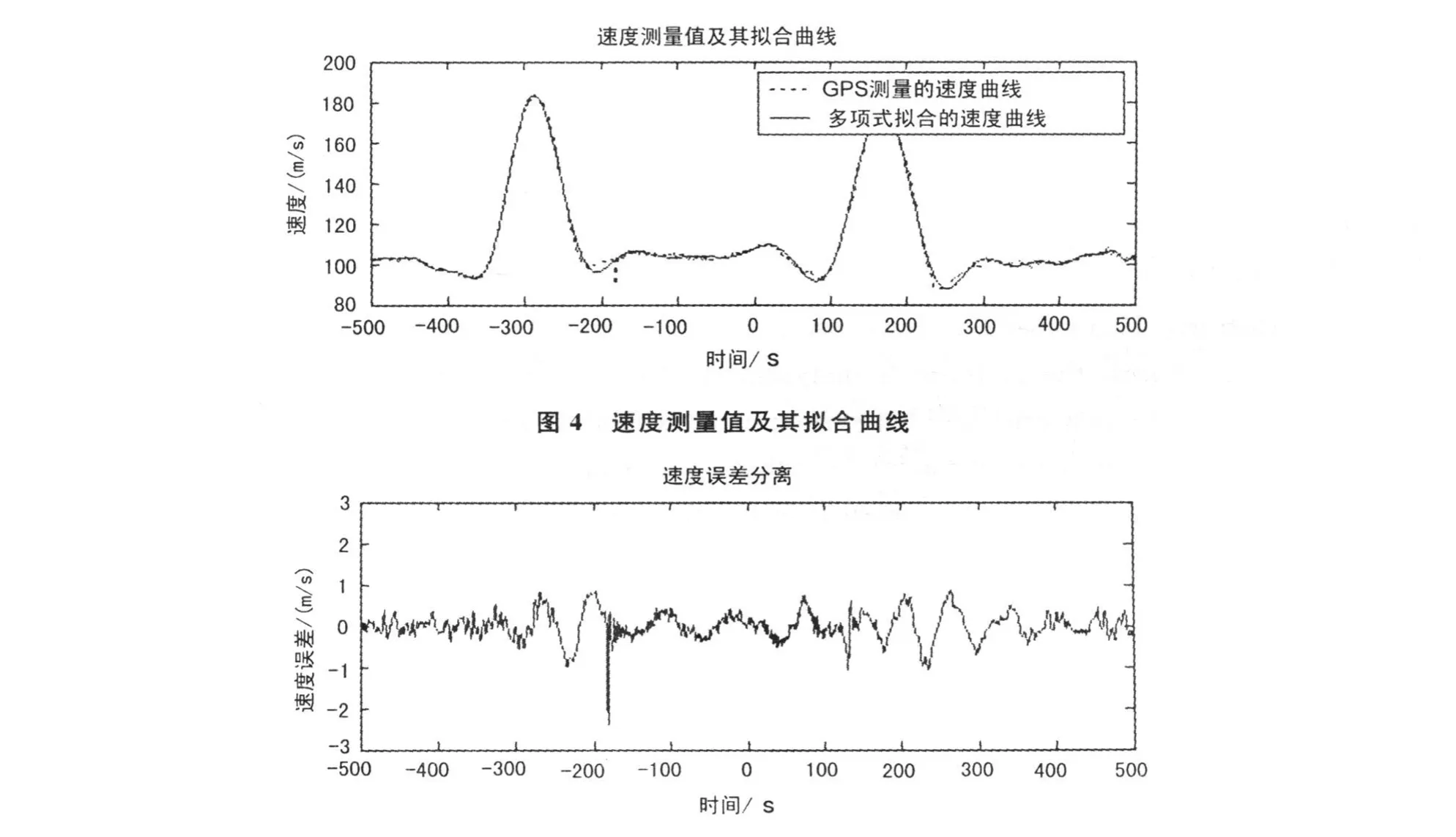
图5 速度误差分离曲线

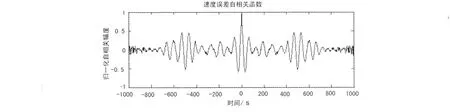
图6 速度误差自相关函数

5 结 论

经过理论分析及实例验证,为GPS动态测量误差的统计分析确立了完整的分析处理方法。除上述误差特性、理论基础、系统误差分离以外,还包括数据的预处理(数据分析、野点判别及修复等)、多项式和AR模型阶数的判别、非线性模型、平稳性检验、随机误差估计的性质及无偏修正、AR模型建模的递推算法、非线性建模方法、利用BTB矩阵性质构造多项式(非正交)参数估计的递推算法等。限于篇幅,这些问题将在后续的研究中再补充讨论。

[1] 欧吉坤,王振杰.GPS精密测量中系统误差的分离方法[J].数据采集与处理,2003,12(4):365-368

[2] 李洪涛,许国昌,薛鸿印,等.GPS应用程序设计[M].北京:科学出版社,1999:256-262

[3] 费业泰.误差理论与数据处理.第5版[M].北京:机械工业出版社,2005:162-174.

[4] 梁晋文,陈林才,何 贡,等.误差理论与数据处理.第2版[M].北京:中国计量出版社,2001:136-162.