GPS高程拟合代替水准测量的可行性①

刘兴春,仲健民,高冰冰

(65015部队,辽宁 大连116031)

0 引 言

GPS高程拟合其实就是要拟合一个符合该区域的似大地水准面模型。GPS所测得的高程是测站相对于世界坐标系椭球面的大地高,而所采用高程系统是正常高系统,存在一个高程异常值,这个值并不是一个常数,而是一个与点的位置有关系的变量。所谓拟合,就是求解该测区高程异常值的过程,其实质就是建立模型,解算出拟合方程的系数,这样如果知道一个点的坐标,就可以求出该点在该测区的高程异常值。GPS能够提供WGS-84坐标系下的精确三维坐标,通过坐标转换以后也能提供精度相当的平面坐标。而在高程方面,GPS高程能否达到等级水准测量的精度,还是人们探讨的一个课题。GPS测量得到的高是大地高,即地面点沿法线方向到参考椭球面的距离,这与我们常用的水准高程之间存在一个高程异常,为此,要通过GPS高程得到精度相对较高的水准高程就必须获得高精度的GPS大地高和当地的高程异常。

随着现代GPS接收机技术的发展和GPS数据处理软件的不断完善,相位整周模糊度解算、多路径效应的影响、电离层对三维坐标产生影响、天线高等影响GPS三维精度的因素可以有效减小[1],选择一个合适的方法和高程投影面,在范围不大的地区,GPS高程是可以到达相应等级水准测量的精度。

1 高程系统

高程测量是GPS测量的重要组成部分,在GPS相对定位中,所求得的三维基线向量,通过GPS网平差,可求得精密的WGS-84大地高差,再通过坐标转换,求得精密的国家或地区参考椭球的大地高差,如果已知网中一个或多个点的大地高程,就可以求得各GPS点的大地高。为了找出GPS高程系统与其他高程系统的关系,下面介绍几种常用的高程系统及它们的关系[2]。

1)大地高高程系:大地高高程系统是以参考椭球面为基准面的高程系统,地面某点的大地高程H定义为由地面点沿通过该点的椭球法线到椭球面的距离。GPS定位测量获得的是WGS-84椭球大地坐标系中的成果,也就是说GPS测量求得的是相对于WGS-84椭球的大地高程。由大地高程的定义可知,它是一个几何向量,不具有物理意义。不难理解,不同定义的椭球大地坐标系构成不同的大地高程系统。

2)正高高程系:正高高程系统以大地水准面为基准面的高程系统。地面上任一点的正高高程即该点沿垂线方向至大地水准面的距离,地面上某一点B点的正高可表示为

式中:gmB为B点到大地水准面的的垂线上的重力加速度的平均值,其值不能精确测定;∫gdh表示过B点的水准面与大地水准面间的位能差,不随积分路线而异。

3)正高高程的性质:

A.地面任一点的正高不随水准测量路线的不同而有差异,是唯一确定的值,可用来表示地面的高程;

B.由于gmB不能精确获得(包括测定及由公式推导),故严格来说,地面上任一点的正高高程不能精确求得;地面点的正高(H正)是该点至大地水准面的铅垂距离,也叫绝对高程或海拔。地面上某点的正高定义为由地面点沿铅垂线至大地水准面的距离。

4)正常高高程系:

正常高是将正高系统中不能精确获得的平均重力加速度gmB用正常重力γm B代替得到的另一种系统的高程;其公式表达为

式中:g可由沿水准测量路线的重力测量而得;γm B按正常重力公式算得的重力平均值,其数值不随水准路线不同而异,为唯一确定值;实际上,工程应用中所使用的正常高并不是依据上述方法计算得出,而是通过水准测量或通过高程转换获得。

正常高高程系统以似大地水准面为基准面的高程系统。在实际应用的高程测量中,地面点的高程采用正常高系统。地面点的正常高H是该点至似大地水准面的铅垂距离;而GPS所测高程为地面点沿通过该点的椭球法线到椭球面的距离,二者之间存在一个高程异常N,所以在使用时要把地面点的大地高H转换为正常高H正常。二者的关系为

式中:H表示大地高,N称为高程异常。我国规定采用正常高高程系统作为我国高程的统一系统。

2 GPS高程拟合模型及精度分析

GPS测量可以提供高精度的WGS-84坐标系下的大地高,但这不是我们使用的正常高。要将GPS大地高用于工程测量中,需进行高程的转换。目前,GPS高程转换到正常高的方法很多,如GPS三角高程﹑GPS重力高程﹑曲面拟合法﹑绘等值线图法﹑解析内插法等一系列方法。它们的转换方法不同,所能达到的精度也有差异[3,4],根据具体工程应用的条件和各种方法所能达到的精度,各种方法都在具体工程中得到了实践。在实际工程应用中最常用的是GPS水准法,即利用已知几何水准点或达到水准等级精度的高程控制点和GPS点联测,然后通过高程拟合实现GPS高程到正常高的转换,或通过这些数据拟合出测区所在区域的似大地水准面。

1)平面拟合模型及精度分析

平面拟合函数模型为

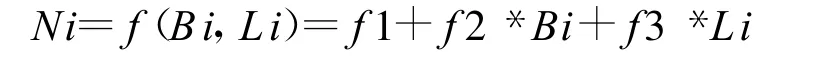
当已知点数大于3个时,可列出误差方程

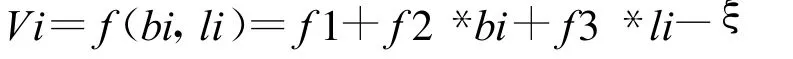
将上式写矩阵形式为

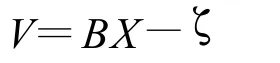
式中V=[v1,v2,v3]T

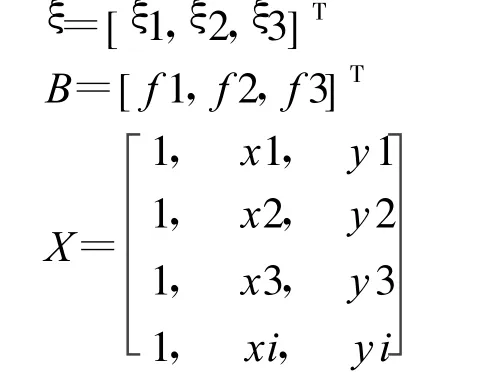
根据最小二乘原理,B=(XTX)-1Xξ,求得模型转换参数为

2)二次曲面拟合及精度分析

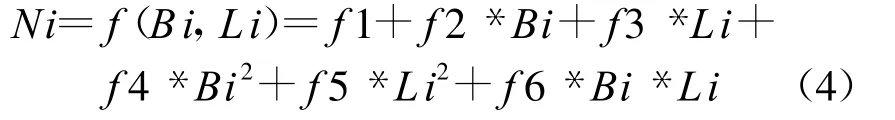
式中:f1,f 2,f 3,f 5,f6为模型参数。

当已知点数大于6个时,可列出相应的误差方程

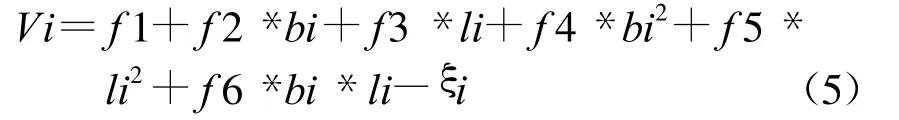
将式(5)写矩阵形式为

式中:

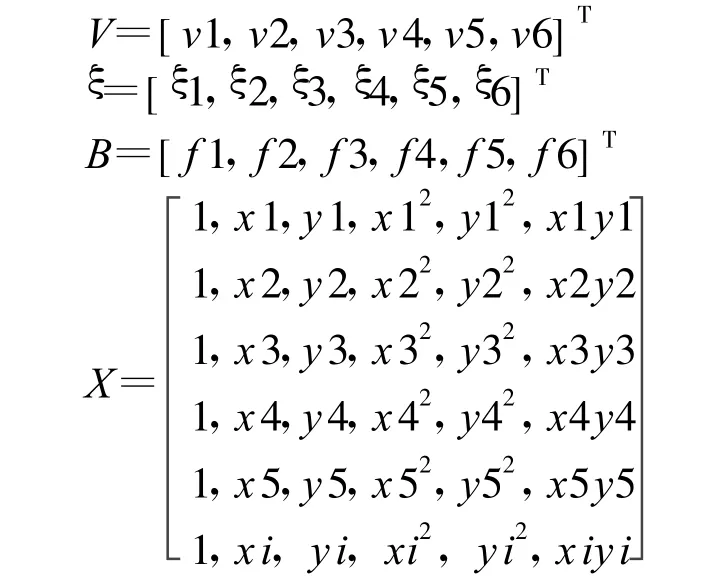
根据最小二乘原理,B=(XTX)-1Xξ。由观测数据根据以上模型求得模型转换参数为

为验证两种模型的可靠性和精度,依托大连地区二等水准网,选取了约14 km长的一段进行实验。本段共10个水准点,全部进行了二等水准测量。外业测量采用trimble 5800双频接收机进行观测,分别采用平面拟合跟曲面拟合模型进行计算,计算结果和二等水准测量成果进行对比。为了客观地反映两种模型拟合的精度,对拟合后的高差进行比较,以相应等级的水准测量的闭合差限差为标准,结果如表1、2所示:

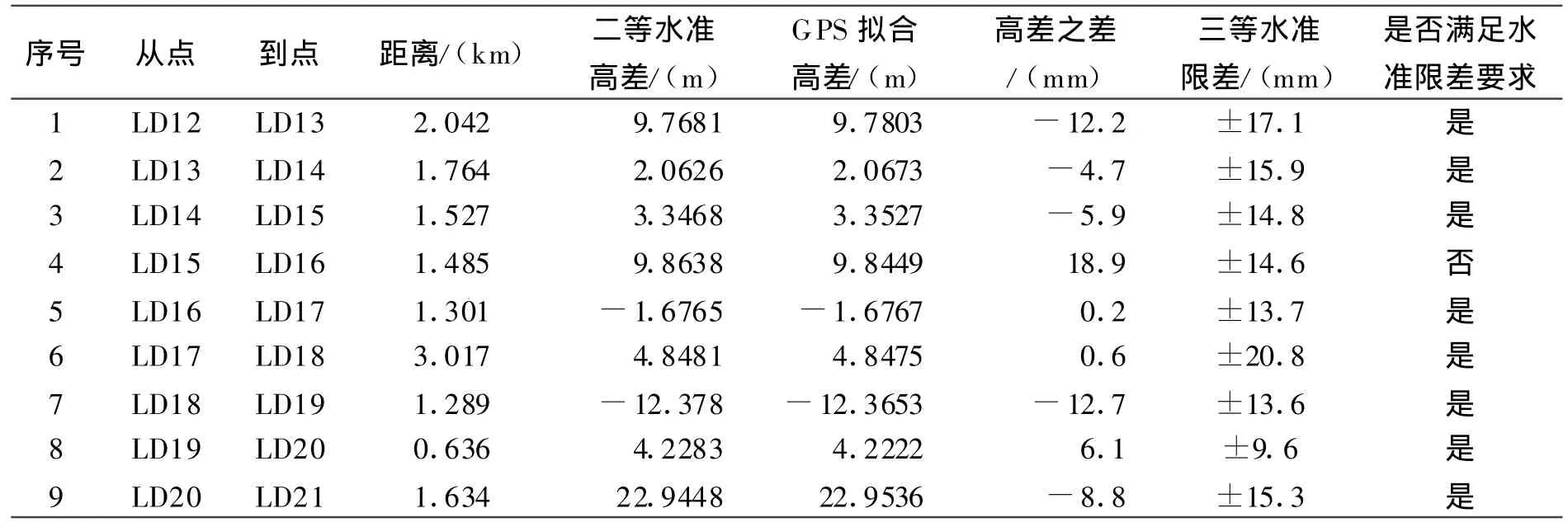
表1 平面模型拟合高差比较表

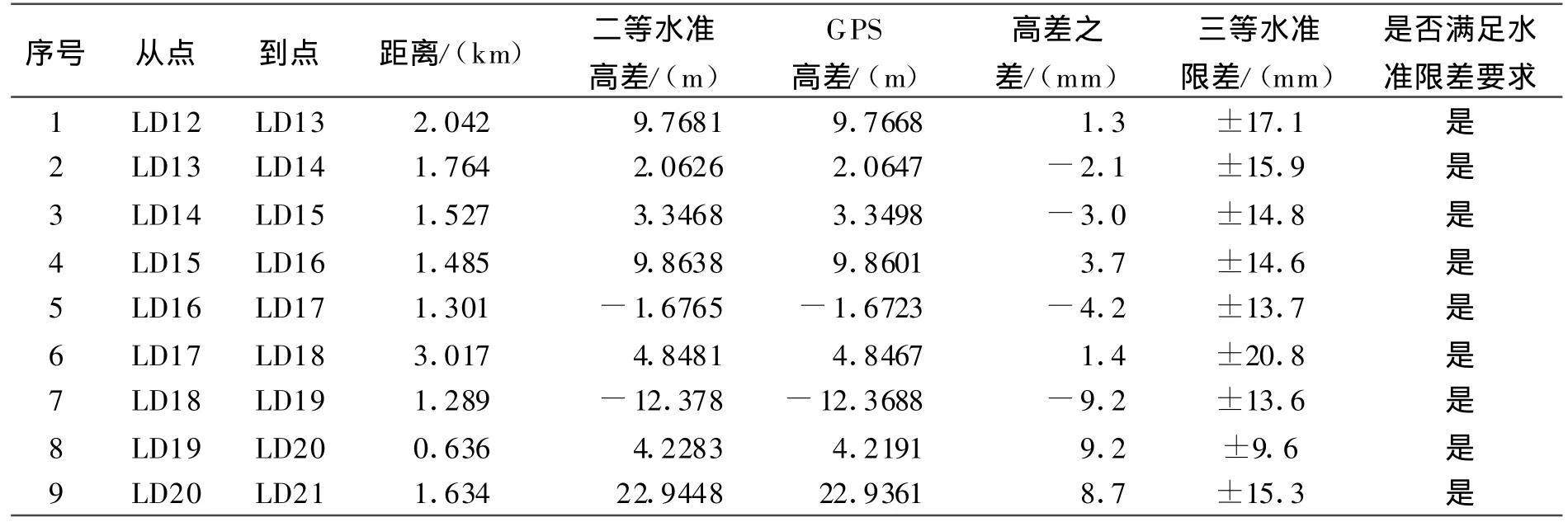
表2 二次曲面模型拟合高差比较

从表1和表2可以看出,比较GPS拟合高差和二等水准测量高差,以相应等级的水准测量的闭合差限差为标准,统计和实验结果显示:同样是二次曲面拟合精度要高于平面拟合精度;而且,二次曲面拟合精度是能够达到三等水准测量的精度。需要特别指出的是,平面拟合精度虽然达不到三等水准测量精度,但是代替四等水准测量,精度还是有保证的。

3 结 论

GPS测量已能够提供毫米级的平面坐标,但因似大地水准面与参考椭球面的差距,使得高精度的GPS大地高不能直接运用于生产实践。如何将GPS大地高转化成水准高程,并使其保持一定的精度,一直是人们研究的热点。随着现代GPS技术硬件和软件和不断完善及数据处理方法的改进,人们在GPS高程拟合方面做了大量的工作,根据本人的工作实践,得出以下几点经验:

1)在小范围内,地势起伏不是很大的地区,选择合适的数学模型,GPS高程拟合可以达到三等水准测量的精度;

2)已知点的选取对拟合的精度影响很大,因此已知点应该尽量选取均匀点位;

3)采用相同的拟合方法,起算点数量越多、分布越均匀,则拟合精度越高,但也并非总是如此,对含有不同地形趋势的大测区,应采用分区计算的方法;

4)由于高程异常的确定不仅取决于地球内部的密度变化,还取决于地形起伏等各种因素。因此,用一种数学函数去拟合测区内给定的高程异常点,其模型误差是不可避免的,选取模型误差较小的拟合方程来描述其高程异常分布只是一种相对合理的方法。

[1] 徐绍铨 ,张华海 ,杨志强等.GPS测量原理及应用[M].武汉:武汉大学出版社,2006.

[2] 孔祥元 ,梅是义.控制测量学[M].武汉:武汉大学出版社,2002.

[3] 熊小莉,吴迪军.GPS高程拟合模型的精度分析[J].铁道勘测,2007,15(2):27-28.

[4] 伍青云 .GPS高程拟合的方式及可靠性分析[J].现代测绘,2006,29(4):29-31.