智能电器控制板EMC仿真与优化

唐 骏 陈丽安 孙 园

（厦门理工学院电子与电气工程系，福建 厦门 361024）

1 引言

电磁兼容性反映了电子或电气设备/系统在其电磁环境中符合要求地运行且不对其环境中其他任何设备产生无法忍受的电磁干扰的能力[1]。智能电器是传统电器与电子技术结合的产物，目前，以智能电器为基础的大型电力设备的在线监测，对于电力系统的安全运行更是起着至关重要的作用， 由于智能电器经常运行于高电压、大电流的现场环境中，与被保护和监控的设备、系统处于同一个电磁空间，以微型计算机为核心的监控单元必然会受到来自于电力系统的不同能量、不同频率的电磁干扰，因此，智能电器的电磁兼容问题集中在智能电器的控制单元上。智能电器的电磁兼容性能直接关系到智能电器的可靠工作，进而对电力系统的安全运行造成影响。与智能电器功能与原理的研究相比较，EMC问题的研究显得严重不足：在产品的设计过程中，不能针对 EMC问题系统地考虑元件性能的选配和系统结构的整合；某个 EMC问题的解决经常要经过反复的试验和修改，并且往往不能对出现 EMC问题的范围进行准确的定位，对该设计可能出现的EMC风险不能给出科学的预测。在设计时有一定的盲目性，往往存在过度设计和设计不足的问题，由此提高了成本、延长了开发周期。

最经济有效的电磁兼容设计方法是在设计的早期阶段充分考虑电磁兼容的技术要求，从国际上来看，电磁兼容仿真己经成为电子设备设计时必须的一个步骤，通过仿真可以在设备投入生产之前发现问题、解决电磁兼容问题，从而节省由于电磁兼容不达标造成反复修改设计的成本[2]。本文采用SIwave仿真软件，在智能电器控制板设计阶段，通过设计——仿真——优化——仿真的方法，在产品成型之前很好地解决了EMC问题。

2 电磁兼容仿真的基本方法

大体而言，电磁问题的计算方法可分为三类：理论分析法、专家系统及数值分析法。理论分析法对问题的几何模型做简化和假设，从而得到近似解。专家系统对场不进行精确分析，它根据自身数据库，来估算相应的参数值。而数值方法设法求解带有相应边界约束条件基础的场方程(麦克斯韦方程组)，对场进行精确地分析。由于数值方法的精确性，因而此方法在工程中得到了广泛的应用。

电磁兼容数值仿真过程也就是电磁场问题的数值计算过程。在求解电磁场边值问题的过程中，如果数学模型是齐次或非齐次偏微分方程，则只有对于简单媒质和边界条件的少数问题，才能由解析方法得到精确解。电磁波散射和衍射问题的数学模型是积分方程，求解过程中的计算量非常大，所以在过去计算机存储容量和运算速度都十分有限的情况下，要得到解析解是很困难的[3]。随着高速大容量电子计算机的迅速发展，利用计算机进行多维数值积分、高阶矩阵求逆等运算己成为可行。自上世纪六十年代中期开始，计算机技术在求解导行波、天线和散射等实际电磁场问题的数值计算中得到了广泛应用。到目前为止，电磁场数值分析方法在解决有关电磁兼容方面问题起到了非常重要的作用，80%的电磁兼容问题都能利用仿真在设计阶段予以解决。数值分析方法则是把连续变量函数离散化，把微分方程化为差分方程，把积分方程化为有限求和的形式，从而建立收敛的代数方程组，然后利用计算机分步进行求解。为了精确分析在某一空间范围内随时间变化的电磁场，可能需要无限多个数据。但是，一方面，由于数字计算机可处理数据的字长和存储容量的有限性使其无法存储太多的数据，另一方面，运算速度的有限性使其在有限时间内难以得出对象的精确解，所以实际应用中必须作些近似和简化。目前计算电磁场的数值方法有变分法、时域有限差分法、矩量法、有限元法、边界元法等，其中变分法是这些方法的基础。电磁兼容数值仿真商用软件较多，主要有ANSOFT、CST Microwave Studio、 ANSYS(FEKO)、FLO/EMC、EMC2000、IES等。

3 仿真工具选择

EMC仿真软件能够为我们提供非常有效的高频和高速电磁仿真设计工具，它集高速电路建模、仿真和优化为一体，用仿真代替实验，可以快速的帮助工程师完成高速电路EMC设计，实现信号完整性，减少研发费用，缩短研发周期。目前，国际上商业的EMC仿真软件有许多种，主要应用于高速PCB电路设计、各种类型的高频滤波器设计、高频天线和波导设计、传输线设计（包括微带、带状线和同轴电缆等）、信号完整性设计和电磁分析等。此外，不同仿真软件对模型的要求也各不相同。根据智能电器控制板的特点，我们选用Ansoft SIwave作为仿真工具，该软件是一个精确的整板级电磁场全波分析工具，它采用三维电磁场全波方法分析整板或整个封装的全波效应。板上放置去耦电容的作用，改变信号层或分开供电板引入的阻抗不连续性；信号线与供电板间的噪声耦合、传输延迟、过冲和下冲、反射和振铃等时域效应；本振模和S、Z、Y参数等频域现象。其结果可以先进的二/三维方式图形显示，并可输出Spice等效电路模型用于Spice仿真。 SIwave提供了无缝的集成设计流程，可以从标准布板工具如，Cadence Allegro、APD、Zuken CR-5000等所产生的版图直接输入到SIwave中进行分析。

4 仿真结果及分析

为了减小电源/地弹噪声和EMI辐射，该智能电器控制板采用了多层PCB板结构，此结构使得电源平面和地平面耦合更紧，同时可以严格控制阻抗以防止信号回路问题。但多层板结构会引起较严重的电源完整性问题，地层和相邻的电源层形成波导结构，该结构的谐振模式取决于结构的几何形状、尺寸以及叠层的介质，由于谐振将导致严重的开关噪声，因此，谐振模式的仿真必须在设计的前期进行[4-5]。

用SIwave软件对控制板的PCB进行仿真分析。对于真实复杂的PCB板或IC封装，包括多层、任意形状的电源和信号线，SIwave可仿真整个电源和地结构的谐振频率。针对该控制板，在频率120MHz～1.2GHz范围内，共计算10个谐振模式，如图1所示。

图1 谐振模式

在每一谐振模式下，整个板的电压分布都能以三维图形加以显示，比较发现，在模式 2和模式8下，谐振最为严重，电压分布如图2和图3所示。

图2 模式2的电压分布

图3 模式8的电压分布

图4 放置去耦电容

控制板要尽可能避免工作在谐振频率点，如果无法回避，则可以通过在PCB板上放置去耦电容改变谐振频率[6]。阻抗与电容值满足如下关系式：

其中，cZ是阻抗，C是电容值，ω是工作频率。在谐振较严重的区域共放置 21只去耦电容，如图 4所示，在相同的频率范围内重新计算谐振模式，结果表明，在120MHz～1.2GHz内只有一个谐振模式，如图5所示，与之对应的电压分布如图6所示。结果表明，去耦电容改变了谐振频率，从而实现控制板的工作频率远离谐振频率，进而改善EMC性能。

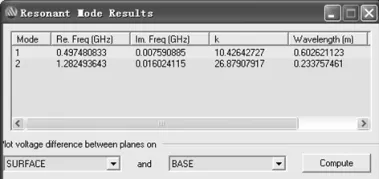
图5 谐振模式

图6 优化后的电压分布

5 结论

利用仿真的方法在电子设备设计之初解决EMC问题具有重要意义。本文介绍了EMC仿真的基本方法，并借助优秀的电磁仿真软件SIwave对智能电器控制板进行了 EMC仿真分析。该控制板的特点是电源系统较复杂，由开关电源提供三种不同特性的电源，由于高速PCB的信号完整性、电源完整性与电磁兼容直接相关，因此，良好的电源完整性有利于信号完整性和电磁兼容，依据这一事实，对电源完整性的仿真作为该系统 EMI/EMC分析的重点。仿真分为两个阶段：优化前仿真与优化后仿真。由于去耦电容可以改变谐振频率，因此优化的主要手段是在必要的区域合理地放置去耦电容。仿真结果表明，通过优化设计，PCB表面电压明显减小，有效地抑制了辐射，从而改善EMC性能。

[1] T. Steinecke, M. Schmidt, H. Köhne, W.John. EMC Modeling and Simulation on Chiplevel[C]. IEEE Customer Service, IEEE International EMC Symposium, Montreal, 2001：1191-1196.

[2] J.-J. Laurin, S. G. Zaky, and K. G. Balmain. On the prediction of digital circuit susceptibility to radiated EMI[J]. IEEE Transactions on Electromagnetic Compatibility, 1995, 37(4)：528-535.

[3] 王长清.现代计算电磁学基础[M]. 北京：北京大学出版社，2005.

[4] Mohamed Ramdani, Etienne Sicard and Alexandre Boyer. The Electromagnetic Compatibility of Integrated Circuits—Past, Present, and Future[J]. IEEE Transactions on Electromagnetic Compatibility, 2009, 51(1)：78-100.

[5] Han Yi-feng, Yan Zhao-wen. The Simulation and Pre-design on the PCB of the Simulator[C]. Electromagnetic Compatibility and 19th International Zurich Symposium on Electromagnetic Compatibility. Singapore, 2008：871-874.

[6] Pingqiang Zhou, Karthikk Sridharan and Sachin S. Sapatnekar. Optimizing decoupling capacitors in 3D Circuits for Power Grid Integrity[J]. IEEE Design and Test of Computers, 2009, 26(5)：15-25.