航班进场调度的改进捕食搜索算法
姜 雨 杨英宝 周 航
(南京航空航天大学民航学院,南京,210016,中国)
INTRODUCTION
Over the past few decades, arrival sequencing and scheduling(ASS)has been one of majorissuesin the research ofair traffic management.Ref.[1]showed arrival planning plays an important role in the free flight concept.Researchers all over the world have gained plenty of achievements on ASS problems.J E Beasley,et al gave an extensive literature review on the ASS problem[2]. Some typical ones are listed below.
To minimize the deviation from the preferred arrival time or the total timespan, J Beasley,et al[2-4]gave a mixed integer programming formulation considering both single and multiple runway systems,and they used several heuristic algorithms to solve the problem,such as branch and bound algorithm[2]and genetic algorithm[4].C C Gregory,et al analyzed the effect of using sequence preference in terms of airlines[5]and exchanging delays[6]. M J Soomerand G J Franx[7]introduced collaborative decision making in the ASS problem,and minimized the delay cost determined by cost functions related to each aircraft. Although there are some differences among ASS models,the main ideas of different ASS models are similar.Despite of single runway ormultiple runways, the objective ofASS problems in most literatures is to minimize the total delay time of arriving flights.Literatures with other objectives are less seen[7].Therefore,many researchers have been devoted to improving the algorithm to solve the ASS problem.As is well known,the ASS problem is a NP-hard problem,which has no well-known algorithm for finding global optimal solution within a polynomial-bounded amount of time[8].In past few years,a variety of intelligent algorithms had been developed for solving the ASS problem[9-15].
Predatory search algorithm(PSA)is a new bionic computationalmethod proposed by A Linhares in 1998[16].PSA imitates the predatory action of animals,and performs local search,global search,and their transfering to each other by changing the solution space of search. It performs well in local search,escaping from local optimal.It is applied to combination optimization problems,such as T SP[17],VLSI layouts[18],and vehicle routing problems[19].Nevertheless,the study on PSA is still less seen in report[19].Like other intelligent algorithms,PSA also has some shortcomings.For example,the occurrence that PSA may find the better solutions found in the previous time wastes time and results in bad solutions[17]. Furthermore, PSA is efficient in solving the problems,of which the local optimal solutions gather near the global optimal solution.When the local optimal solutions scatter in the solution space,predatory search is inefficient[18].The performance of PSA mainly relies on the transferring between localsearch and global search. The paper is devoted to designing an innovative PSA with variable constraints of local search and global search.
1 ASS MODEL
Since the ASS problem has been studied for years,the models for both single runway and mutiple runways are nearly regular.The models can be used to determine an arrival sequence and arrival times on a single runway for a given set of flights,complying with the separation minima.Besides,the models can be used to assign arriving flights to different runways at the airport with multiple runways.Then,the typical model is described below[2].For an airport with r(r≥1)runway(s)R= {R1,…,Rr},there is n arriving flights during a certain period,that is F= {F1,F2,…,Fn}.For a runway∀Rj∈ R,Ej={Ej(1),Ej(2),…,Ej(n)}(1≤j≤r)is the set of the estimated arrival time for each flight when all flights are assigned to runway Rj.Aj(i)is the the assigned arrival time for∀Fi∈F if Fiis assigned to runway Rj.One flight should only be assigned to one runway.For two close flights assigned to the same runway, that is Fiand Fi-1, the separation minimum between them is denoted as T(i,i-1).To minimize the total delay time of arriving flights,the model can be written as
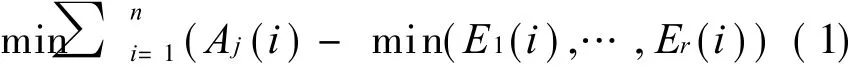
Subject to

Eq.(2)ensures that the separation between two close flights assigned to the same runway complies with the separation minima. Eq.(3)indicates that the assigned arrival time should not be earlier than the estimated arrival time.
2 INNOVATIVE PSA
2.1 Introduction of PSA
When predatory animals prey,they quickly search for prey in the living space.If they find prey or the tracks of prey,they will concentrate on the area near prey or their tracks.If prey is not found,they will continue to search the whole space.Imitating the preying strategy,Ref.[18]proposed PSA. PSA firstly performsglobal search in the solution space until a better solution is found.Then,local search is not performed near the solution for set times until no better solutions are found.After local searches,PSA performs global search again.The cycle continues until the global optimal solution or approximately global optimal solutions are found.Due to the limited space for local search,it can obtain a higher speed of search.Global search can avoid falling into local optimal solutions.
Some parameters used in PSA are defined as follows:
LEVEL-NUM:the total constraint;
LOCAL-LEVEL: the constraint of local search;
GLOBAL-LEVEL:the constraint of global search;
COUNTER-M AX:maximum cycling times in each constraint;
N: the times of searching the current neighborhood;
f(x):the objective function;
xmin:the optimal solution till now;
Level:the level of the restriction;
Counter:the times of cycling.
The steps of PSA are listed as follows[19]:
Step 1 Generate an initial solution x randomly.Make xmin=x,Level=0,and Counter=0.
Step 2 If Level≤ LEVEL-NUM,then search the neighborhood of x for N times,gain the minimal solution xn min,and turn to Step 3.Otherwise,terminate,and xminis the optimal solution.
Step 3 If f(xn min)≤ Restriction(Level),then x=xnmin,and turn to Step 4.Otherwise,turn to Step 5.
Step 4 If f(x)<f(xmin),then make xmin=x,Level= 0,and Counter= 0.Compute the restrictions again,and turn to Step 2.Otherwise,turn to Step 5.
Step 5 Make Counter= Counter+ 1.If Counter> COUNTER-M AX,make Level=Level+1 and Counter= 0,and turn to Step 6.Otherwise,turn to Step 2.
Step 6 If Level=LOCAL-LEV EL,then make Level= GLOBAL-LEVEL,and turn to Step 2.Otherwise,turn to Step 2.
Once xmin is gained,the operations below are performed to compute the restrictions:
Step 1 Search the neighborhood of xminfor LEVEL-NUM times,and gain LEVEL-NUM values of the objective function.
Step 2 Range the LEVEL-NUM values and xminin a ascending order.
Step 3 Successively assign the LEVELNUM+ 1 values to Restriction(0),Restriction(1),…,Restriction(LEVEL-NUM).
Step 4 Set Restriction(0),Restriction(1),…, Restriction(LOCAL- LEVEL)as the restrictions of local search,and set Restriction(GLOBAL-LEV EL),…,Restriction(LEVELNUM)as the restrictions of global search.
2.2 Improvement
PSA transfers local search into global search through the change of Level in Step 6.We can see that the constraints of local search and global search used in typical PSA are constant. To ensure that PSA performs steadily,the constraint oflocal search should be smaller,and the constraint of global search should be larger at the initial time.Later,the constraint of local search should be larger,and the constraint of global search should be smaller to avoid degeneration and local optimal solutions.Of the new PSA,the constraints of local search and global search change as the algorithm is performed,and they are formulated as

where k is the times for which the global search is performed.GLOBAL-LEVELmaxand GLOBALLEVELminare the maximum and the minimum constraints of global search, respectively,LOCAL-LEVELmaxand LOCAL-LEVELminthe maximum and the minimum constraints of local search,respectively.Then GLOBAL-LEVELk and LOCAL- LEVELk are substituted for GLOBAL-LEV ELandLOCAL-LEVEL in typical PSA,respectively.
2.3 Operationsof coding solutions and neighbourhood generating
The integersequencesare used to code solutions, thatis, randomly two group of integers are generated to represent the arrival sequence and the runway allocated to each flight if there are more than one runways.For example,there is a code of
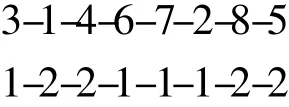
where the upper group of integers represents the arrival sequence from flight one to flight eight,and the lower group of integers the runways allocated to the corresponding flights in the upper group if there are two runways.To generate the neighbourhood of a solution,we randomly choose two integers of either group of the code,and reverse the part of the code between them.The neighbourhood should be checked according to the constraints of the model,and invalid solutions should be excluded before the algorithm is performed.
2.4 Case study
To test how well the new PSA may be applied in real world,we perform numerical tests based on the data of Ref.[13],where there are two runways R= {R1,R2}and ten arriving flights.Since the flights arrive during an hour,the estimated arrival time for landing in R1and R2with the hour being omitted is noted as E1={11,15,6,6,9,7,15,6,6,9}and E2={10,17,7,7,12,6,17,7,7,12}.The types of the flights are{H,L,H,H,S,H,L,H,H,S}. The wake separation minima are shown in Table 1.
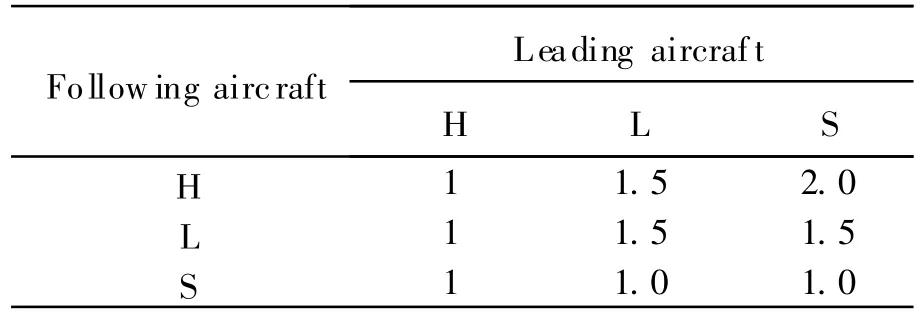
Table 1 Wake separation minima
The separation T(i,i-1)is determined by the types of two close aircraft according to Table 1,where the head row represents the types of leading aircraft,and the left column represents the types of following aircraft.The parameters used in the new PSA are set as follows:N=5,LEVEL-NUM=10,LOCAL-LEVELmin= 2,LOCAL-LEV ELmax=5,GLOBAL-LEV ELmin=6, GLOBAL- LEVELmax= 8, COUNT ERMAX=80.Choose R1as an example to test the algorithm,and the results are shown in Table 2,as well as the results of using first come first serve(FCFS).

Table2 Test results on runway1
It can be seen from Table 2 that the total delay time gained by using FCFS and the new PSA are 21.5 min and 19.5 min,respectively.The case of double runways is studied and the results are shown in Table 3.
It can be seen from Table 3 that the total delay time gained by using FCFS and the new PSA are 12.5 min and 6.5 min,respectively.The results are the same as the ones in Refs.[13-14].It is known that computational complexity in the case of mutiple runways is much larger than that of single runway.To test how efficiently the new PSA will perform,the new PSA,the typical PSA and the genetic algorithm(GA)are apply in the case of double runways for 20 times to compare the performance of the new PSA with that of both typical PSA and GA.The parameters used in the typical PSA are the same as the ones used in the new PSA except that LOCAL-LEVEL=3 and GLOBAL-LEVEL=7.The parameters and rules used in GA are set as follows.The rule of coding solutions is the same as the one mentioned above.The fitness function is the objective function.The population is 100. The selection of solutions complies with the method ofroulette. The probabilities of crossing and mutation are 0.8 and 0.01,respectively.The maximum generation is 100.The total delay time gained by the three algorithms are listed in Table 4.
Although the three algorithms can gain the same optimal solution,it can be seen from Table 4 that the rates of GA,typical PSA and new PSA gaining optimal solutions are 60%,85% and 95%, respectively. Furthermore, the average computational time of GA,typical PSA and new PSA is 3.23,2.34 and 2.08 s,respectively.
3 CONCLUSION
The paper designs an innovative PSA with variable constraints of local search and global search to solve the ASS problem more efficiently.Variable constraints of local search and global search could contribute to avoiding falling into local optimal solutions and degeneration of solutions.Test results show that the new PSA performs much better than typical PSA as well as GA in solving the ASS problem in the aspects of the rate of gaining optimal solutions and the computational time.As a new bionic algorithm,PSA has a large potential for being improved.How to guide the transferring between global search,and local search and effectively change the neighborhood ofsearch, willbe worth studying.The applications of PSA in engineering also need studying.Further research on the ASS problem will be conducted by considering more about uncertain conditions, such as weather,congestion and airspace restriction.And the ASS models and algorithms would be modified and improved.
[1] Andreatta G,Brunetta L, Guastalla G. From ground holding to free flight:An exact approach[J].Transportation Science,2000,34(4):394-401.
[2] Beasley J E,Krishnamoorthy M,Sharaiha Y M,et al.Schedulingaircraft landings-The static case[J].Transportation Science,2000,34(2):180-197.
[3] Beasley J E,Krishnamoorthy M,Sharaiha Y M,et al. Displacement problem and dynamically scheduling aircraft landings[J]. Journal ofthe Operational Research Society,2004,55(1):54-64.
[4] Beasley J E,Sonander J,Havelock P.Scheduling aircraft landings at London Heathow using a population heuristic[J].Journal of the Operational Research Society,2001,52(5):483-493.
[5] Gregory C C,Erzberger H,Neuman F.Airline arrival prioritization in sequencing and scheduling[C]//the 2nd U SA/EUROPE Air Traffic ManagementR&D Semminar.Orlando:[s.n.],1998.
[6] Gregory C C,Erzberger H,Neuman F.Delay exchanges in arrival sequencing and scheduling[J].Journal of Aircraft,1999,36(5):785-791.
[7] Soomer M J,Franx G J.Scheduling aircraft landings using airlines′preferences[J].European Journal of Operational Research,2008,190(1):277-291.
[8] Bianco L,Dell′Olmo P,Giordani S.Modelling and simulation in air traffic management[M].Berlin:Springer,1997.
[9] Hu X B,Chen W H.Receding horizon control for aircraft arrival sequencing and scheduling[J].IEEE Transaction on Intelligent Transportation System,2005,6(2):189-197.
[10]Gregory C C,Erzberger H,Neuman F.Fast-time study of aircraft-influenced arrival swquencing and scheduling[J].Journal of Guidance,Control and Dynamics,2000,23(3):526-531.
[11]Bianco L,Bielli M M.Large scale computation and information processing in air traffic control[M].Berlin:Springer,1993.
[12]Robinson III J E,Davis T J,Issacson D R.Fuzzy reasoning-based sequencing of arrival aircraft in the terminal area[C]//The AIAA Guidance,Navigation and Control Conference.New Orleans,LA:[s.n.],1997.
[13]Xu Xiaohao,Yao Yuan. Application of genetic algorithm to aircraft sequencing in terminal area[J].Journal of Traffic and Transportation Engineering,2004,4(3):121-126.(in Chinese)
[14]Wang Fei,Xu Xiaohao,Zhang Jing.Mixed artificial fish schoolalgorithm ofaircraft sequencing in terminal area [J]. Journal of Traffic and Transportation Engineering,2008,8(3):68-72.(in Chinese)
[15]Hu X B,Paolo E D.An efficient genetic algorithm with crossover for air traffic control[J].Computers&Operations Research,2009,36(1):245-259.
[16]Linhares A.Preying on optima:A predatory search strategy for combinatorial problems[C]//the IEEE International Conference of Systems, Man and Cybernetics.San Diego:[s.n.],1998:2974-2978.
[17]Linhares A.State-space search strategies gleaned from animal behavior: A traveling salesman experiment[J].Biological Cybernetics,1998,78(3):167-173.
[18]Linhares A.Synthesizing a predatory search strategy for VISIlayouts[J]. IEEE Transactions on Evolutionary Computation,1999,3(2):147-152.
[19]Jiang Zhongzhong,Wang Dingwei.Predatory search algorithm for vehicle routing problem with time windows[J].Control and Decision,2007,22(1):59-62.(in Chinese)
 Transactions of Nanjing University of Aeronautics and Astronautics2010年4期
Transactions of Nanjing University of Aeronautics and Astronautics2010年4期
- Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- 染料敏化太阳能电池用聚偏氟乙烯 /丙烯酸酯互穿网络基凝胶聚合物电解质的制备与性能表征
- 纳米二氧化钛吸入对小鼠肺部和血清生化指标的影响
- 飞机除冰液对高性能混凝土抗冻性的影响
- 微型叶轮机械联合试验台设计
- 机身整体壁板在轴压载荷下后屈曲计算及结构优化
