一种基于曲波变换的遥感图像融合新算法
满 旺,袁 莹,黄于同 (厦门理工学院空间信息科学与工程系,福建厦门361 024)
张杰林 (核工业北京地质研究院遥感信息与图像分析技术国家级重点实验室,北京1 00029)
随着遥感技术的迅猛发展,多种类型传感器相继投入使用,人类获取了大量的全色、多光谱、高光谱、雷达及热红外等各种类型的遥感影像。由于成像原理不同和技术条件的限制,单一图像数据往往不能全面反映目标地物的全部特征。遥感图像融合能够集成或整合多个图像中的冗余信息和互补信息,利用优势互补的数据来提高图像的信息可用程度,可增加对研究对象解译的可靠性。因此,遥感图像融合一直是遥感研究领域的研究热点[1,2~6]。
遥感图像融合可分为像素级图像融合、特征级图像融合及决策级融合等3个层次[1,2],其中像素级融合研究最为活跃。常见的像素级融合方法包括Brovey变换、PCA变换、IHS变换及基于多分辨率分析的各种方法。小波作为典型的多分辨率分析工具在图像融合中曾广受关注,但小波在表达图像边缘的方向特性上存在缺陷。曲波变换正是在研究小波变换的基础上发展起来的。曲波变换具有良好的边缘提取能力,能够将遥感图像分解到一系列不同频率信道中。然后利用其分解后的结构,对不同层、不同方向频带的分解系数按照不同的融合规则进行处理,通过逆曲波变换,得到融合后图像。因此,基于曲波变换的图像融合正成为当前研究的热点。张强等[7]对IKONOS全色与多光谱影像进行了融合研究;蒋年德等[8]将曲波变换同IHS变换结合进行图像融合;许星[9]、李晖晖等[10]分别使用曲波变换对SAR与TM进行融合研究;付梦印等[11]使用曲波变换对红外与可见光进行融合;邱宣等[12]将邻域方差加权平均引入融合规则;赵诚等[13]提出粒子群优化的图像融合方法。笔者首先简述了小波变换和曲波变换,然后提出了基于曲波变换的SPOT与TM影像融合算法,并与其他传统算法从多方面进行了比较。试验结果表明,使用曲波变换进行图像融合,能够取得较好的效果。
1 小波变换和曲波变换
小波变换是空间和频率的局部变换,因而能有效地从信号中提取信息。通过伸缩和平移等运算功能可对函数或信号进行多尺度的细化分析。对于含 “点奇异”的一维信号,小波能达到 “最优”的非线性逼近阶。而在处理二维或者更高维含 “线奇异”的信号时,虽然由一维小波张成的高维小波基在逼近性能上要优于三角基,但是小波变换并不能充分利用图像本身特有的几何特征,并不是最优的和 “最稀疏”的函数表示方法,不能达到理想的最优逼近阶[3]。
Candès等[4,5]提出了一种适合分析具有曲线或超平面奇异性高维信号的曲波变换,曲波变换也是一种多尺度变换,其框架元素以尺度、位置为参数,同时还包含了方向参量。因此,曲波变换具有比小波变换更强的方向选择和辨识能力,能够更好的表达遥感图像的空间几何特征,关于曲波变换的理论见参考文献 [5]。
2 曲波变换稀疏表达能力试验
相对于小波而言,曲波变换具有更好的稀疏表达能力,它能将遥感图像的边缘及其他线性几何特征用较大的曲波系数表达出来,变换后能量更加集中。因此非常有利于提取高分辨率遥感影像中的几何信息。为测试曲波变换的稀疏表达能力,笔者设计了一组试验,分别用最大0.1%、1%、10%、20%的曲波系数,进行曲波逆变换,得到Lena图像。恢复效果如图1所示。分别计算了同原图像的相关系数,发现仅用最大0.1%的系数恢复的Lena的图像,与原相关图像的相关系数达到了 0.81;用最大 10%的系数恢复的 Lena图像,在目视效果上已经和原图像相差不大;用最大20%的系数恢复的图像,与原图像相关系数达到了0.9985。因此,曲波变换在图像压缩、图像去噪等方面具有良好的应用前景。

图1 曲波系数表达能力试验组图
3 基于曲波变换的图像融合算法
遥感图像进行曲波变换后,能量更多集中在曲波变换系数中,将高空间分辨率的全色遥感影像的高频边缘信息注入到低空间分辨率多光谱遥感图像中,理论上应该能有效提高多光谱影像的空间分辨率。基于以上设想,笔者提出了一种遥感图像融合新算法:
1)分别对融合源图像进行配准;
2)对融合图像按波段分别进行n级曲波变换。TM每波段影像变换后,系数为其中,TM代表TM影像;b为波段号;n为分解层级;l为分解方向;(i,j)表示像素坐标;表示TM影像中b波段的低频子带系数,表示TM影像中b波段的高频子带系数。为SPOT影像分解后曲波系数为SPOT影像曲波分解后的低频子带系数,为高频子带系数。
3)采用一定的融合规则,对曲波变换后系数进行处理。对图像进行曲波变换后,图像的边缘等几何信息集中在曲波变换的高频子带系数中,其绝对值越大,能量越集中。将曲波变换后的高频信息注入到低分辨率图像中,能有效提高其分辨率。笔者进行了3层曲波变换分解。为融合图像的低频子带的曲波系数,对于低频部分,直接取为高频子带的曲波系数,对于每一层高频子带,取
曲波变换可以对图像进行多层分解,但对于遥感图像数据融合来讲,分解多少层为宜?笔者分别对待融合图像进行2~6层分解,进行融合试验,发现随着分解层次的提高,信息熵和等效视数减小[10];相关系数、灰度变换指数以2到3层为最佳;空间频率以3层为佳。综合来看,基于曲波变换的图像融合,分解层次以2到3层为宜。
4 图像融合效果评价
为了了解新算法的性能,分别将其与采用Brovey变换、PCA变换和小波变换3种图像融合算法进行对比,融合图像分别采用SPOT与TM影像。笔者采用的融合试验数据为Envi4.6所带的伦敦地区部分示例数据,其中TM空间分辨率为28m,采用其中3个波段;SPOT空间分辨率为10m,为全色波段。原始图像信息见表1,原图及融合后图像见图2。
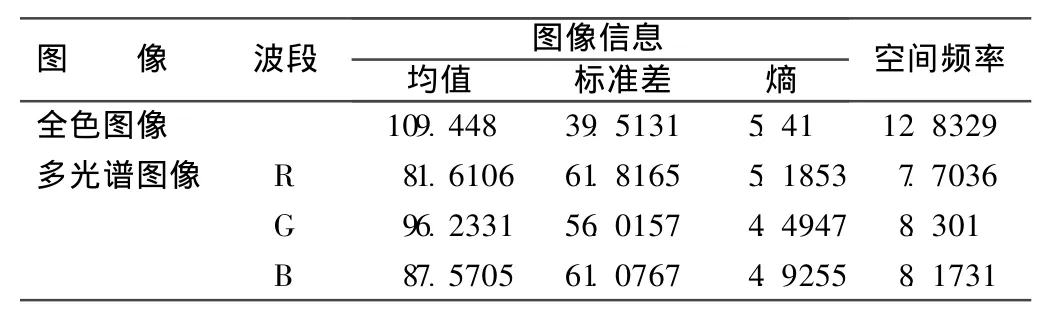
表1 全色图像及多光谱图像信息表

图2 各种融合算法对多光谱图像处理效果图
当前的图像融合质量评价中,并没有统一的评价体系,笔者分别从信息熵、光谱扭曲程度和图像空间频率3个方面进行评价,具体指标参见表2所示。
从表2可以看出,在信息熵方面,新算法略优于小波算法,Brovey变换算法表现最差,各波段信息熵明显小于其他方法;在光谱扭曲程度上,Brovey变换>PCA变换>小波变换>新算法;在空间频率上,以PCA变换为最优,新算法略微落后于前3种算法,但劣势并不明显。
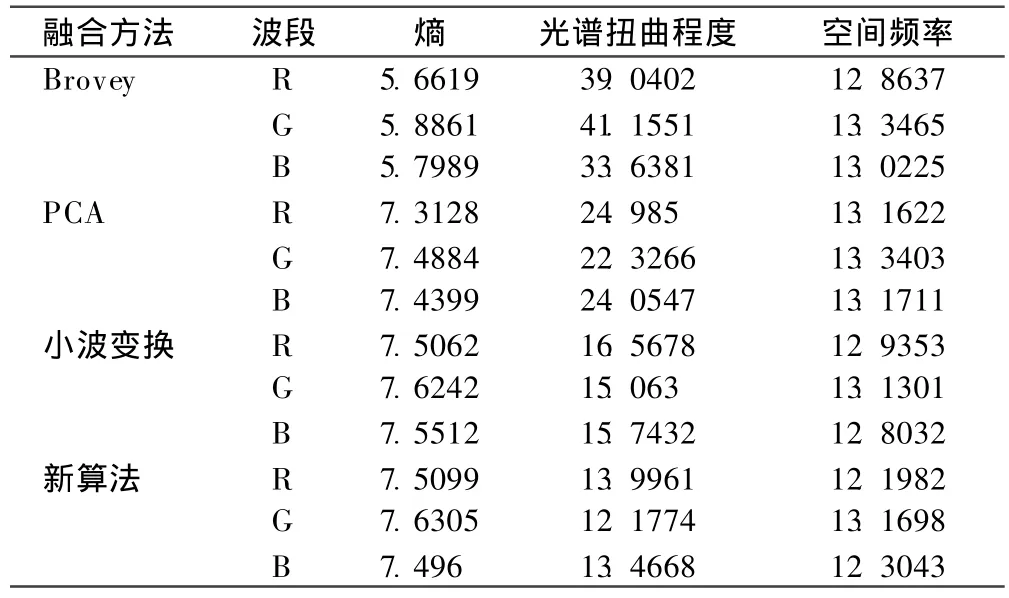
表2 多光谱数据融合客观评价
5 结 语
笔者提出了一种基于曲波变换的遥感图像融合新算法,并与Brovey变换、PCA变换和小波变换等融合算法进行了比较。结果表明,新算法在光谱信息保持方面效果较好,但在融合规则上还有待进一步改进,以期取得更优的融合效果。
[1]Goshtasby A A,Nikolov S.Image fusion:Advances in the state of the art[J].Information Fusion,2007,8(2):114~118.
[2]Pohl C,Genderen J L.Multisenso r image fusion in remote sensing:concepts,methods and applications[J].International Journal of Remote Sensing,1998,9(5):823~854.
[3]Candè s E J.Ridgelet:theo ry and applications[D].Stanford:Department of Statistics,Stanford University,1998.
[4]Candès E J,Donoho D L.New tight frames of curvelet s and optimal representations of objects with piecewise-C2 singularities[J].Comm.on Pure and Appl,2004,57:219~266.
[5]Candè s E J,Donoho D L,Yin G L.Fast discrete curvelet transforms[R].California:Applied and Computational Mathematics,California Institute of Technology,2005.
[6]满旺.高分辨率遥感数据处理方法及铀矿地质应用研究[D].北京:中国矿业大学,2008.
[7]张强,郭宝龙.应用第二代Curvelet变换的遥感图像融合 [J].光学精密工程.2007,15(7):1130~1136.
[8]蒋年德,王耀南,毛建旭.基于2代Curvelet改进IHS变换的遥感图像融合 [J].中国图象图形学报,2008,13(12):2376~2382.
[9]许星,李映,孙瑾秋,等.基于Curvelet变换的SAR与T M图像融合研究 [J].西北工业大学学报,2008,26(3):395~398.
[10]李晖晖,郭雷,刘坤.基于Curvelet变换的SAR与可见光图像融合研究 [J].光电子.激光,2009,20(8):1110~1113.
[11]付梦印,赵诚.基于二代Curvelet变换的红外与可见光图像融合 [J].红外与毫米波学报,2009,28(4):254~258.
[12]邱宣,周则明,胡友彬.应用邻域方差加权平均的curvelet变换融合 [J].计算机工程与应用,2010,46(9):166~168.
[13]赵诚,付梦印,王立平.基于粒子群优化的多分辨率图像融合[J].兵工学报,2010,31(2):171~176.

