荷载横向分布计算方法对主梁内力的影响

徐海宾,徐 平 ,王兴国

(河南理工大学土木工程学院,河南 焦作 454003)

桥梁本身是一个三维空间结构,其精确的内力计算较为复杂。虽然目前随着计算机技术的发展,利用有限元程序建立三维模型进行桥梁结构分析已完全可以实现,但毕竟建模和计算分析过程都相当复杂,费时费力。所以在满足工程精度需要的情况下,目前在进行桥梁结构设计时,更多的还是将桥梁结构简化成平面杆系模型,利用引入荷载横向分布系数的方法完成对桥梁结构的分析计算。

1 问题的提出

对于普通的梁式桥,常用的求解荷载横向分布系数的方法有刚性横梁法(也叫偏心压力法)、修正刚性横梁法、铰接板梁法、刚接梁法以及比拟正交异性板法。由于每种方法在推导时都做了相应的简化和假定,所以每种方法都有相对应的适用条件,求解结果自然也都存在一定程度的误差。对于可以利用几种方法求解的桥梁结构,用不同的方法求得的结构既然存在一定的差异性,那么究竟利用那种方法求解更好呢?下面结合一个实例加以分析。

2 实例分析

例:某装配式预应力混凝土简支梁桥,计算跨径 30m,设5道横隔梁,跨中横断面如图 1所示。

图1 横断面示意(单位:cm)

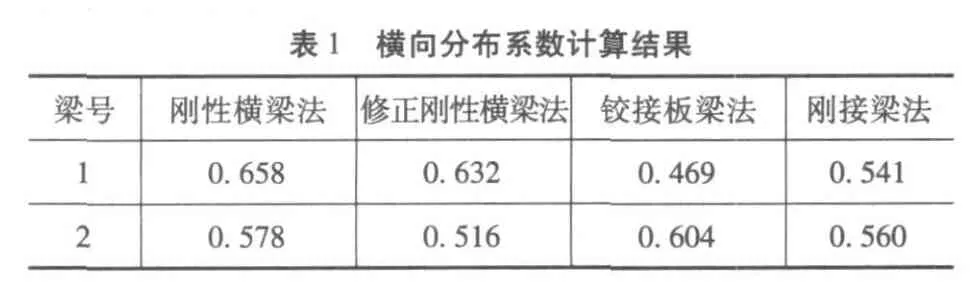
根据该桥的具体情况,求解横向分布系数时,各梁支点处利用杠杆原理法求解,跨中处可利用(修正)刚性横梁法、铰接板梁法、刚接梁法以及比拟正交异性板法中的任何一种求解。表1为利用不同方法求得结果的对比。

?

?

在表1计算时,近似取修正系数 β=0.9。另外考虑到比拟正交异性板法需要查阅大量的图表,目前亦不常用,故没有利用该方法进行计算。

对表1中数据,若以刚性横梁法为基准,利用各种方法求得的数据比值为 1号梁:1∶0.96∶0.71∶0.82;2号梁:1∶0.89∶1.04∶0.97;3号梁:1∶1∶1.5∶1.3。由表中数据及比值分析可见,各方法所计算结果存在差异,且有的相差比较大。若从偏于安全及施工方便考虑,多取各梁中最大的横向分布系数作为所有梁的横向分布系数采用,则各种方法所计算最大值的比值为 0.658∶0.632∶0.621∶0.560=1∶0.96∶0.94∶0.85。结果差异在 15%以内。

根据主梁活载内力计算公式

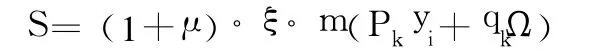
可知,所计算的活载内力差值也控制在 15%以内。而根据大量的工程实例计算表明,对于公路桥,汽车及人群荷载在总荷载中的比重在跨径较小时占40%左右;随着跨径的增大,其所占比例逐渐减小,甚至只有10%左右;若考虑超静定结构中温度力、预加力次内力及基础变位等等作用力后,活载所占比重将进一步减小。

3 结 论

由以上分析可知,采用不同方法计算荷载横向分布系数,结果之间存在一定程度的差异,有的差异甚至较大。若考虑到设计时多取最大值以及在公路桥梁中活载所占总荷载的比重较小,则差异是可以忽略的,均可满足工程需要。所以在计算荷载横向分布系数时,只要适用条件满足要求,则无论用何种方法计算,结果都是可以接受的。当然,若需要知道主梁的精确受力,最好还是建立桥梁结构的三维空间模型,利用有限元程序进行精确分析。

[1]范立础.桥梁工程(上)[M].北京:人民交通出版社,2001

[2]JTGD 60-2004公路桥涵设计通用规范[S]