用单纯形法求解确定型投标决策问题

谢小波,王月明,张井泉,邹 宇

(1.西南科技大学土木工程与建筑学院,四川 绵阳 621010;2.核工业西南勘察设计研究院有限公司,四川 成都 610061;3.四川建兴工程造价咨询有限公司,四川 成都 610100)

众所周知,建设工程招标投标伴随着一定的风险。工程承包单位要想在投标竞争中既能顺利中标又能获得可观利润,仅靠使用招投标的基本方法远远不够,还必须高度重视招投标优化方法的应用,必须研究投标决策。

1 决策成立的必备条件

决策是为实现某一目标,运用科学的理论与方法,系统的分析主观条件,提出各种方案,从中选择出一个能最佳实现目标的最优方案,以达到最佳的经济效果和社会效果的过程。因此一个决策问题的成立,必须具备下列的条件:

(1)有明确的目标(包括总目标和分目标)。

(2)存在两个以上为实现同一目标可相互替代的策略或方案。

(3)在不同的自然情况下,各策略的实施结果可依据一定的理论与方法估计出来。

(4)在各种策略中只能确定一个行动方案。

所谓确定型决策指的是决策者对决策目标的未来发展有十分清楚的了解,其有关条件都能准确的实例,每种决策只可能有一种后果。确定型决策除必须具备决策问题的 4个必备条件外,它还应该有一个特定的条件,即决策对象所处的自然状态是确定的。确定型决策的关键在于人们如何正确估计自然状态,在实践中人们往往由于无法了解唯一存在着的自然状态而使决策失误。因此从某种意义上说,确定型决策的成败很大程度上依赖于预测的准确性。本文介绍一种线性规划决策方法来定量评价投标备选项目,为承包商做出正确投标决策提供理论依据。

2 线性规划决策法的基本原理和求解步骤[1]～[8]

线性规划的理论和方法广泛地应用于军事、经济、工业、农业等各行业的计划安排、组织管理等方向的决策分析。线性规划是模型选优决策的一种具体方法。其基本思路就是在一组线性等式和不等式约束下求解线性函数的极值问题,最后再结合投标企业的情况综合考虑后做出投标决策。

2.1 线性规划模型的建立

如何合理地利用有限的资源取得最好的经济效果,是施工企业管理中经常出现的问题。线性规划是线性确定性条件下解决此类问题的有效方法,线性规划模型的建立即是将实际的决策问题抽象转化为数学模型来处理。

数学模型中的决策变量为具体投标备选项目的投标个数,用 x1,x2,x3…表示。

建立线性规划的数学模型:

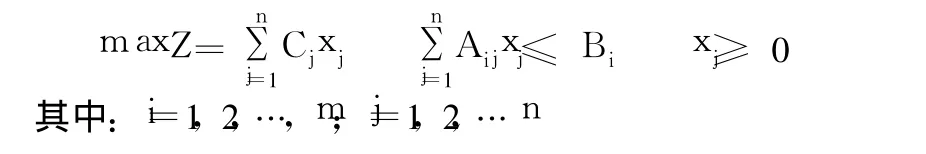
2.2 线性规划问题的单纯形解法

建立实际决策问题的线性规划模型后,接下来的问题就是求解线性规划问题了。一般求解线性规划问题的最常用的方法有两种:图解法和单纯形法。当线性规划问题只包括两个变量的时候一般使用图解法;如果需要求解多个变量的线性规划问题,则需要使用单纯形法求解。

单纯形法是求解线性规划问题的基本方法之一,其基本思路是根据问题的标准,从可行域中某个基本可行解(一个顶点)开始,转换到另一个基本可行解(顶点),并且使函数达到最大值时,问题就得到了最优解。用单纯形法的求解过程比较麻烦,但可用单纯形表来求解。所谓单纯形表是把用单纯形法求出的基本可行解、检验其最优险、迭代步骤都用表格的方式计算求出。其表格的形式有些像增广矩阵,而其计算的方法也大致使用矩阵的行的初等变换。

2.2.1 求初始解

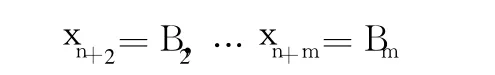
为初始基可行解,其中取正值的变量称为“基变量”,取“0”值的变量称为“非基变量”,故有m个基变量和 n个非基变量。将这些内容记入初始单纯形表(表 1)。

?

表中 XB列中填入基变量;CB列中填入基变量价值系数;Bi列中填入约束方程组右端的常数;Cj行中填入所有基变量、非基变量的价值系数;θi列的数字是在确定换人变量后,按 θ=m in(Bi/Aij),规则计算后填入;最后一行称为检验数行,对应各非基变量xj的检验数为:

表1为初始单纯形表,每迭代一步构造一个新的单纯形表。

2.2.2 寻求最优解

由于初始基可行解中所取的基变量是 xn+1,xn+2,…,xn+m,它们在目标函数式中的系数均为 0,故初始单纯形表中的Cj-Zj就分别与表中最上方xj在目标函数式中的系数Cj相同。若在上述表中所有的Cj-Zj≤0,即所有的判定数值都是零或负数,则说明初始解即为最优解。表 1中:C1,C2,…,Cn,Cn+1,……,Cn+m为目标函数式中各变量的系数。

3 线性规划决策法投标决策案例应用

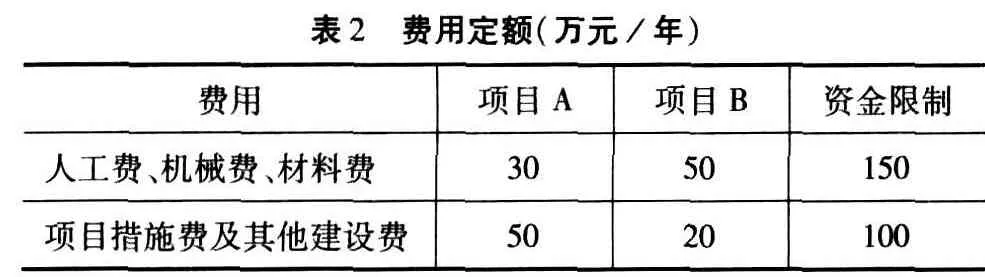
下面以某承包商要在同一时间内对两个不同的项目进行投资决策的例子来说明如何求解此类问题。某建设工程承包公司准备同时承包两个项目A和B,但是现在要求其每年消耗的总人工费、机械费和材料费不超过 150万元,总耗项目措施费及其他建设费不超过 100万元,两个项目每年分别的消耗费用见表 2。如若项目 A每年能获得利润 200万元,项目B每年能获得利润 100万元。请问两个项目的工期各自控制在多久,可以使该承包商在充分利用有限资金的条件下获利最多?

?

3.1 确定决策变量,建立线性规划的数学模型

先设变量:x1为项目 A的工期;x2为项目B的工期;x3,x4为对两个不等式约束引入的非负松弛变量。再写出其约束条件:

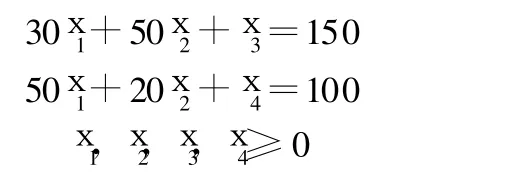
最后写出目标函数:Zmax=200x1+100x2+0x3+0x4

3.2 用单纯形解法寻求初始解

该标准型系数矩阵中已有现成的单位矩阵,既由 x3,x4对应的系数列向量构成,于是可以直接建立初始单纯形表,见表 3所示。

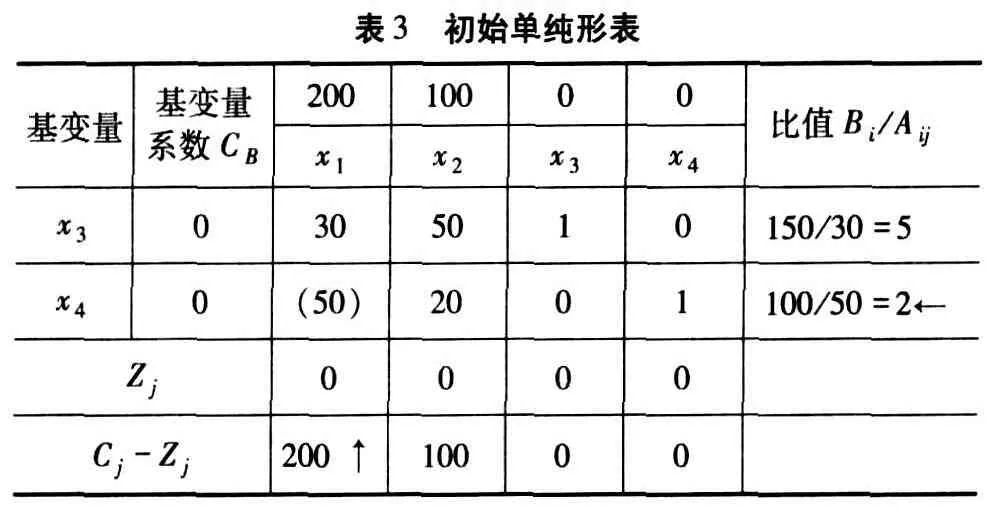
注:①选择 x3,x4作为基变量;②选 应的变量 x1进基;③选对应的基变量x4出基;④表中的“←”表示该列为主元列,“→”表示该行为主元行,“()”表示该括号中的数字为该表的主元素。

3.3 用单纯形解法寻求最优解

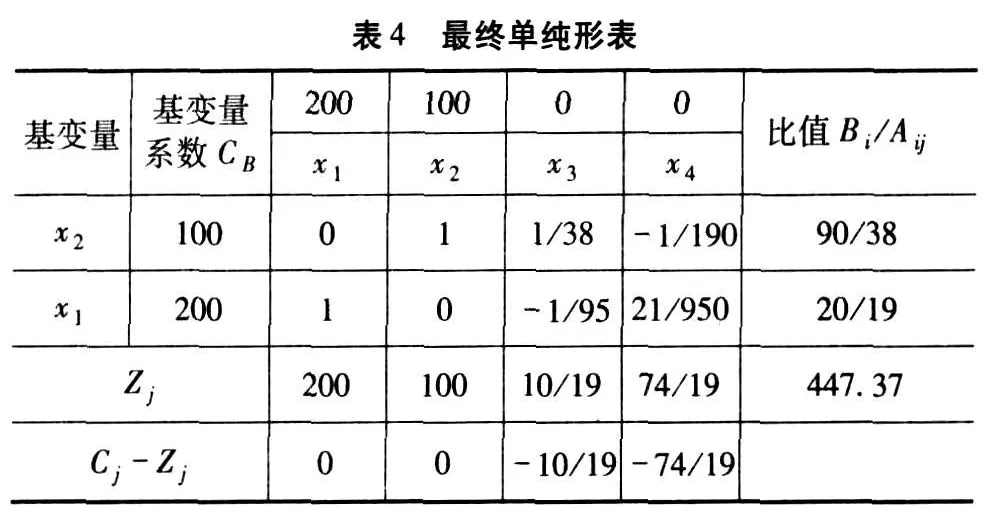
注:所有的检验数 Cj-Zj均为非正值,即说明该表已经成为最优表。

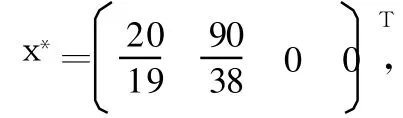
4 结束语

虽然决策结果要求被选策略必须最优,但是由于决策对象总是在多种约束条件下存在的,而人们对影响事物发展变化的因素的认识又很有限,并且是在不断的深化与发展,因此,所谓的“最优策略”也是相对的, 有条件的。当人们的认识深化了,对“最优”的结果也可能随之而变化;当约束条件变化了,策略的优劣性也会发生变化,从而使决策结果也随之而变。

就以上面的线性规划问题来说,这里的最优决策也只是针对在消耗费用的条件下,为了获得最高利润而优化的工期。其实在实际情况下决定工期根本由不得施工单位自己,更不可能仅仅通过所用费用来决定施工工期;工期的决定因素很多,包括施工项目的工程量大小、施工项目的规模、业主对各方面要求的综合、天气的变化情况以及施工的地质条件等等。所以,本文讨论的这种求工期的优化决策方法的实用性不强,只是理论探讨,只能作为求施工工期时的一个可以考虑的方面而已,也就是说,对投标决策的研究还需进一步深化。

[1]李相国.建设项目投标报价决策与风险分析[M].北京:中国水利水电出版社,2007

[2]吕炜.工程量清单投标报价模型与投标报价策略研究[D].重庆大学,2006

[3]管军,李文华.建设项目投标报价风险决策方法研究[J].技术经济与管理研究,2000(4):39-40

[4]卢德林,张祥荪,马桂芝.土建工程报价优化模型[J].系统工程理论与实践,2002,22(9):47-53

[5]陈建森.工程投标决策模型分析初探[J].南京建筑工程学院学报,2002(4)

[6]鲁耀斌,黎志成,石双元.招标投标过程中最优投标策略研究[J].华中理工大学学报,1997,25(11):6-8

[7]姚传勤.线性规划决策法在建设工程投标决策中的应用[J].建筑经济,2006(8):61-62

[8]钱颂迪.运筹学(修订版)[M].北京:清华大学出版社,1992:297-299