基于 ANSYS的悬臂浇筑拱桥最大悬臂状态索力优化

张大伟,谢尚英

(西南交通大学,四川 成都 610031)

钢筋混凝土拱桥悬臂浇筑施工法利用临时斜拉索扣住已浇筑好的拱圈节段,采用移动挂篮从拱脚开始对称逐段悬臂浇筑拱圈混凝土,直至拱顶合龙。采用斜拉扣挂法施工中的扣索索力对施工过程中拱圈内力、成桥后拱圈内力与线形有一定影响,因此寻找一组合理的施工扣索索力是十分必要的,也是目前国内外研究的重点之一。近几年有学者将最优化理论引入到拱桥悬臂施工扣索索力计算中,并取得了较好的成果,如文献[1]。本文基于ANSYS优化设计功能,将最优化方法(一阶方法)用于最大悬臂状态索力调整计算,通过设置目标函数,约束设计变量和状态变量,迭代优化出最佳索力,确保调索阶段施工安全并达到理想成桥状态。

1 最优化计算方法(一阶方法)

1.1 数学模型

设有约束多变量最优化问题为:

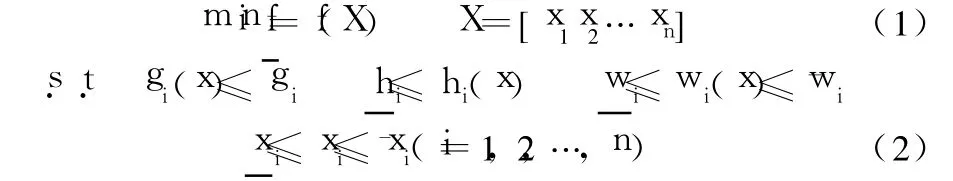
式中:f为目标函数;X为设计变量;gi、hi、wi为状态变量,它们都是设计变量的函数。

使用一阶分析法将有约束问题通过添加罚函数转化为无约束问题。转化后的无约束目标函数形式如下:

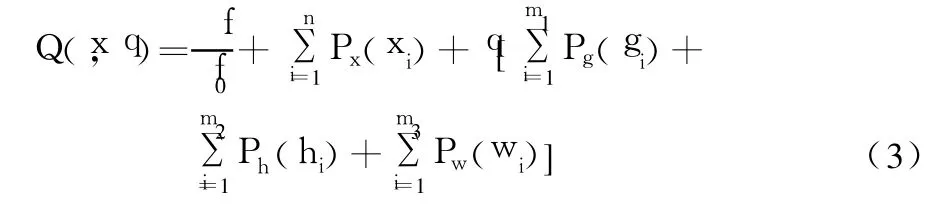
式中:Q为无单位的无约束目标函数;Px、Pg、Ph、Pw为设计变量与状态变量的罚函数;f0为参考目标函数值;q为控制约束的函数,它决定了约束函数的满意程度。

1.2 搜索方向

若迭代结果 xj未满足收敛条件,下一次迭代步长和搜索方向由式(5)确定。

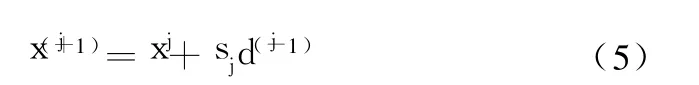
式中:sj为搜索步长,采用黄金分割法和二次插值结合的方法求得。搜索第一步按负梯度方向,以后由共轭梯度法确定。

1.3 收敛条件

对于一阶分析法,当循环满足以下任一条件时,程序将终止计算。

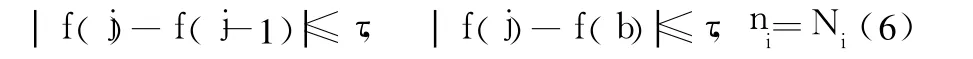
式中:f(b)为当前最优的函数值;ni、Ni分别为迭代次数和用户指定的最多迭代次数。

2 工程算例

2.1 工程及模型简介

已建的西攀高速公路的白沙沟 1号大桥,属箱型钢筋混凝土拱桥。采用挂篮悬臂浇筑施工工艺成拱,在国内尚属首次。主拱净跨 150m,拱轴线采用悬链线,净矢高 30m,矢跨比 1/5,拱轴系数 1.988,主拱材料为C 50混凝土,扣索材料为j15.24钢绞线。半孔结构及扣挂系统如图 1所示,有限元计算模型如图 2所示。

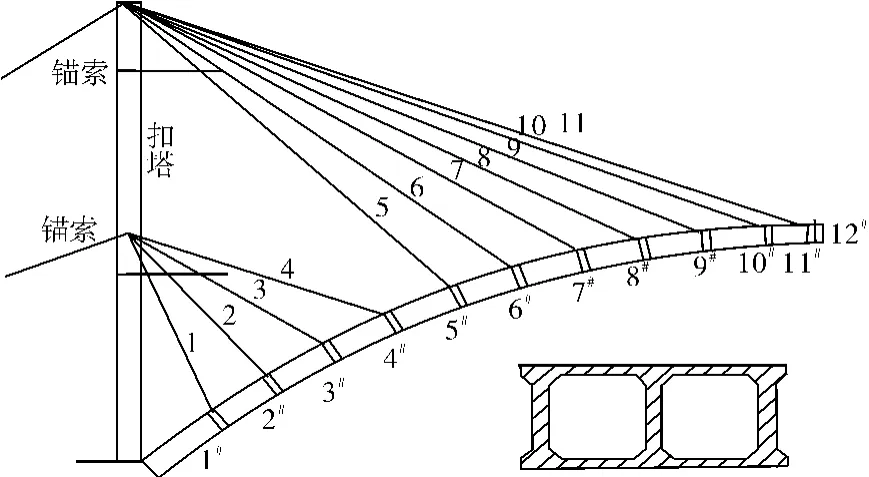
图1 主拱及扣挂系统立面

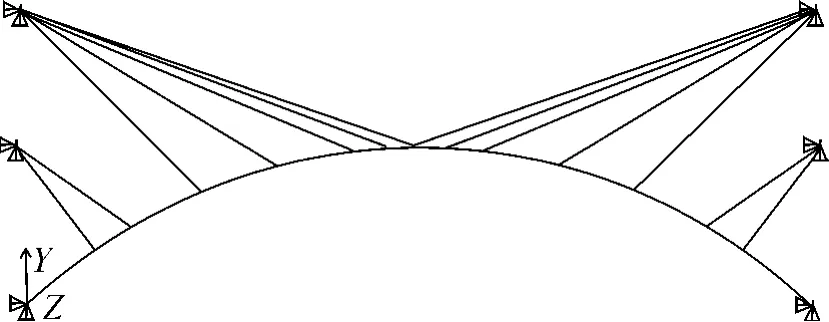
图2 有限元计算模型

最大悬臂状态索力调整是为了成桥后逼近理想成桥状态。本次计算的初始状态为最大悬臂状态,索力调整从拱脚至拱顶依次调整一次,最终状态为恒活载加载。悬臂浇筑阶段中扣索力同样可以利用一阶分析法优化计算,属于另外一个优化问题,本文只利用其结果中最后一个阶段索力作为最大悬臂索力。ANSYS中具体施工阶段划分见表 1。

?

2.2 优化变量的选取

本次优化计算的目的是通过合龙前调整扣索力,使得运营阶段拱圈压力线偏心距最小,从而使拱圈接近最佳受力状态。因此目标函数可以取运营阶段各截面偏心距平方和均值的平方根。将索力调整量转化为等效温度载荷,并以此温度载荷为设计变量。选取各调索阶段过程中的最大索力、截面最大拉应力及运营阶段截面最大拉压应力为状态变量。扣索力满足施工要求的安全系数,且不能受压,截面最大拉应力限制在 1.5MPa内。在运营阶段,最大拉压应力限值参考《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTJ 023-85)。

2.3 计算结果

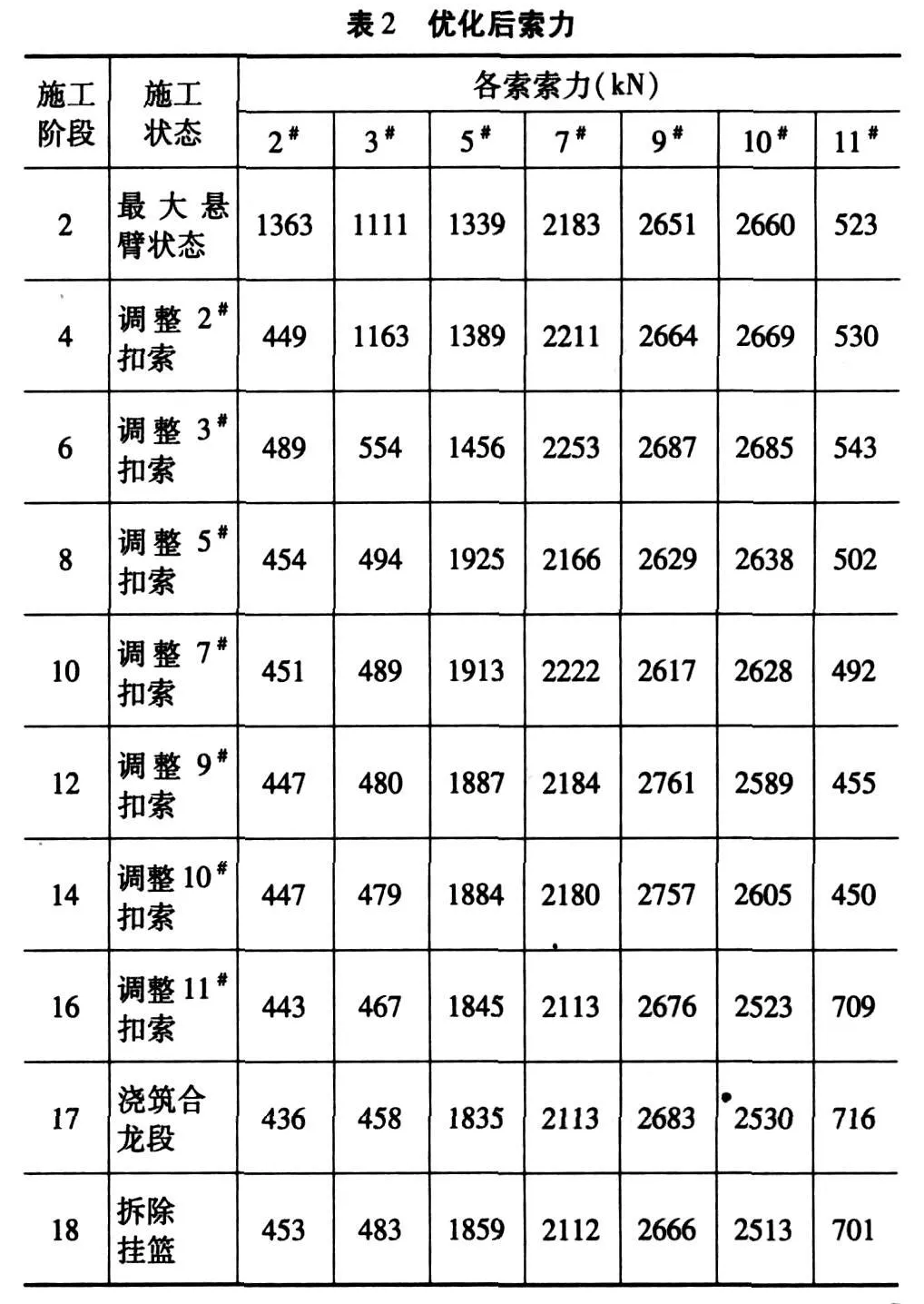
一阶分析法优化过程包含多次优化迭代,每次优化迭代又包括多次子迭代,这些是为了确定下次搜索方向和搜索步长,每次子迭代则包含一个完整施工过程的计算。目标函数反应的各运营阶段压力作用点的偏心,从优化前的 2.026m降低为优化后的 0.592m,可见优化效果明显。迭代步骤见图 3,优化后索力见表 2,其余内力结果见图 4～图 6。

?

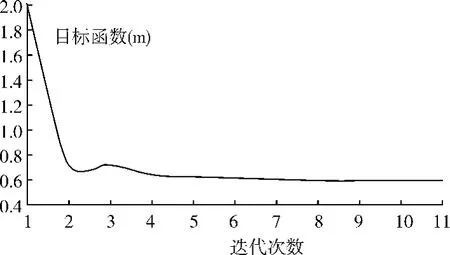
图3 目标函数与迭代次数

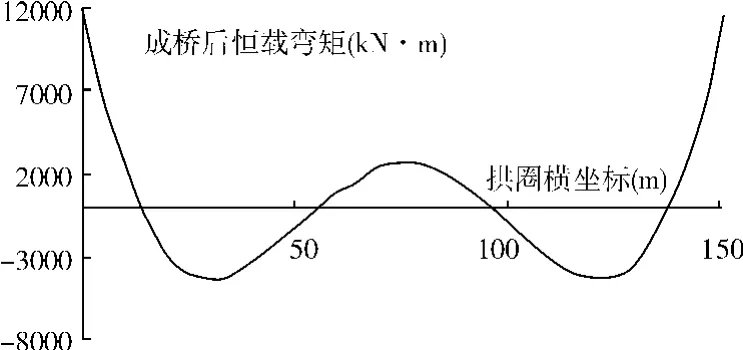
图4 成桥后恒载弯矩

图5 正常使用组合 I应力包络图

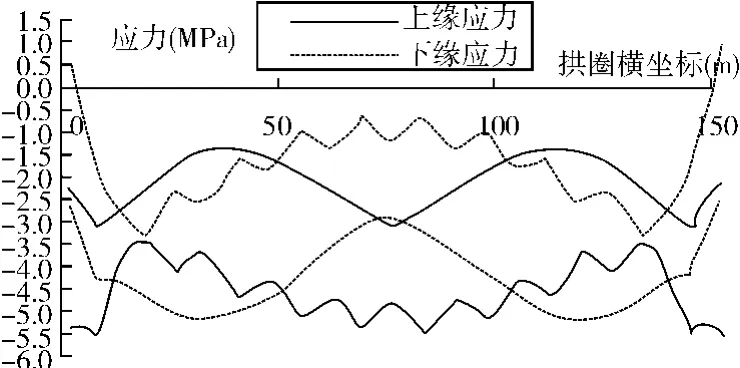
图6 正常使用组合Ⅲ应力包络图

索力表中各索力均处于较低的应力水平,保证了索力安全系数。从优化后各内力结果图中看出,成桥后使用阶段截面上下缘基本为受压状态,且压应力均满足规范要求;只有拱脚截面下缘出现拉应力,但最大值为 1.85 MPa,小于名义拉应力。可见优化效果是明显的。

3 结束语

通过对理论和实例计算表明,一阶分析法求解有约束最优问题计算精度高、收敛快;可以方便计算施工中索力,既能有效控制施工过程的截面应力和索力,确保施工安全,又能使成桥后逼近最佳受力状态。本文优化计算中没有考虑主拱的线形,是因为在悬臂浇筑中可利用挂篮调整节段预抬高。本文不足之处在于没有考虑混凝土收缩徐变影响,计入拉索非线性时做了简化。如果考虑混凝土收缩徐变影响并且利用迭代准确计入拉索非线性,此法可以应用于大跨斜拉桥施工阶段或成桥合理索力计算,具有很强的应用前景。

[1]张建民,郑皆连.大跨度钢管混凝土拱桥吊装过程的优化计算方法[J].桥梁建设,2002(1)

[2]卢险峰.最优化方法应用基础[M].同济大学出版社,2003

[3]ANSYS theory reference[M].USA,INC,2002

[4]龚曙光,谢桂兰.ANSYS操作命令与参数化编程[M].北京:机械工业出版社,2004

[5]JTJ023-85公路钢筋混凝土及预应力混凝土桥涵设计规范[S]