GM(1，1)残差修正模型在建筑形变预报中的应用

陈中新，蔡勇

(1.苏州工业园区测绘有限责任公司，江苏苏州 215021； 2.南通赛维测绘有限公司，江苏南通 226100)

GM(1，1)残差修正模型在建筑形变预报中的应用

陈中新1∗，蔡勇2

(1.苏州工业园区测绘有限责任公司，江苏苏州 215021； 2.南通赛维测绘有限公司，江苏南通 226100)

通过对比建筑形变监测数据的GM(1，1)模型和改进的GM(1，1)残差修正模型建模的预报结果，表明残差修正GM(1，1)模型的预报精度明显高于传统GM(1，1)模型的预报精度，并且二次残差修正GM(1，1)模型的预报精度远高于一次残差修正GM(1，1)模型的预报精度，从而为准确形变预报提供了一种简单而有效的新实践。

GM(1，1)模型；残差模型；形变预报

1 前 言

目前，城市的高层及超高层建筑越来越多，其结构体型、施工工艺也日益复杂，施工过程中常常受到基础周围土质的变化(如松动、水层侵蚀等地质条件的影响)以及上部荷载的作用，造成基础变形；在运营过程中也会因为风流和温度变化使建筑物产生形变，轻者出现裂缝，重者危及安全，因此变形监测和形变预报已成了运营管理、安全使用的重要指导，受到了全社会的普遍关注。

常用的建筑物形变预报有回归分析[1]、最小二乘配置法[2]等方法，在实际工程应用中，由于观测条件等客观因素的噪声影响，难于满足分析方法要求的观测数据为大样本，具有特征分布的要求，而GM(1，1)模型灰色预测[3]属于非线性外推预测，具有所需样本数据少，建模简单等优点，因此得到了广泛的应用，但其预报有时特别成功，有时却精度不高，从而引发了许多研究者从模型的初始值的选取[4]、背景值的构造[5～6]等方面进行深入的研究，力图找出影响GM(1，1)模型精度的关键因素。本文引入GM(1，1)的残差修正[7]对原始模型进行改进，并通过建筑形变预报实例验证表明，残差修正模型的预测误差明显缩小，精度明显高于传统GM(1，1)模型。

2 GM(1，1)模型和GM(1，1)残差修正模型

2.1 GM(1，1)模型建模过程

设已知参考数据列为x(0)＝[x(0)(1)，x(0)(2)，…，x(0)(n)]，做1次累加生成数列:

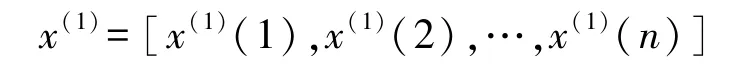
均值数列:

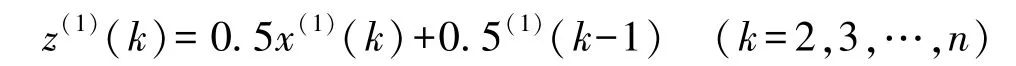
于是建立灰微分方程为:

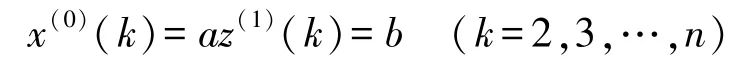
相应的白化微分方程为:

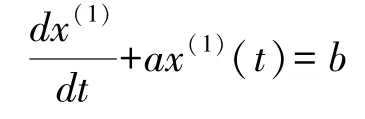
根据最小二乘原理，GM(1，1)模型中的参数向量为:

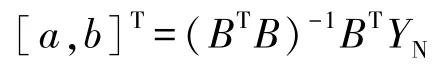
代入白化微分方程，得:

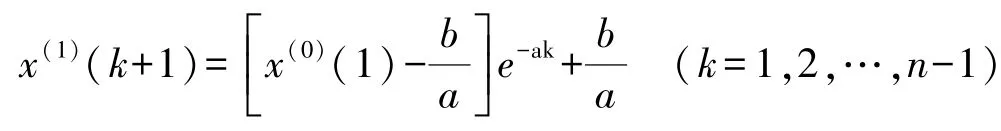
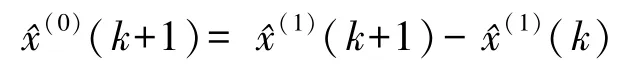
2.2 GM(1，1)残差修正模型

从而利用残差模型对原模型进行修正得到:

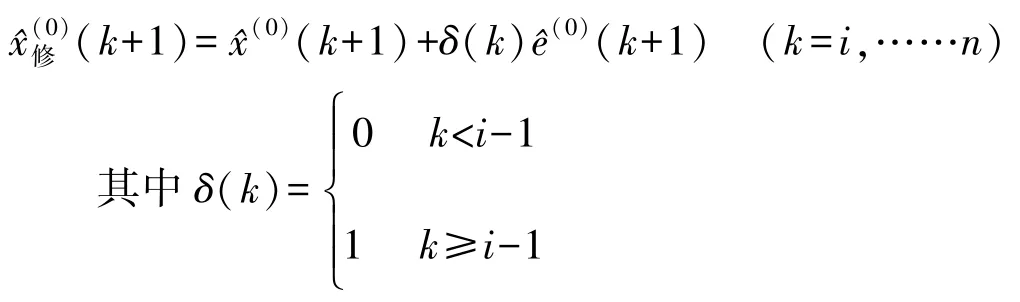
3 应用分析

武汉市某居民小区发生地陷事故，为实时了解建筑物的安全情况，对该小区居民楼进行了定期的监测。取X－4号点的沉降观测数据[8]进行GM(1，1)残差修正模型的建模分析。数据如表1所示。

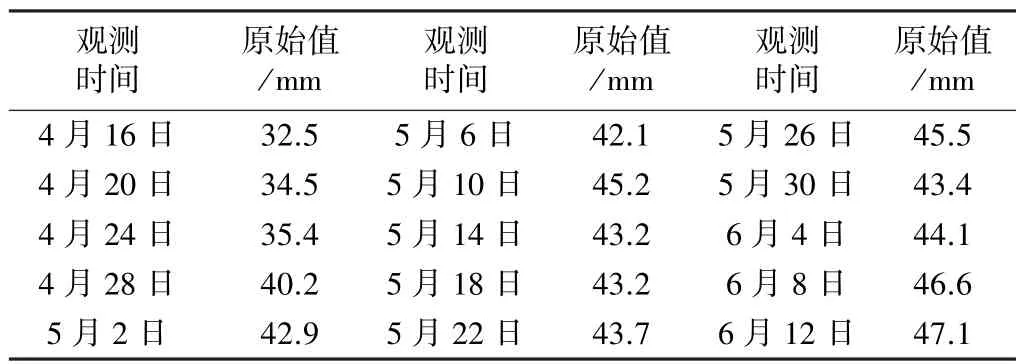
武汉某居民楼X－4号点监测数据[8] 表1

首先对上述15期观测数据，建立15维的GM(1，1)原始预测模型，在Matlab软件中编程计算，其模拟的结果如表2所示。

然后对GM(1，1)原始模型计算得到的残差序列进行正化处理，并剔除第一期的残差，把剩余的14期残差建立修正模型，再把残差的残差建立修正模型，其模拟结果如表3所示。

为了检验GM(1，1)原始模型和二次残差修正模型的预测精度，分别用上述建好的15维GM(1，1)原始预测模型和二次GM(1，1)残差修正模型对6月16日和6月20日的未来二期形变量进行预测，结果分析如表4所示。

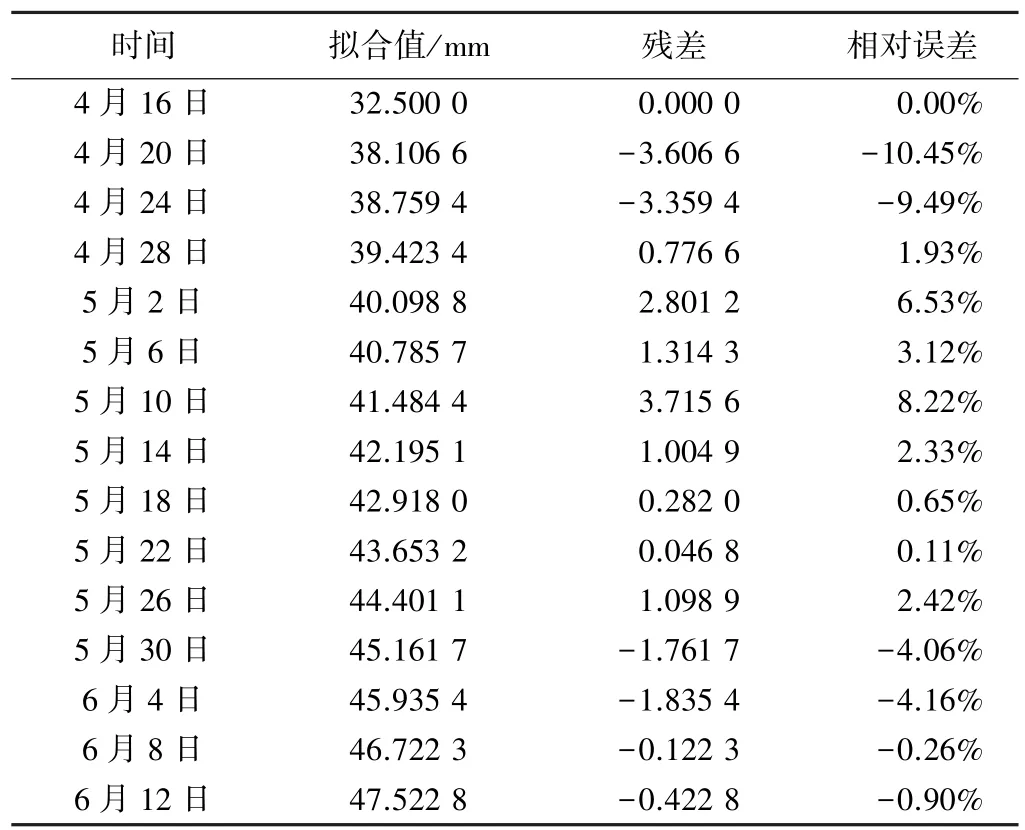
GM(1，1)原始模型计算结果 表2

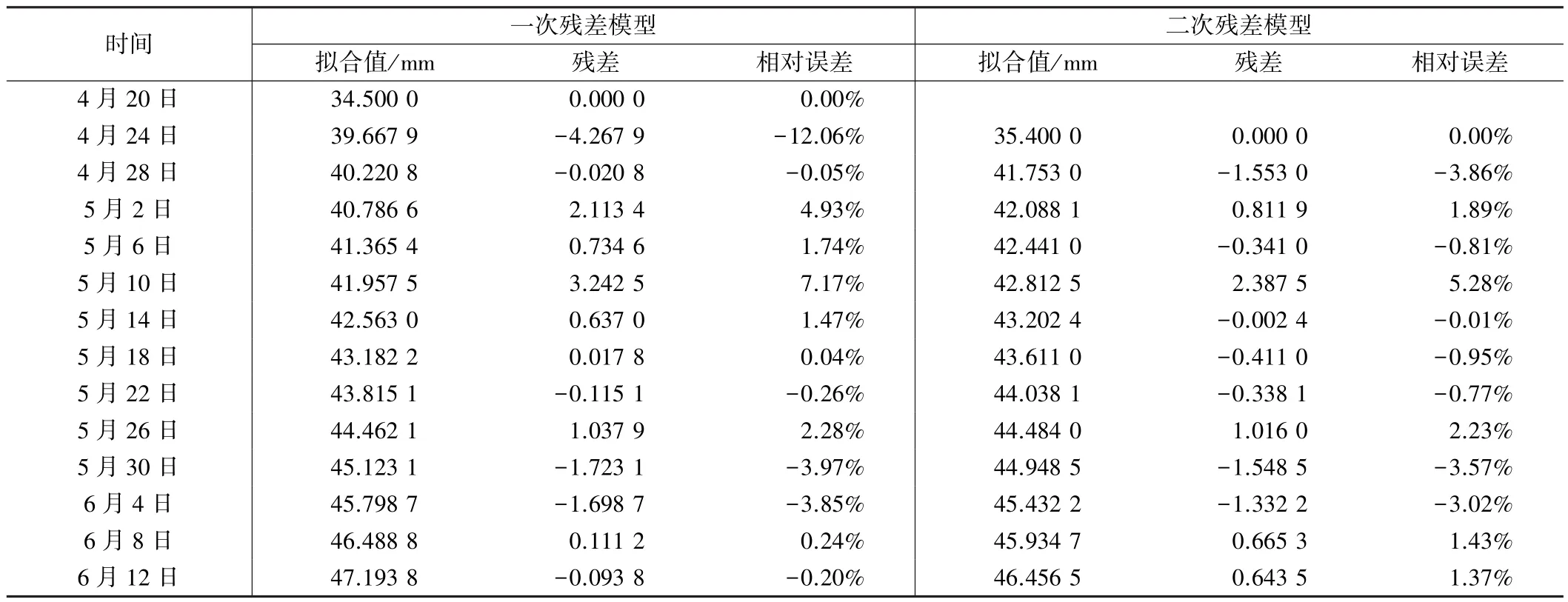
GM(1，1)残差修正模型计算结果 表3

两种模型的预测结果分析 表4

4 结 论

GM(1，1)模型经过残差修正后，预测精度均有不同程度提高。通过对建筑物监测实例计算分析，结果表明:

(1)经过残差修正的GM(1，1)模型的精度有所提高。其二次残差修正GM(1，1)模型的精度远高于一次残差修正GM(1，1)模型，可以应用于建筑物的形变预报。

(2)形变的随机扰动或驱动因素比较复杂，因此建模预报精度仅限于较短的时期，所以实际应用中应采用最新的观测数据建模进行预测。

(3)用残差进行修正时，残差段的选取对模型预测的最终精度有很大的影响，应综合考虑项目具体荷载变化、观测周期等影响因素选择合适的残差尾段进行建模，从而达到提高模型精度的效果。

[1]陈伟清.回归分析在建筑物沉降变形分析中的应用[J].测绘学院学报，2005(4):249～251

[2]魏玉明，党星海.最小二乘配置法在建筑物形变监测分析中的应用[J].城市勘测，2008(3):133～135

[3]邓聚龙.灰色系统基本方法[M].武汉:华中理工学院出版社，1981

[4]张辉，胡适耕.GM(1，1)模型的边值分析[J].华中科技大学学报:自然科学版，2001，29(4):110～111

[5]谭冠军.GM(1，1)模型的背景值构造方法和应用[J].系统工程理论与实践，2000，20(4):98～103

[6]罗党，刘思峰，党耀国.灰色模型GM(1，1)优化[J].中国工程科学，2003，5(8):50～53

[7]张艳芳.基于GM(1，1)的残差修正模型及应用[J].水科学与工程技术，2005(6):51～53

[8]方毅，花向红，李海英等.灰色神经网络模型在建筑物变形预报中的应用[J].测绘工程，2008(2):51～53

Gm(1，1)Residual Error Correction Model Applied to Building Deformation Prediction

Chen ZhongXin1，Cai Yong2
(1.Suzhou industrial park survey and map department，Suzhou 215021，China；2.Nantong Saiwei survey Co.，Ltd.Nantong 226100，China)

This deformation monitoring data by comparing the construction of the GM(1，1)model and the improved GM(1，1)residuals revised forecast modeling results，indicating that residual modification GM(1，1)model forecast accuracy significantly higher traditional GM(1，1)model forecast accuracy，and the second amendment to the residual GM (1，1)model prediction accuracy is much higher than a revised residual GM(1，1)model forecast accuracy，so as to accurately deformation prediction provides a simple and effective new practice.

GM(1，1)model；remaining model；deformation prediction

1672－8262(2010)03－133－03

TU196

B

2009—09—26

陈中新(1974—)，男，高级工程师，主要从事城市测绘以及工程测量数据的分析、处理。