实时动态灰色模型及其变形监测应用

程晓晖，侯凯，罗涛

(1.广州市城市规划勘测设计研究院，广东广州 510060； 2.郑州市规划勘测设计研究院，河南 郑州 450052；3.中科院高能物理研究所，北京 100049)

实时动态灰色模型及其变形监测应用

程晓晖1∗，侯凯2，罗涛3

(1.广州市城市规划勘测设计研究院，广东广州 510060； 2.郑州市规划勘测设计研究院，河南 郑州 450052；3.中科院高能物理研究所，北京 100049)

介绍了实时动态灰色模型进行变形监测应用的效果。结果表明，与原始的灰色模型相比，该方法建立了一种新数据之间的实时关系，能够更加准确的求出满足精度要求的预测值，为变形监测的数据处理与预报提供了一种有效方法。

灰色模型；GM(1，1)；数据处理；变形监测

1 引 言

人类社会的迅猛发展，高楼大厦林立各处，一旦高层建筑发生不均匀沉降而没有被及时发现和控制，必将会造成严重的经济损失和人身安全威胁，故而对其变形监测预报已经变得越来越重要。

灰色模型是一种研究所需原始信息量少、计算简单以及预测精度较高的方法，主要通过对部分已知信息的生成，开发，提取有价值的信息，实现对系统运行行为，演化规律的正确描述和有效监控。原始的灰色模型采用最初的数据作为建立模型的依据，但数据在变化过程中，旧的数据对预测值的影响越来越小，新数据在预测中的重要性逐渐增加。而常用的GM(1，1)只是从静态的角度考虑未来时刻的状态，并未把未来可能影响系统状态的因素加入进去。因此本文对原有的GM(1，1)模型进行了改进，在选择求解时采用最新的数据，再采用动态GM(1，1)模型来进行求解，这样预测所得到的数据与真实数据之间产生了更大的联系。通过对实测数据分析可以看出，文中所提出的基于实时动态灰色模型可以作为预测的一种新方法，且预测精度比原始GM(1，1)要好。

2 灰色模型GM(1，1)的建立

记原始数列为:x(0)＝{x(0)(1)，x(0)(2)，…，x(0)(k)}，k为序列长度。对x(0)进行一次累加生成处理(1－AGO)，得到生成的数列x(1)＝{x(1)(1)，x(1)(2)，…，x(1)(k)}，对此生成序列建立一阶微分方程

记为GM(1，1)。a，u为待识别参数即灰参数，其白化值(灰区间中的一个可能值)为y≫＝[a，u]T，用最小二乘法求解，相应的公式为:

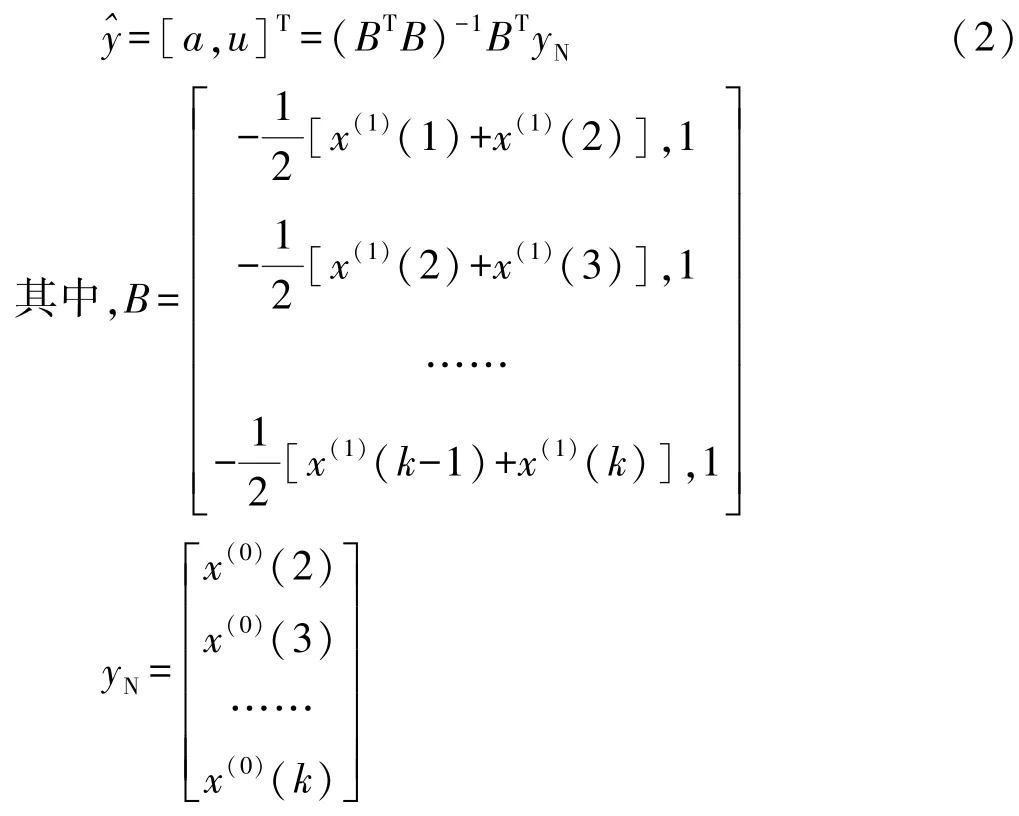
解出微分方程得到其离散的通解为:

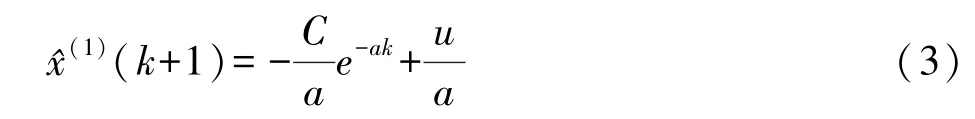
其中，C为积分常数。

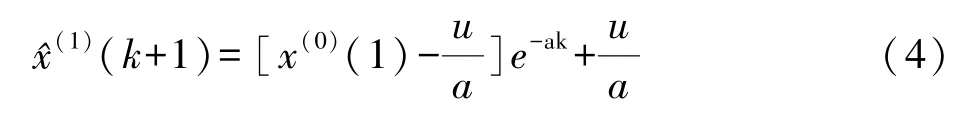
从而可以求得预测公式为:

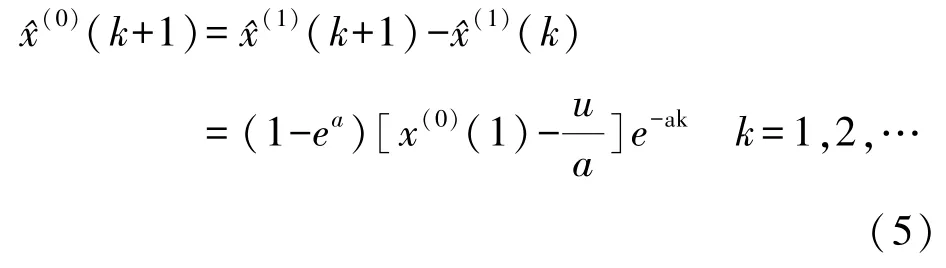
3 精度评定

灰色GM(1，1)模型的精度一般用后验差方法来检验。它由后验差比值C和小误差概率P共同描述。计算残差数列e，相对误差q:

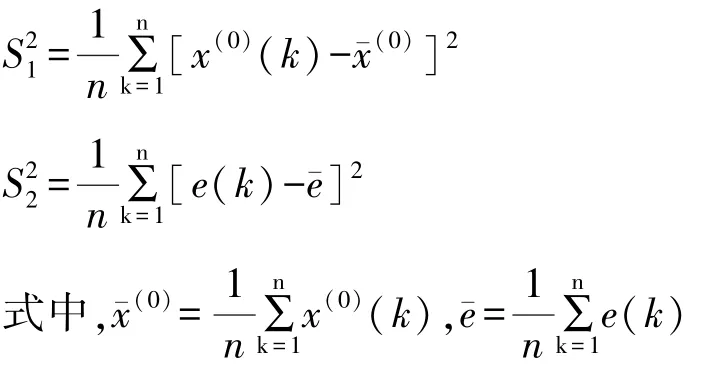
然后计算后验差比值C＝S2/S1和小误差概率p＝{｜e(k)｜＜0.6745S1}。

一个好的预测模型，要求C越小越好，一般要求C＜0.35，最大不超过0.65。预测模型好坏的另一个指标是小误差概率，一般要求P〉0.95，不得小于0.7。

4 动态灰色模型

对于一个系统而言，随着时间的推移，系统受干扰的因素不断变化，系统状态也不断变化。若直接套用GM(1，1)模型进行长期预测，一方面预测精度不断降低，另一方面模型未能反映出系统的变化，其预测可信度很小。

GM(1，1)模型长期预测的有效性明显受系统时间序列长短及数据变化影响。如果系统建模选用的数据列太短，则难以建立长期的预测模型；数据列过长，系统受干扰的成分多，不稳定因素大，易使模型精度降低。为此，我们建立动态灰色模型。

设原始数列为x(0)＝ {x(0)(1)，x(0)(2)，…，x(0)(k)}进行一次AGO生成x(1)后建立GM(1，1)模型，由式(5)得到k＋1时刻预测值然后去掉x(0)(1)，加人新获得的k＋1时刻的观测数据x(0)(k＋1)，构成新的动态序列称为动态灰色模型。

5 实时动态灰色模型

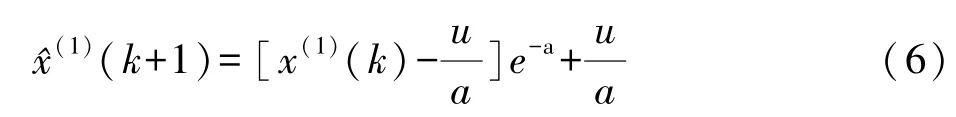
从而可以求出预测公式:

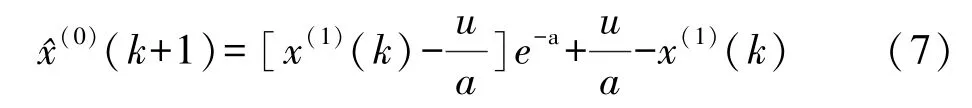
由(2)式建立动态k维实时GM(1，1)模型。设x(0)(k＋1)为最新的数据，将其代替最老的数据x(0)(1)，从而可以得到新的k维数列x(0)＝{x(0)(2)，x(0)(3)，…，x(0)(k＋1)}，按照灰色模型代入到(7)式中预测下一个，始终保持x(0)的维数为k，如此递补下去，直到所要求出的数据为止。这里的新数据可以是预测值，也可以是真值，文中所用数据可随时更新，因此新数据取真值。

6 实例分析

为了检验实时动态灰色模型进行沉降预测的效果，根据以上讨论模型，编写了Matlab程序对数据进行处理分析。采用在某超高层建筑物变形的监测中测得的某一个点的16期变形监测数据，分别应用原始GM(1，1)模型、动态GM(1，1)模型和实时动态GM (1，1)模型进行处理，得到预测值。将模型中的k设置为3，取前3个数据x(0)＝{92.83，92.39，92.21}建立模型，预测第4个数据，随后将第1个数据去掉，将第4个数据的原始值插入到初始的3个数当中，从而预测第5个数据，如此反复进行，直到求得所要预测的数据为止，三种模型预测结果结果见表1。

根据表1可以看出:

(1)原始GM(1，1)静态预测模型只能预测较短几个时间步长内的函数值，误差相对比较大，而且随时间的推移，偏差越来越大。其主要原因是在模型应用过程中灰参数是静态的、固定的，忽视了其具动态变化的特征。对一个系统来说，随时间的推移，未来的一些扰动因素将不断进入系统而对其施加影响，用之进行长期预测必然会产生较大的偏差。从结果中也可以看出，预测精度很低，而且不合格。

(2)动态GM(1，1)模型动态预测由于实时地加入了新的信息，提高了灰区间的白色度，预测效果较好，残差均在1.5 mm以内，预测精度较高。

从灰平面上看，真正具有实际意义精度较高的预测值，仅最近的一两个数据，其他远的数据仅反映一种趋势。因此，实时的加入新信息，淘汰旧信息，不仅可以突出系统最新的变化趋势，而且可以消除预测模型的噪声污染，对预测精度的提高也具有较好的作用。

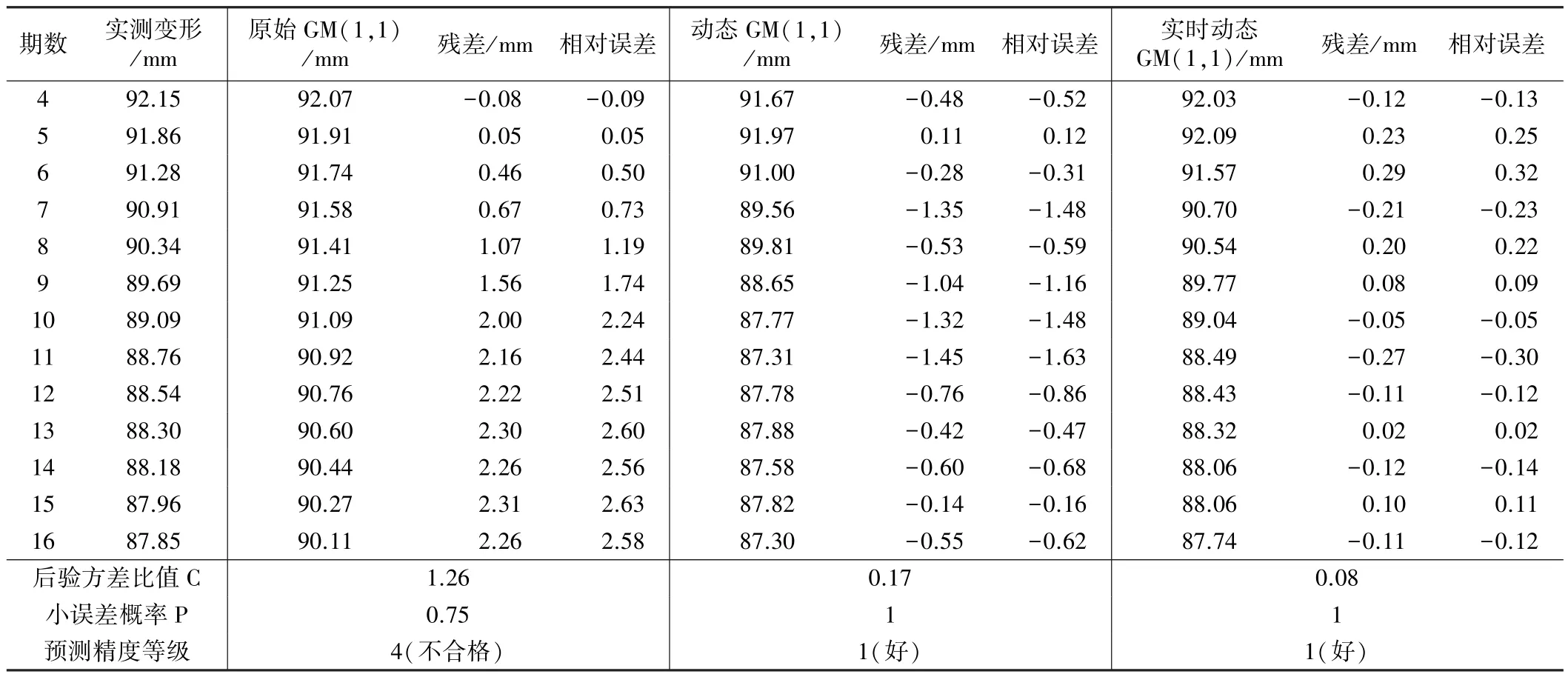
三种模型所得到的预测值 表1

动态模型弥补了原始GM(1，1)模型的不足之处，实时地引入了新的观测值或进行灰数递补，因此真实反映了系统状态的变化，可以有效地提高预报精度。

(3)实时动态模型利用少量信息即可进行预测的优势，在动态模型的基础上，又更加充分地利用了最新的信息，更倾向于新数据在预测中的重要性，其实时的动态选择过程对数据的分析预测起很重要的作用，而且精度也有较大提高。结果最好，残差均在0.3 mm以内，预测精度最高。

7 结 论

本文的实例证明，利用实时动态灰色模型进行建筑物沉降观测的成果分析，可以获得满意的沉降预测结果，为建筑物的安全评判、建筑工程的防灾减灾提供可靠的数据依据。虽然其在作长期预测时有一定的优越性，但预测时段也不能太长，其优越性是相对的。

[1]邓聚龙.灰色系统理论[M].武汉:华中工学院出社，1985

[2]黄声享，尹晖，蒋征.变形监测数据处理[M].武汉:武汉大学出版社，2003

[3]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社，1989

[4]潘华志，卫建东，夏治国等.实时灰色模型在变形预测中的应用[J].测绘科学，2007.07，32(4)

[5]刘棠洪，周俊，朱庆川.改进的灰色预测模型在地面沉降预测中的应用[J].地质灾害与环境保护，2007.09，18(3)

The Dynamic Grey Model on the Basis of Metabolism and its Application

Cheng XiaoHui1，Hou Kai2，Luo Tao3
(1.Guangzhou Urban Planning＆Design Survey Research Institute，Guangzhou 510060，China；2.Zhengzhou City Planning Survey and Design Institute，Zhengzhou 450052，China；3.Institute of High Energy Physics.The Chinese Academy of Sciences，Beijing 100049，China)

This paper mainly introduces the effect of the Dynamic Grey Model on the basis of Metabolism，which used in the Deformation Monitoring Forecasting，and the result shows that compared with the former Grey Model，this method builds some dynamic relationship between the new data，it can get more accurate data which the precision is under our satisfaction.It proves to be a useful method for the Deformation Monitoring Forecasting.

Grey Model；Metalbolism GM(1，1)；Data Analysis；Deformation Monitoring

1672－8262(2010)03－127－03

P258

B

2009—10—31

程晓晖(1984—)，男，硕士研究生，助理工程师，主要为城市测量技术工作。