斜拉桥索梁锚固结构应力分析

鄢余文

0 引言

安庆长江大桥主桥为主跨 510m的双塔双索面钢箱梁斜拉桥。钢箱梁为扁平闭口流线形,索梁锚固为钢箱式锚固结构。该结构锚箱处板件较多,连接复杂,索力较大,加上斜拉索索力对腹板会产生附加弯矩,通过理论分析和计算研究,该区域都难以准确反映其真实的应力分布情况。为此,对钢箱梁与斜拉索的锚固结构进行了静载试验,以研究锚箱附近的应变和应力状态。

1 试验模型及试验基本情况

试验模型主要包括模拟主梁、模拟索塔及张拉钢绞线三部分。模拟主梁采用了 4.75m的长度,锚箱箱体及与之连接的腹板采用了与实际结构一致的尺寸及连接方式,主梁顶、底板则加厚并向锚箱一侧延伸,采用宽 1.2m、厚 0.05m的板件。模拟索塔采用箱形钢结构构件,一方面模拟主梁的约束条件,另一方面作为加载的反力构件。张拉杆用于模拟斜拉索进行加载,加载通过安装在模拟索塔张拉架上的 900 t级千斤顶进行。

该桥的最大设计索力为 460 t,由此确定试验加载工况。进行3种工况加载:工况Ⅰ分级加载到最大设计索力;工况Ⅱ分级加载到1.7倍最大设计索力;工况Ⅲ分级加载到1.9倍最大设计索力。

2 试验结果及其分析

2.1 应力分布分析

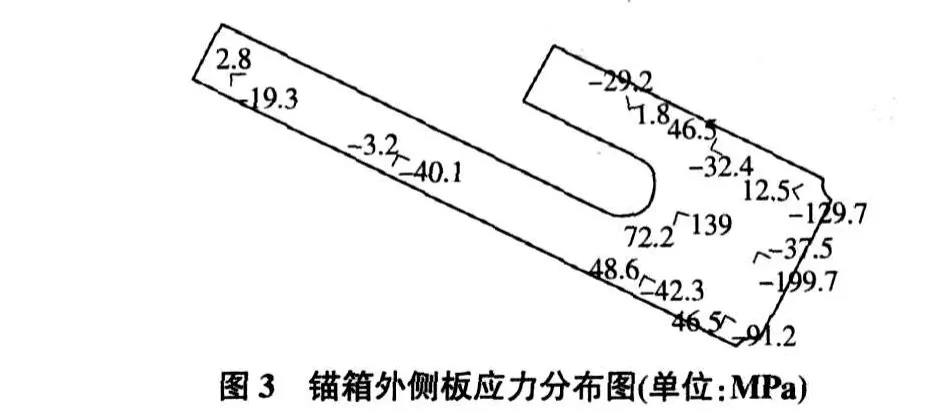
锚箱由顶板、底板、侧板、承压板、肋板构成。其中肋板不是主要受力构件,其应力较小,而承压板受力简单。此外,试验主要关心的是锚箱结构在最大设计索力 460 t下的受力情况。因此只对工况Ⅰ实际 1.0倍最大设计索力下,锚箱顶板、底板、侧板进行分析。根据试验测得的应变,可算得锚箱板件各测点的主应力及其作用方向,见图1～图 4。

从图1,图2可以看出,锚箱顶、底板均以受压为主,且受力呈现一定的规律性。主压应力方向大致平行于板边缘,即平行于张拉钢绞线方向。而在垂直于该方向,锚箱顶、底板的受力相对较小。在锚箱顶、底板靠腹板侧主压应力中间小两头大。在另一侧则相反,主压应力呈现中间大两头小的规律。在顶、底板中间,主压应力从其靠锚箱承压板端向另一端递减。由此表明,锚箱结构为偏心受压状态,使得顶、底板存在受扭现象。锚箱顶、底板在其自由端靠腹板侧应力较大,而且对于顶板,在此处另一方向还存在较大的主拉应力。

从图3,图 4可以看出,锚箱内、外侧板的两侧以受压为主,其主压应力方向大致平行于张拉钢绞线方向。而在垂直于该方向,内、外侧板的受力相对较小。锚箱内、外侧板在中间靠槽口处以受拉为主,主拉应力方向垂直于张拉钢绞线方向。而在另一端,外侧板仍以受拉为主,内侧板则以受压为主。锚箱内、外侧板的最大主压应力均发生在其靠锚箱承压板端,并由此向另一端递减。

2.2 应力发展进程分析

为了研究应力随加载的变化进程,在工况Ⅱ下,进行 14级加载。即采用分级加载从1级 0.2倍最大设计索力到 14级 1.7倍最大设计索力。取锚箱内、外侧板部分测点,根据其各级加载所得主应力,计算得各级加载等效应力,见图 5。

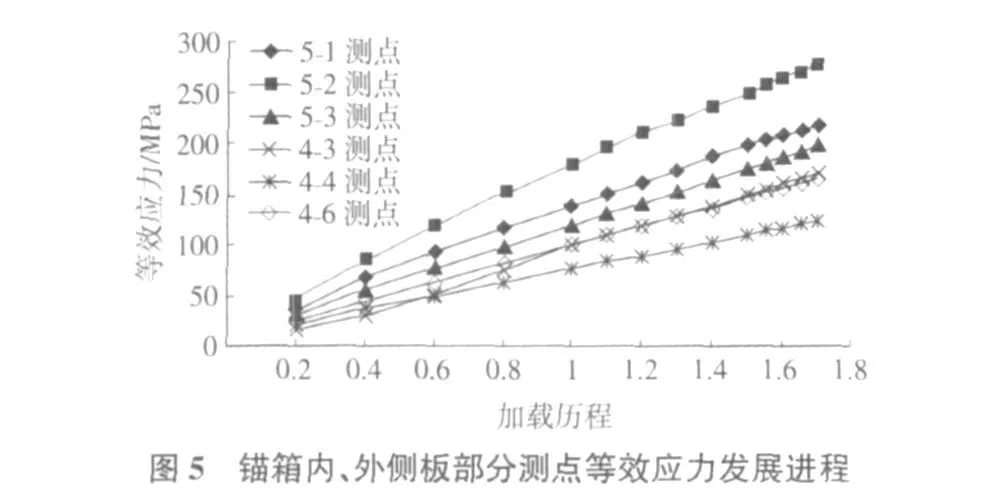
从图 5中可以看出,荷载与应力呈线性关系。表明在 1.7倍最大设计索力,即 782 t索力范围内,锚箱内、外侧板均未屈服,结构受力呈线性状态。

3 三维有限元仿真分析

本次试验模型的有限元计算,采用的是大型通用程序 ANSYS。计算模型主要采用空间板壳单元Shell43建立,在锚箱承压板和索塔上斜拉索锚固承压板处,采用了接触单元 Targe170和Conta174。由于模型中的斜拉索只是起加载作用,因此计算时采用两锚固处的等效分布荷载代替。

从图 6中可以看出,锚箱顶、底板在其自由端靠腹板侧主应力较大,且应力沿斜拉索方向逐渐减小,到达承压板附近又迅速增大,最大压应力处达到 248MPa,等效应力为224MPa。锚箱内、外侧板在其靠锚箱承压板端应力最大,且应力向自由端方向逐渐减小。锚箱以受压力为主。锚箱加劲肋板应力较小。

4 试验实测值与有限元计算值比较

根据主应力,可算得测点实测等效应力值,并把该等效应力值与有限元计算的等效应力进行比较,见表1,表2。

表1 460t索力作用下锚箱顶、底板部分测点实测应力与计算应力比较 MPa

表2 460t索力作用下锚箱内、外侧板部分测点实测应力与计算应力比较 MPa

从表1,表2等效应力实测值与计算值的比较中可以看出,大部分测点的试验实测值和有限元计算值很接近。证明试验结果符合力学规律,是可信的。同时,也证明采用三维有限元分析的索梁锚固结构应力基本能够反映实际应力分布规律。

5 结语

锚箱顶板、底板、侧板均以受压为主,主压应力方向大致平行于张拉钢绞线方向,而在垂直于该方向的受力相对较小。锚箱顶、底板最大主压应力均在靠腹板侧近主梁端,而侧板的最大主压应力值均在靠锚箱承压板端,并由此向另一端递减。在锚箱顶、底板靠腹板侧主压应力中间小两头大;在另一侧则相反,主压应力呈现中间大两头小的规律;在中间主压应力从锚箱承压板端向另一端递减。在 782 t索力范围内,锚箱结构受力呈线性状态。

有限元计算应力值与实测应力值吻合较好,证明试验结果可信,而且三维有限元方法可以用于估算实际索梁锚固结构的应力分布。

[1] 严国敏.现代斜拉桥[M].成都:西南交通大学出版社,1996.

[2] 林元培.斜拉桥[M].北京:人民交通出版社,1998.

[3] 刘庆宽,强士中,张 强,等.斜拉桥锚箱式索梁锚固区应力分析[J].桥梁建设,2001(20):66-67.

[4] 沈锐利.大跨度桥梁及城市桥梁[M].成都:西南交通大学出版社,2002.

[5] 鄢余文.安庆长江大桥索锚固结构静载与疲劳试验研究[D].成都:西南交通大学,2005.

[6] 房贞政,卓卫东,上官萍,等.三县洲斜拉桥主梁锚固区应力分析[J].福州大学学报(自然科学版),1999(18):26-28.