收缩徐变对钢管混凝土拱桥力学性能影响分析

凌海明

0 引言

钢管混凝土组合构件由于混凝土收缩徐变的作用,截面内钢管与混凝土之间存在应力重分布问题[1-3],所以对于组合截面的超静定结构,既要进行结构内力重分布分析外,还要进行截面内部的徐变应力重分布分析,系杆拱桥内部为超静定结构,由于混凝土会产生收缩徐变,而钢管不会产生收缩徐变,则在同一截面内会发生钢管与混凝土之间的应力重分布。

1 混凝土收缩徐变对结构内力的影响

现以某钢管混凝土拱桥的设计图为计算模型,按照设计的施工顺序,对该桥进行施工加载,同时计入混凝土的收缩与徐变的影响。

对于混凝土收缩徐变对结构内力的影响采用平面模型来进行计算。

在程序中对混凝土收缩量的计算是应用以下指数函数计算混凝土任一时刻t收缩量:

其中,εs(∞)为收缩应变终极值;p为收缩应变增长速率。

由于平面计算模型不能考虑横桥向各号钢管内混凝土不同时灌注的情况,在计算中作以下的处理:对上弦的四号钢管内同时灌注混凝土,且在灌注混凝土时也计入混凝土单元的刚度。

1.1 混凝土收缩徐变对结构内力的影响

为研究混凝土收缩徐变对结构的整体内力的影响,列出不计混凝土收缩徐变与计入混凝土收缩徐变,以及成桥初期与1年～4年后等时期的各控制截面的全截面轴力与全截面弯矩,如表1,表2所示。

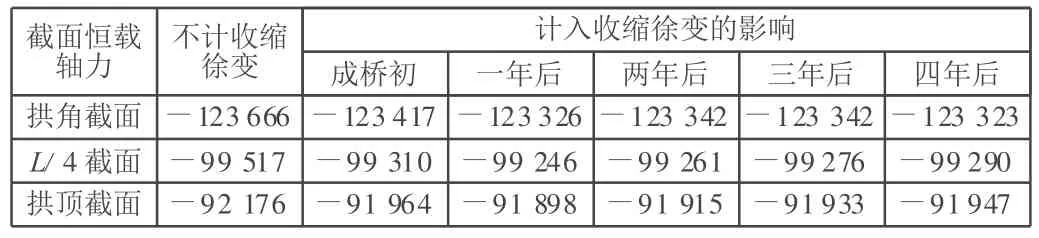
表1 全截面恒载轴力随时间变化比较 kN

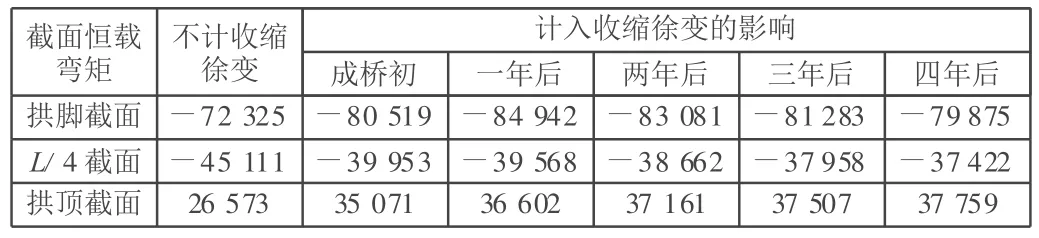
表2 全截面恒载弯矩随时间变化比较 kN◦m

由表1,表2可知,混凝土收缩徐变对结构全截面轴力基本上无影响,但对全截面弯矩有较大的影响。在成桥初期,对拱脚、L/4、拱顶截面,计入混凝土收缩徐变影响的全截面弯矩比不计混凝土收缩徐变影响的全截面弯矩要分别大10%,小13%与大24%。

为更清楚了解混凝土收缩徐变对各控制截面内钢管与混凝土单元各自内力的影响,将钢管与混凝土所承受的内力分别进行分析。将不计混凝土收缩徐变与计入混凝土收缩徐变,以及成桥初期与1年～4年后等时期的各控制截面的内力值列出,见表3～表6。

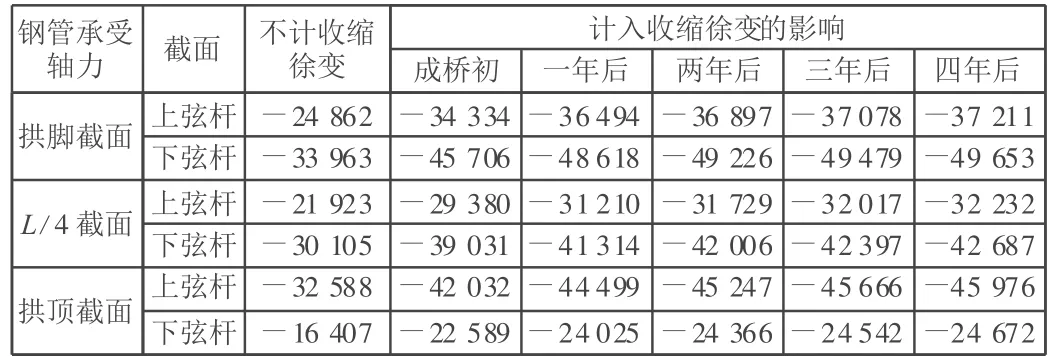
表3 钢管恒载轴力随时间变化比较 kN

表4 钢管全截面恒载弯矩随时间变化比较 kN◦m

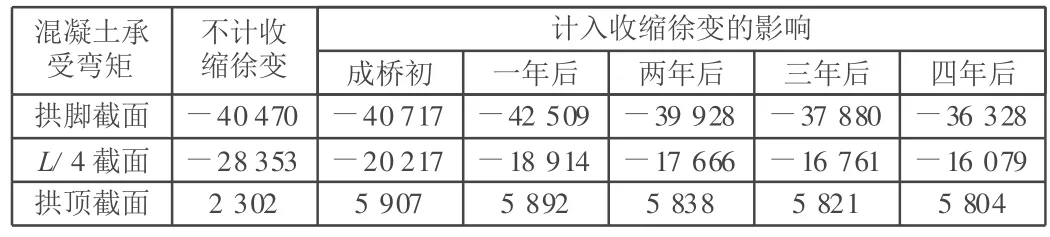
表5 混凝土全截面恒载弯矩随时间变化比较 kN◦m

表6 混凝土恒载轴力随时间变化比较 kN

由表3～表6可知,混凝土收缩徐变对各控制截面钢管与混凝土单元间的内力重分配有很大影响。成桥初,计入混凝土收缩徐变后钢管单元所承受的轴力要比不计混凝土收缩徐变的钢管单元所承受的轴力大22%～28%;而混凝土单元所承受的轴力则相反,计入混凝土收缩徐变后的混凝土单元所承受的轴力要比不计混凝土收缩徐变的混凝土单元所承受的轴力小43%～78%(除拱脚的上弦杆截面外),即表明混凝土收缩徐变使钢管与混凝土单元所承受的轴力发生了重分布,钢管单元所承受的轴力增加,混凝土单元所承受的轴力减小。

混凝土收缩徐变对钢管所承受的轴力影响主要在成桥以后的一年内,一年以后基本趋于稳定;混凝土收缩徐变对混凝土单元所承受的轴力影响主要在成桥后的两年内,两年以后基本趋于稳定。

混凝土收缩徐变对全截面恒载弯矩有较大的影响,成桥时,计入混凝土收缩徐变后钢管单元的弯矩值比不计混凝土收缩徐变的弯矩值大15%～20%,对于拱脚与拱顶截面混凝土单元的弯矩值比不计混凝土收缩徐变的弯矩值分别大1%和61%,混凝土收缩徐变使钢管单元所承受的弯矩值增大而混凝土单元所承受的弯矩值减小的趋势。

混凝土收缩徐变对钢管所承受的弯矩的影响主要在成桥以后的两年内,两年以后基本趋于稳定;混凝土收缩徐变对混凝土所承受弯矩影响主要在成桥后的四年内,四年以后基本趋于稳定。

1.2 混凝土收缩徐变对截面应力的影响

混凝土收缩徐变对各控制截面钢与混凝土之间内力重分布有较大的影响,计入混凝土收缩徐变后,对各控制截面的钢管与混凝土的应力也有较大的影响。

由表7可知,计入混凝土收缩徐变对钢管的应力有较大的影响。计入混凝土收缩徐变后,在成桥初各控制截面钢管的应力增加22%～30%,一年以后,钢管的应力增加6%左右,以后每年又增加2%左右,计入混凝土收缩徐变后,钢管应力增加主要集中在成桥后的一年内,一年以后基本趋于稳定。

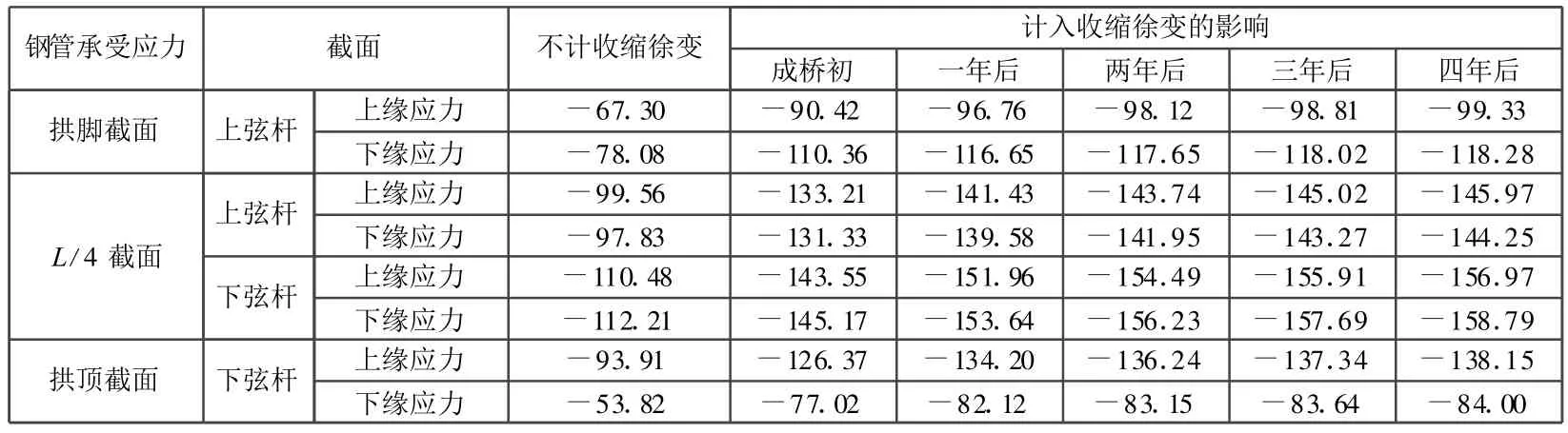
表7 结构各控制截面的钢管应力随时间变化值 MPa

表8 结构各控制截面的混凝土应力随时间变化值 MPa

由表8可知,计入混凝土收缩徐变后,对于各控制截面成桥初的应力比不计混凝土收缩徐变要减少33%以上,拱顶截面下弦杆的混凝土下缘应力减少131%,其他截面的应力均减少33%～97%。而拱脚截面上弦杆上缘处的混凝土应力在计入混凝土收缩徐变的影响后,由原来的压应力变为拉应力。在成桥后的两年内,混凝土的应力基本趋于稳定。

2 结语

1)混凝土收缩徐变对结构体系的全截面轴力基本上无影响,但对结构的全截面弯矩有较大的影响。

在成桥初期,对拱脚、L/4及拱顶截面,计入混凝土收缩徐变影响的全截面弯矩比不计混凝土收缩徐变影响的全截面弯矩要分别大10%,小13%与大24%。

2)对于各控制截面,混凝土收缩徐变使钢管与混凝土间的内力与应力发生重分布。

成桥初,混凝土收缩徐变引起钢管所承受的轴力与全截面弯矩增加 15%～28%,引起混凝土所承受轴力减小43%～78%,引起拱脚与拱顶截面混凝土所承受的全截面弯矩增大1%和61%。混凝土收缩徐变引起钢管的应力成桥后4年内增加了10%,引起混凝土的应力减小18%～44%左右。

[1]蔡绍怀.钢管混凝土结构[M].北京:中国建筑科学研究院,1992.

[2]李国平,张哲元.钢—混凝土组合桥混凝土收缩徐变分析[J].结构工程师,1999(1):34-35.

[3]谢肖礼.钢管混凝土拱桥收缩徐变对任意截面应力重分布的影响[D].南宁:广西大学博士论文,2002:6.

[4]王成斌.桥梁加固新老混凝土收缩差分析研究[J].山西建筑,2009,35(10):54-55.