初始扰动对于气液界面Rayleigh-Taylor不稳定性发展的影响
黄文斌,邹立勇,刘金宏,谭多望,张光昇
(中国工程物理研究院流体物理研究所冲击波物理与爆轰物理国防科技重点实验室,四川绵阳 621900)
0 引 言
两种不同密度的流体在重力或惯性力作用下的界面不稳定性问题称为Rayleigh-Taylor不稳定性(简称RT不稳定性)。RT不稳定性广泛存在于惯性约束聚变、超新星爆发、电磁内爆、水下爆炸等过程中并且起着重要作用,因而受到广泛重视。
俄罗斯实验物理研究院为对RT不稳定性发展过程进行研究,在20世纪80年代逐步建立了一套新颖的RT不稳定性实验方法——果冻实验方法[1-5]。该方法利用了果冻有限的强度能使其保持自身形状,并且在高压气体加载下果冻可视为流体(其强度可以忽略)的特性,通过模具能够实现对复杂构形及其初始扰动界面的精确控制。另外,果冻实验的加载方式一般采用压缩气体驱动或乙炔-氧气混合气体爆轰驱动,加上果冻本身是透明的,因而可以方便地采用可见光测试技术,通过高速相机可以获得实验过程的高分辨率图像。果冻实验方法可以研究在不同加载方式(如平面加载、外爆加载以及内爆加载)下多种结构(如平面、柱形以及半球形等)的RT不稳定性现象。
采用乙炔-氧气混合气体爆轰驱动带有二维单模周期扰动的果冻层,利用高速摄影记录扰动的发展过程,通过实验对比具有不同波长和振幅的初始扰动界面RT不稳定性发展的差异。
1 实验装置与方法
图1为实验装置示意图。装置的主体为方形有机玻璃管,该管是由若干内截面尺寸为40mm×40mm的有机玻璃方块组合而成,并且其内外表面经过光学抛光处理。果冻层将有机玻璃管分成两部分,上半部分为空气并与外界连通,下半部分为通过气嘴充入的乙炔和氧气混合气体,实验时气嘴关闭。果冻层的厚度为18 mm,其下表面(与混合气体的接触面)预制有二维正弦扰动,为了使果冻层在加速运动过程中保持平整,在果冻层上表面放置了一片厚度2 mm的聚四氟乙烯薄片。在端盖中心处有一个电火花隙,用于起爆乙炔和氧气混合气体(简称混合气体)。
实验主要过程如下:首先将一块有机玻璃方块放在刻有初始扰动的模板上,形成一个方槽,并向其中倒入3.5%的明胶溶液;待明胶凝固成型后,取掉模板,得到具有初始扰动界面的果冻层,再将该有机玻璃方块嵌入装置中;然后打开气阀充入混合气体(乙炔氧气体积比为1:2.5),为了将气室内空气置换干净,混合气体充入量不小于气室容积的10倍,充气完毕后关闭气阀;最后在电火花隙两端加10 kV脉冲电压,产生电火花起爆混合气体,反应产生高压气体驱动果冻层向上加速运动。实验采用CCD相机(Photron FASTCAM-APX)记录果冻层界面演化过程,相机的幅频为2×104幅/s,分辨率为512×256。
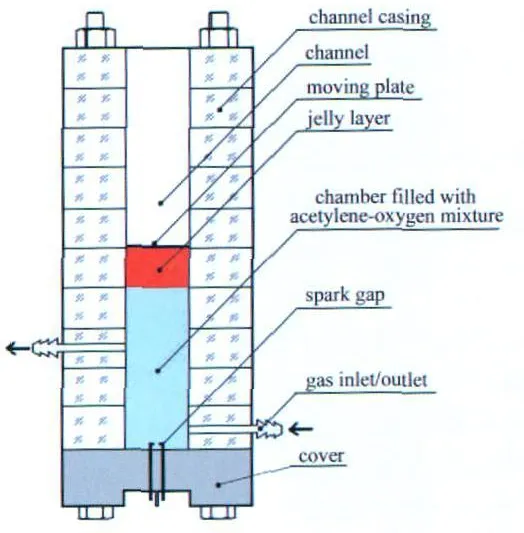
图1 实验装置示意图Fig.1 Schematic of experimental facility

图2 3种初始扰动Fig.2 Schematic of initial perturbations
实验中初始扰动界面为二维单模余弦扰动(h= acos(2πy/λ),-20mm≤y≤20mm,λ为波长,a为振幅),为认识初始扰动波长和振幅对于界面扰动发展的影响,采用了图2所示3种初始扰动。
2 实验结果与分析
CCD相机记录的果冻层界面演化过程如图3所示。图3显示了3种不同初始扰动在几个相同时刻界面扰动的发展情况。
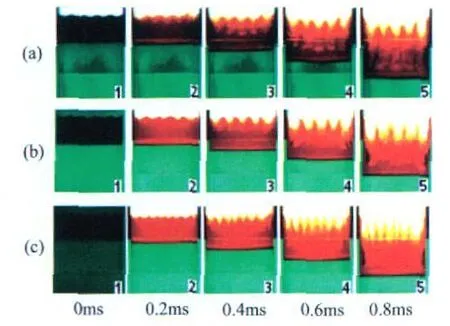
图3 气相爆轰驱动果冻层加速运动的分幅图像Fig.3 Photochronography of the jelly layer accelerated by the gas explosive mixture products(perturbations grow at unstable interface)

式中:Atwood数A=(ρ1-ρ2)/(ρ1+ρ2),ρ1、ρ2分别是重流体和轻流体的密度;g是加速度;Z是界面移动的距离。下标i表示轻流体混入重流体的气泡(i=b)或者表示重流体侵入轻流体的尖钉(i=s)。αi是需要通过实验确定的常数。实验中,A≈1,公式(1)可简化为

根据Read[6]和Youngs[7]提出的经典公式,在非线性阶段RT不稳定性混合区的气泡深度和尖钉高度可描述为:
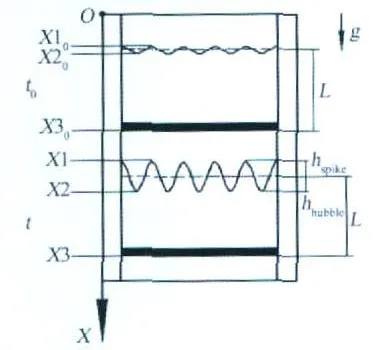
图4 实验图像分析示意图Fig.4 Schematic of experimental images analysis
实验结果的处理方法如图4所示,果冻层初始扰动界面的平衡位置到聚四氟乙烯薄片底部距离为L,对于不可压的果冻层,L在实验过程中是不变的。重流体侵入轻流体的尖钉高度为其顶端到平衡位置的距离为hs,轻流体混入重流体的气泡深度为其顶端到平衡位置的距离为hb,则有:hs=X3-X1-L;hb=L-(X3-X2);Z=X3-。
进一步分析发现:在(a)、(b)、(c)3种实验中,扰动发展进入非线性阶段时对应的扰动幅度h=hs+hb分别为10.2、10和12.55 mm,实验数据显示在线性阶段较短波长的扰动发展得更快,并且波长是影响扰动发展的主要因素,初始振幅的影响可以忽略。
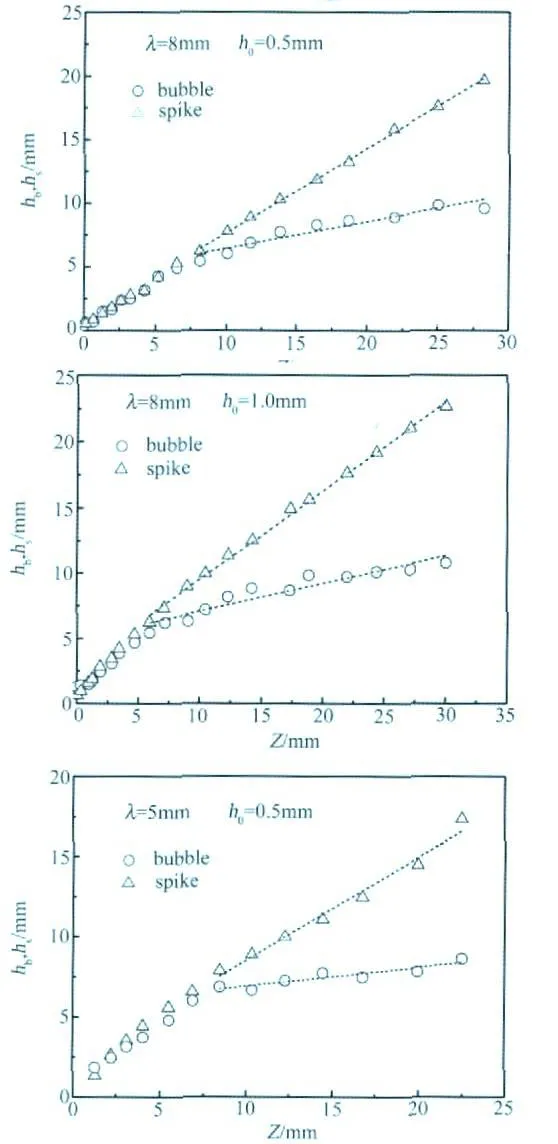
图5 尖钉高度hs和气泡深度hb随界面移动距离Z变化曲线Fig.5 Spike and bubble amplitude vs displacement for various initial perturbations
通过选取非线性阶段的实验数据进行线性拟合,结合公式(2),得到尖钉增长系数αs和气泡增长系数αb,如表1所列。
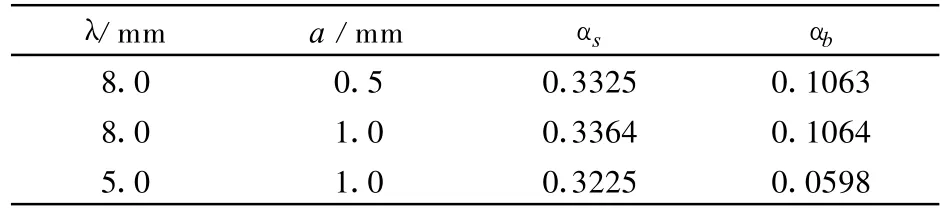
表1 实验所得尖钉增长系数αs和气泡增长系数αbTable 1 The experimental results of αsand αb
对于初始扰动界面为二维单模余弦扰动的情形,实验结果表明:初始扰动波长λ=8 mm时,初始振幅a的变化对于非线性阶段尖钉和气泡的增长几乎没有影响;初始扰动振幅a=1mm时,初始波长λ的增加有利于尖钉和气泡增长,其中对于气泡的影响尤为明显,初始波长l增加80%,气泡增长系数αb相应地增加了78%,基本呈线性关系。综上所述,在非线性阶段,波长仍然是影响扰动发展的主要因素,与线性阶段不同的是,较长波长的扰动发展更快,并且波长仅对气泡发展产生明显影响作用,对尖钉发展的影响可忽略;初始扰动振幅对于扰动发展的影响仍然可以忽略。俄罗斯实验物理研究院Meshkov等人的研究结果也表明,在线性阶段初始扰动波长越短,扰动增长速度越快;从线性阶段到非线性阶段、进而到湍流混合阶段,扰动幅度增长速度减小,并且增长速度逐步由较长波长的谐波来主导。研究结果验证了该结论。
3 小 结
利用平面果冻层实验方法开展了二维单模余弦初始扰动波长和振幅对界面RT不稳定性发展影响规律的实验研究,初步得到下列结论:波长是影响界面扰动发展的主要因素,并且在不同阶段影响的模式不同。在线性阶段,较短波长的扰动发展更快;相反,在非线性阶段,较长波长的扰动发展的更快。初始振幅对于扰动幅度发展的影响,无论在线性阶段还是非线性阶段都是可以忽略的。
[1]M ESHKOV E E,NEVM ERZHITSKY N V.About turbulent mixing dynamics at unstable boundary of liquid layer,accelerated by compressed gas[C]∥Proceedings of the 3rd international workshop on the physics of compressible turbulent mixing,1991:467-475.
[2]M ESHKOV E E,NEVM ERZHITSKY N V.Jelly technique applications in evolution study of hydrodynamic instabilities on unstable plane and cylindrical surfaces[C]∥Proceedings of the fifth international workshop on the physics of compressible turbulent mixing,1996:243-250.
[3]WEIR S T,CHANDLER E A,GOODWIN B T.Rayleigh-Taylor instability experiments examining feedthrough growth in an incompressible,convergent geometry[J].Phy.Rev. Lett,1998,80(17):3673-3676.
[4]ANDRONOV V A,M ESHKOV E E.Computational and experimental studies of hydrodynamic instabilities and turbulent mixing[R].DE95006837/HDM.
[5]BAKHRAKH S M,DRENNOV O B.Hydrodynamic instability in strong media[R].UCRL-CR-126710.
[6]READ K I.Experimental investigation of turbulent mixing by Rayleigh-Taylor instability[D].Physica D,1984,12:45-58.
[7]YOUNGS D L.Modeling turbulent mixing by Rayleigh-Taylor instability[D].Physica D,1989,37:270-287.

