基于传染病疫情防控机理的应急物资需求分析＊

辜 勇

（武汉理工大学物流工程学院 武汉 430063）

0 引 言

突发事件的救援救助活动需要大量应急物资，应急物资管理已成为应急管理的重要组成部分.对应急物资管理的研究主要集中在需求分析［1－2］、储备规划［3－4］和运输调度［5－6］等方面.

重大传染病疫情是一类典型的公共卫生事件，传染病疫情发生后所需求的应急物资主要是疫苗、治疗药品等医疗物资，目前针对传染病疫情的应急需求分析研究较少.卢书成等［7］提出了3类传染病扩散模型，通过描述传染病传播过程，得到感染人群的变化规律；周效良［8］对一类传染病扩散模型进行研究，得到了全局渐进稳定解的充分条件；Xu Jingjing［9］研究了具有多个疫区和多个应急配送中心的疫苗配送最优方案，用SIQR模型来描述传染病的扩散规律，在对各疫区进行聚类的基础上建立了动态的疫苗配送模型.

由于传染病疫情的扩散性引起应急物资需求的持续变化，因此合理估计疫情变化是需求分析的关键，将该问题视为一个多阶段状态变化问题，通过分析病人状态变化得到应急医疗物资的需求.

1 需求分析模型

1.1 假设及符号说明

令应急开始时间为t＝0，结束时间t＝l；x（t）为在t时刻到达的应急物资数量；令1个感染疫情的病人需要1个单位的应急物资（如治疗药品等）.

疫情防控部门对重大传染疾病会采取隔离措施，令γ（t）为t时刻疫情防控部门对前一时刻（t－1）未隔离的感染病人进行隔离的比例，显然γ（0）＝0，随着疾病的传播，社会公众的对疾病认知度和疫情防控部门的工作力度逐步提升，隔离的比例会逐渐提高到接近1的数值；病人的状态及数量变化如图1所示.

令r（t）为t时刻感染疫情但未被隔离的病人数量，则r（0）表示被感染的初始病人数.

没有被隔离的病人会通过接触健康人群传染疾病，假设单位时间每个病人平均传染人数为μ；被隔离的病人不会传染疾病，而且只有被隔离的病人能够接受救治；如果在发病期间未及时得到应急物资进行治疗，病人会死亡，假设病人从感染发病到死亡的时间为φ.

图1 重大传染病疫情的病人状态变化示意图

记a（t）为在t时刻新增感染病人数量，显然a（0）＝0，则

为区分未隔离病人的染病时间，记b（t）t为在t时刻未隔离病人中保持原有状态（不是在t时刻死亡、也不是t时刻的新增病例）的病人数量，上标表示其染病时间，则在k时刻有φ批病人，包括 b（k）k、b（k）k－1，…，b（k）k－φ＋1，其 中：b（k）k－1，…，b（k）k－φ＋1是从k－1时刻继承下来的，即b（k）k－1＝b（k－1）k－1，并且向k＋1时刻累积，即

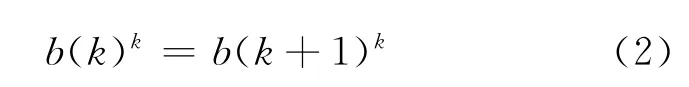
记c（t）为在t时刻未隔离病人中死亡的人数，b（k）k－φ＋1在k＋1时刻成为死亡人数，即

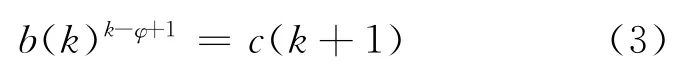
可以看出在k时刻死亡的病人一定来自于k－φ时刻的新增感染病人.

在这种继承和累积的过程中，处于保持状态的病人数量会发生变化，因为该群体是采取隔离措施的对象；在k时刻对a（k－1）和b（k）k－1，…，b（k）k－φ＋1的那些病人群体采取隔离措施有3种策略，悲观策略下认为被隔离病人首先来自于a（k－1），然后依次从b（k）k－1，…，b（k）k－φ＋1选取被隔离病人；中立策略下认为按隔离比例分别从a（k－1）和b（k）k－1，…，b（k）k－φ＋1选取被隔离的病人；乐观策略下认为按顺序优先从b（k）k－φ＋1，…，b（k）k－1，a（k－1）选取被隔离的病人；因为应急管理要作最坏的打算，选择悲观策略进行分析，实际上在后面的计算中发现悲观策略会导致物资需求的增加.记e（k）k为k时刻被隔离病人中由于药品不足而等待的人数，显然在k时刻被隔离的等待病人有φ 批，数量分别为e（k）k，e（k）k－1，…，e（k）k－φ＋1.e（k）k为k时刻被隔离人数，即e（k）k＝r（k）·γ（k），e（k）k－1，…，e（k）k－φ＋1为k－1时刻累积到k时刻的，悲观策略下，

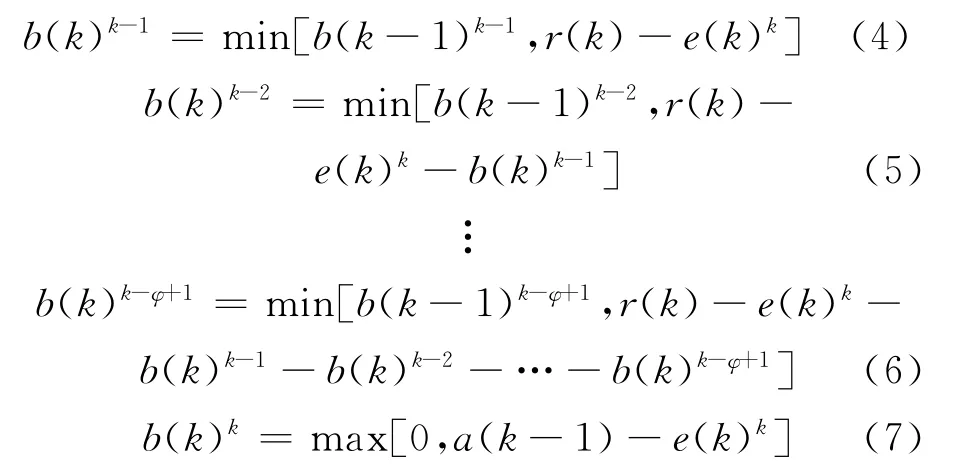
根据r（t）的定义，则

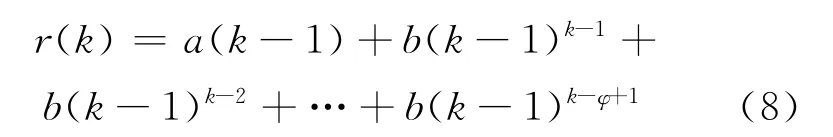
应急救治药品到达时，首先提供给染病时间最早的病人进行救治，也就是从上标最小的e（k）k－φ＋1开始依次分配物资，直至全部满足需求.

k时刻治愈病人数量取决于当期到达的物资数量和等待药品的病人数量，记d（t）为在t时刻被隔离病人中治愈的人数，即

若k时刻到达的应急物资数量不能完全满足等待病人需求，等待病人数量累积到k＋1时刻，e（k）k变为e（k＋1）k，e（k）k－1变为e（k＋1）k－1，以此类推.

如果k时刻到达的应急物资数量不能满足e（k－1）k－φ的需求，会导致病人死亡，记f（t）为在t时刻被隔离病人中死亡的人数，即

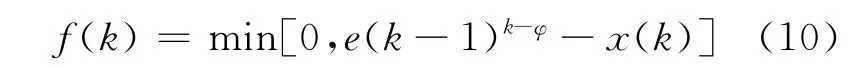
为避免隔离病人出现死亡，每阶段到达的应急物资应能够治疗将在下一阶段死亡的病人，令q（t）表示t时刻应急物资需求数量的最小值，则

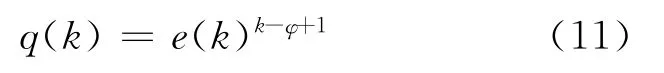
1.2 计算过程

综上所述，计算k时刻模型各参量步骤如下.

步骤1 计算需隔离病人数量和未隔离病人中的死亡人数.

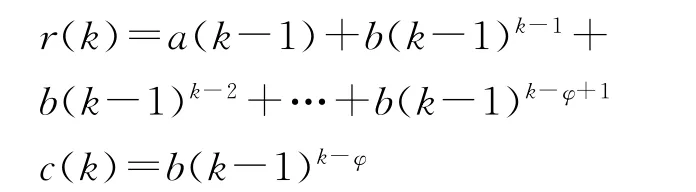
步骤2 计算e（k）k和b（k）k.

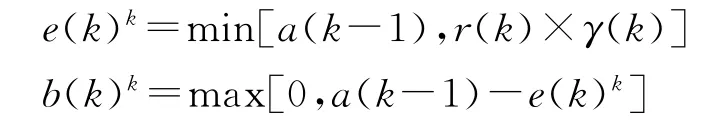
步骤3 当r（k）×γ（k）≤a（k－1）时，

当r（k）×γ（k）＞a（k－1）时，按悲观策略分配隔离病人，

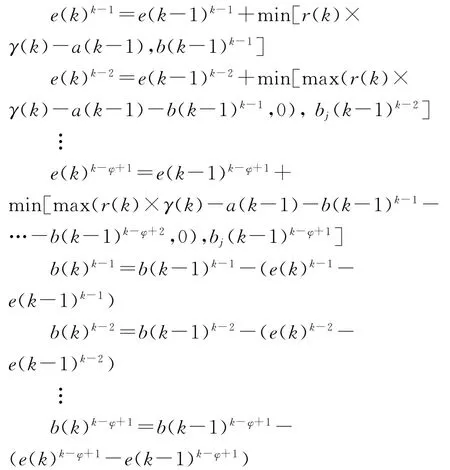
步骤4 需求分析时，暂时不考虑有应急物资到达，即d（k）＝0，f（k）＝e（k－1）k－φ.

步骤5 计算新增病人数.a（k）＝［b（k）k＋b（k）k－1＋b（k）k－2＋…＋b（k）k－φ＋1］·μ

2 求解算例

以μ＝10，φ＝2，r（0）＝2为例计算传染病疫情的扩散及在不提供应急药品情况下的死亡病例，其他给定条件及计算结果见表1.由于φ＝2，表1中未隔离病人保持数量分为本期保持和上期保持，隔离病人中分为本期等待和上期等待；表1中最后一列数据即每期的应急需求q（k）.

t＝0时，初始病人数2，隔离比例为0，新增病人20，保持原状态病人2.

t＝1时，需隔离病人＝上期未隔离病人保持人数2＋上期新增病人数20＝22，隔离比例为0.5，隔离病人中本期等待人数＝22×0.5＝11，本期未隔离病人中的本期保持人数＝max（0，上期新增病人数量20－本期隔离病人数11）＝9，本期未隔离病人中的上期保持人数＝min（上期未隔离病人中的本期保持数量2，本期需隔离病人数22－隔离病人中本期等待人数11）＝2，新增病人数＝本期未隔离病人数（9＋2）×10＝110.

t＝2时，未隔离病人死亡人数＝上期未隔离病人中的上期保持病人数2，需隔离病人＝上期未隔离病人本期保持人数9＋上期新增病人数110＝119，隔离比例为0.8，隔离病人中本期等待人数＝119×0.8＝95，本期未隔离病人中的本期保持人数＝max（0，上期新增病人数量110－本期隔离病人数95）＝15，本期未隔离病人中的上期保持人数＝min（上期未隔离病人中的本期保持数量9，本期需隔离病人数119－隔离病人中本期等待人数95）＝9，新增病人数＝本期未隔离病人数（15＋9）×10＝240，隔离病人中的上期等待人数＝上期隔离病人中的本期等待人数11.

t＝3时，未隔离病人死亡人数＝上期未隔离病人中的上期保持病人数9，需隔离病人＝上期未隔离病人本期保持人数15＋上期新增病人数240＝255，隔离比例为0.9，隔离病人中本期等待人数＝255×0.9＝229，本期未隔离病人中的本期保持人数＝max（0，上期新增病人数量240－本期隔离病人数229）＝11，本期未隔离病人中的上期保持人数＝min（上期未隔离病人中的本期保持数量15，本期需隔离病人数255－隔离病人中本期等待人数229）＝15，新增病人数＝本期未隔离病人数（15＋9）×10＝260，隔离病人死亡人数＝上期隔离病人中的上期等待人数11，隔离病人中的上期等待人数＝上期隔离病人中的本期等待人数95.

依次计算t＝4，5，6，…，直至没有新增病人、也没有死亡病人时结束.

表1 传染病疫情扩散时病人数量变化的计算示例

观察表1发现初始病人只有2人的情况下，通过每单位时间（天）传播10人，即使在有隔离防控措施下，可造成感染病人数量达880人，若没有治疗药品会造成839人死亡；表2列出了在其他条件不变的情况下，γ（t）取值改为｛0，0.4，0.7，0.85，0.9，0.95，0.96，0.97，0.98，0.99，0.99，1，1｝时的计算结果；表3列出了在其他条件不变的情况下，μ改为12时的计算结果.

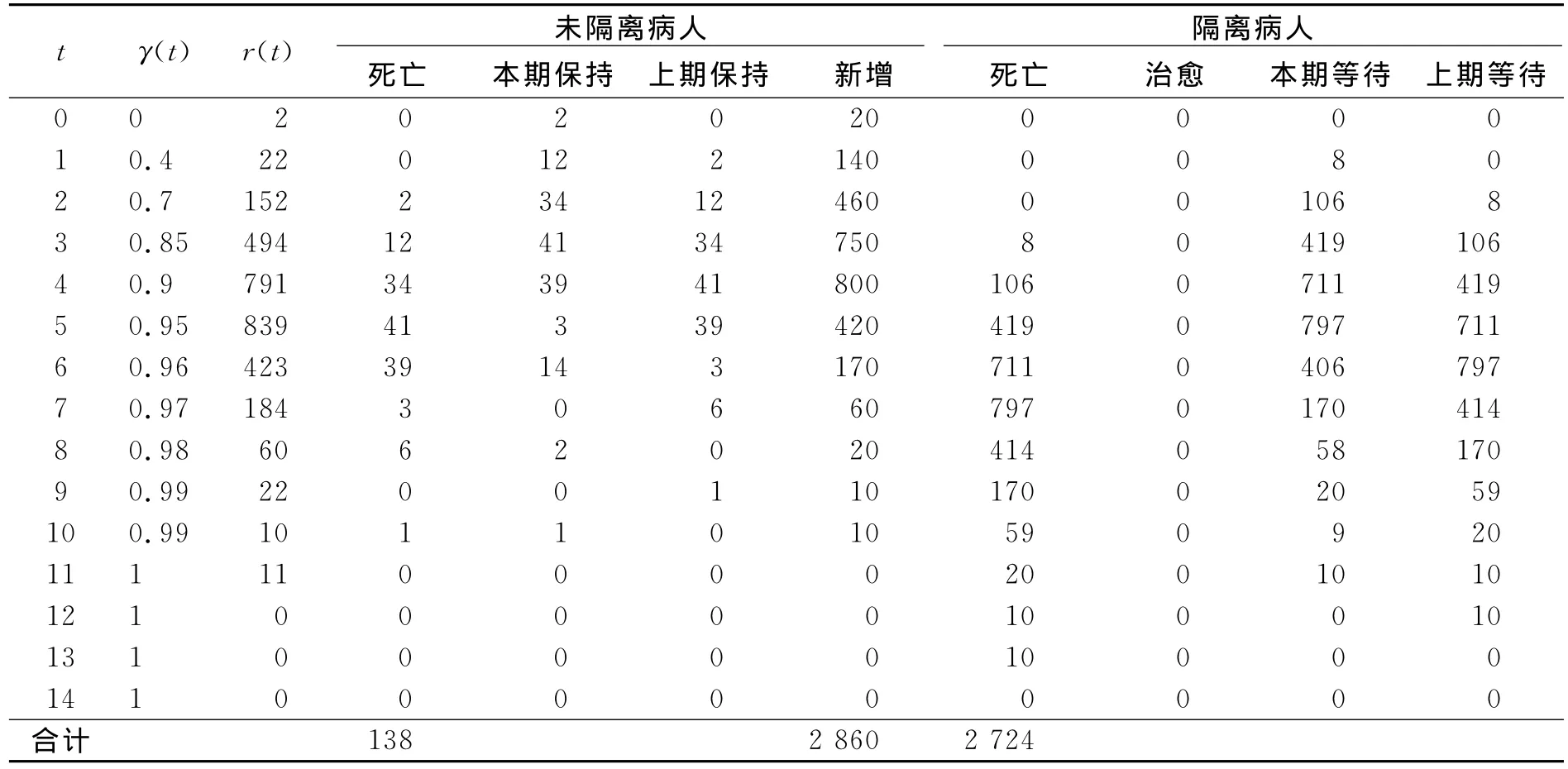
表2 γ（t）变化时的计算结果

对比表1～3发现，衡量隔离措施效果的参数γ（t）和描述疫情传播扩散状态的参数μ的取值较小变化，对计算结果有很大影响，如表2中，γ（t）的取值比表1稍小，导致新增传染病人和死亡病例分别增加到2 860人和2 724人；表3中，μ增加2个单位，也导致新增传染病人和死亡病例成倍增长，达到1 740人、1 671人.

3 结 束 语

在应对传染病疫情这一类突发公共卫生事件时，要合理估计应急医疗物资需求，通过描述传染病疫情变化扩散的态势，建立了应急医疗物资需求模型.求解算例显示，通过设定2个参数γ（t）和μ，可以得出病人状态变化趋势，为应急医疗物资的调度提供依据.

表3 μ变化时的计算结果

［1］王成敏，孔昭君，杨晓珂.基于需求分析的应急资源结构框架研究［J］.中国人口·资源与环境，2010，20（1）：44－49.

［2］傅志妍，陈 坚.灾害应急物资需求预测模型研究［J］.物流科技，2009，（10）：11－13.

［3］Jia Hongzhong，Ordónez F，Maged M.Solution approaches for facility location of medical supplies for large－scale emergencies［J］.Computers ＆Industrial Engineering，2007，52（2）：257－276.

［4］田依林.基于FAHP法的应急物资储备库选址研究［J］.武汉理工大学学报：交通科学与工程版，2010，34（2）：354－357.

［5］Jotshi A，Gong Qiang，Batta R.Dispatching and routing of emergency vehicles in disaster mitigation using data fusion［J］.Socio－Economic Planning Sciences，2009，43（1）：1－24.

［6］柴秀荣，王儒敬.多出救点、多物资应急调度算法研究［J］.计算机工程与应用，2010，46（6）：224－226.

［7］卢书成，徐国通，丁岩峰，等.传染病扩散问题的研究［J］.牡丹江医学院学报，2006，27（1）：13－16.

［8］周效良.一类传染病扩散模型的研究［J］.电力学报，2002，17（3）：161－165.

［9］Xu Jingjing，Wang Haiyan.Dynamic vaccine distribution model based on epidemic diffusion rule and clustering approach［J］.Journal of Southeast University：English Edition，2010，26（1）：132－136.