一种GPS车辆定位系统中的自适应滤波算法

田小静，李万军，谭婕娟

TIAN Xiao-jing, LI Wan-jun, TAN Jie-juan

（西安航空职业技术学院 自动化工程系，西安 710089）

一种GPS车辆定位系统中的自适应滤波算法

An adaptive filtering algorithm of GPS vehicle positioning system

田小静，李万军，谭婕娟

TIAN Xiao-jing, LI Wan-jun, TAN Jie-juan

（西安航空职业技术学院 自动化工程系，西安 710089）

针对机动载体的“当前”统计模型在GPS车辆定位系统中存在的问题，基于动态GPS定位的精度取决于对动态载体扰动和观测异常扰动的认知和控制的原理，提出了一种基于“当前”统计模型的均值和方差自适应滤波算法。通过仿真试验结果证明，该算法不仅可以提高定位精度，而且能有效地控制观测异常和动态扰动异常对定位精度的影响。

全球定位系统（GPS)；Kalman滤波；自适应滤波；“当前”统计模型

0 引言

GPS在动态定位、动态监控、导航及测量等领域已获得广泛的应用[1]。车辆在运动中的定位属于动态定位过程，一般都选用GPS组合系统进行动态定位。文献[2]对车载GPS/DR组合导航系统进行了深入的分析，但该组合系统复杂、成本高，不能满足普通车辆定位导航的需要。单独使用GPS动态定位，系统简单、成本低，可以满足大众的需求，但动态定位数据中存在着影响定位精度的随机误差。卡尔曼滤波在动态数据处理中有着广泛的应用，它能克服一般的动态噪声对结果的影响[3]。同时，采用递推算法使计算简单快速，适合实时计算处理。但是可靠的Kalman滤波算法要求有可靠的、切合实际的车辆运动模型和随机干扰模型。然而车辆在运行过程中难以确保规则，因而精确的、符合实际的车辆运动模型的构造是解决车辆定位问题的关键。

为了满足实际车辆的定位精度，必须建立足够准确的数学模型，进一步控制载体扰动和观测异常扰动的影响，为此，本文提出目前比较合理、且更切合实际车辆运动情况的机动载体的“当前”统计模型进行自适应Kalman滤波算法。仿真结果表明，应用该模型和算法，有效提高了GPS动态定位的准确性和实时性，与改进前相比车辆导航定位系统的精度和实用性均得到明显提高。

1 数学模型的建立

1.1 系统方程的建立

近年来有不少学者对机动载体运动模型进行了研究，内容各具特点，建立的各种模型包括微分多项式模型、常速度模型、常加速度模型、时间相关模型（Singer模型、二阶时间相关模型、高阶时间相关模型）、半马尔柯夫模型、Noval统计模型及机动载体的“当前”统计模型[4]。对于载体在实际中的运动并不可能属于等速或等加速度范围的运动。Singer模型为零均值模型，机动加速度的零均值特性对于模拟机动目标来说根本不合理，对于快速机动的情况，将引起较大的模型误差。Kendrick[5]等把机动目标法向加速度的大小描述为非对称分布的时间相关随机过程的Novel统计模型，该模型被认为是现代载人飞行器的逃避机动的典型模型[6]，不适合于车辆运动模型。车辆运动模型需考虑加速度的分布特性，当车辆正以某一加速度行驶时，下一时刻的加速度取值是有限的，且只能在“当前”加速度的邻域内，为此，Zhou等人提出了机动目标的“当前”统计模型[7]。该模型本质上是非零均值时间相关模型，其机动加速度的“当前”概率密度用修正的瑞利分布描述，均值为“当前”加速度预测值，即

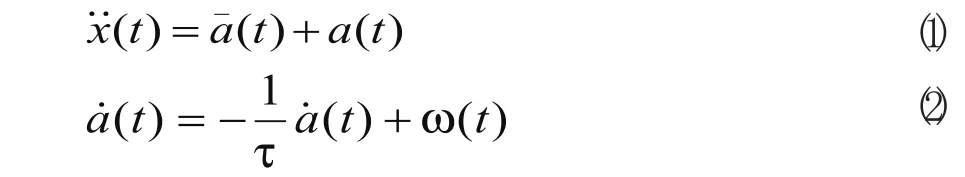
GPS定位存在随机误差，实践证明将GPS定位的各种误差源在各方向造成的总误差可等效为一阶马尔柯夫过程的有色噪声之和是行之有效的[7]。所以，由各种误差因素造成的两坐标轴方向上总的定位误差δe和δn可分别用一个马尔柯夫过程等效，则

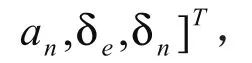
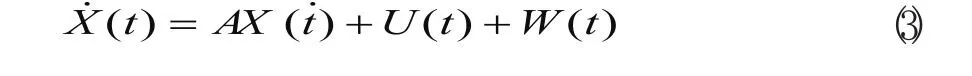
式(3)中，

ωe、ωn、ωee、ωen分别为（0，σe2）、（0，σn2）、（0，σee2）、（0，σen2）的高斯白噪声；τe、τn、τee、τen为马尔柯夫过程相关时间常数；分别为车辆东向和北向加速度分量的“当前”均值。

1.2 观测方程的建立

将GPS输出的位置和速度信息ye、yn取为观测量时，系统观测方程为：

其中， ωye、ωyn分别为量测噪声，假定分别为（0，σye2）、（0，σyn2）的高斯白噪声。

由(3)、(4)可以看出这是一典型的线性Kalman滤波模型，而且该系统可观测矩阵的秩等于系统状态变量的个数，故系统完全可观。

2 自适应滤波算法的建立

“当前”统计模型虽然是载体运动较合理的假设，但模型与载体的实际运动情况之间还是存在模型误差，且当滤波器中存在状态方程扰动异常时，定位解将会受到较大的影响。为了减少滤波误差，有效控制异常扰动的影响，进一步提高滤波器的动态性能，本文在“当前”统计模型的基础上提出了相应的均值和方差自适应滤波算法。该算法采用修正瑞利分布来描述机动加速度的统计特性[8]，因而更切合实际。同时，所假设的分布具有这样突出优点：分布随均值变化而变化，方差由均值决定。而且与其他方法不同，机动加速度是连续变化的，其均值等于“当前”时刻状态估计的加速度分量预测值。这样，在估计目标状态的同时，还可辨识出机动加速度均值。从而实时地修正加速度分布，并通过方差反馈到下一个时刻的滤波增益中，实现了闭环自适应滤波。

根据上述的系统方程及量测方程，设采样周期为T，通过离散化处理[8]，建立离散的Kalman方程如下：

状态预测：

滤波增益：

测量值修正：

在上式中，Φ(k,k-1)为系统的转移矩阵A(t)的离散化矩阵，

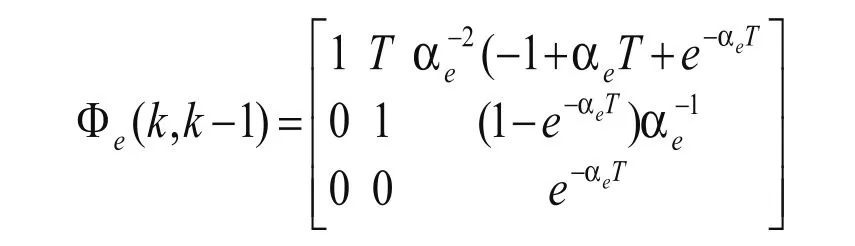
把加速度一步预测值看作“当前”加速度，通过上述滤波得：

在该自适应算法中，两个机动加速度均值及加速度方差的自适应确定方法如下：

如果将αe(k)和αn(k)的一步预测和分别看作kT瞬时的“当前”加速度，则利用载体随机机动加速度分别在东向和北向坐标轴上分量的均值，便可得到加速度的均值自适应算法。在上述(3)式中，由最优估计理论可知[7]，加速度状态变量α(t)的最优估计正是整个过去观测γ(t)的条件均值，如果可直接从Kalman滤波中得到，则利用代替α(t)中的均值，便可得到状态变量α(t)的估计值与状态噪声ω(t)的均值之间的关系。另外，状态变量α(t)的估计值与状态噪声ω(t)的方差σω2之间的关系如下[9]：“当前”加速度为正时：

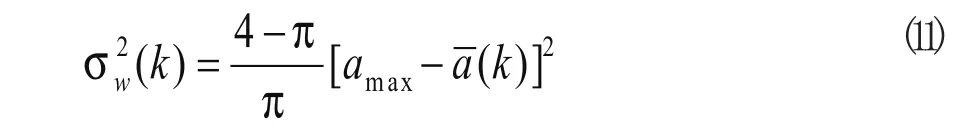
“当前”加速度为负时：

其中，αmax和α-max分别为估计目标可能发生的最大、最小机动加速度。

3 计算机仿真与分析

3.1 仿真条件

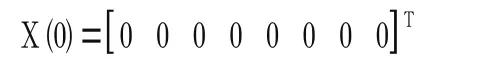
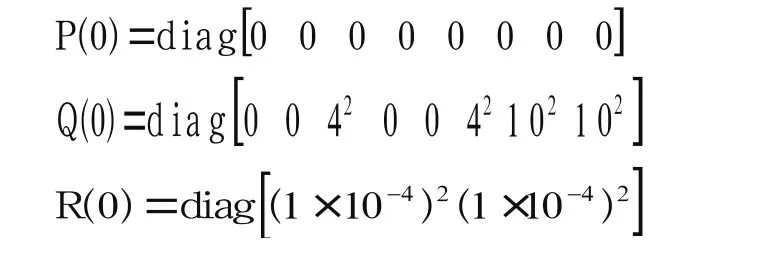
马尔柯夫过程相关时间常数τe=τn=1.0、τee=τen=0.5。假定车辆以的速度，沿π/4航向角变速运动，行驶500s。

3.2 仿真分析

由图1的系统位置误差曲线可知，采用经典Kalman滤波时，系统位置误差在±10m范围内，且误差始终在剧烈的震动。而采用自适应Kalman滤波，系统误差在±3.5m范围内，且平稳。

由图2的北向位置误差曲线可得知，经典Kalman滤波后，北向位置误差在±5m范围内，自适应Kalman滤波后，北向位置误差在±2.5m范围内。

综合图1和图2可得，北向位置和东向位置合成系统位置，在合成过程中，同时扩大了系统误差，自适应Kalman滤波有效地减小了系统误差，提高了定位精度。

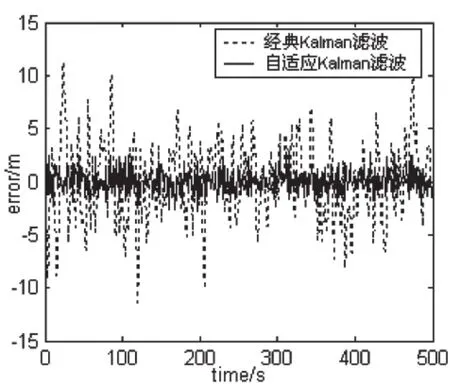
图1 系统位置误差

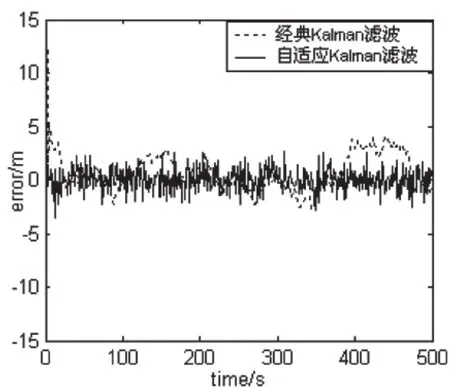
图2 北向位置误差

4 结论

综上可知，在GPS动态定位中，基于“当前”统计模型的Kalman滤波，采用修正瑞利分布来描述机动加速度的统计特性，更切合实际，这在一定程度上，有效的提高了GPS的动态定位函数模型的精度。此外，基于“当前”统计模型的自适应Kalman滤波算法相对于经典的Kalman滤波算法在精度和动态性能方面都有明显的改善，在估计目标状态的同时，还可辨识出机动加速度均值。从而实时的修正加速度分布，并通过方差反馈到下一个时刻的滤波增益中，实现了闭环自适应滤波。

[1] Da-jie,SHI Yi-min,GUO Jin-jun.The Theory about GPS and Data Process[M].Shanghai:Tongji University Press,1996.

[2] 万德均,房建成,王庆.GPS动态滤波的理论、方法及其应用[M].南京:江苏科学技术出版社,2000.

[3] 胡丛玮,刘大杰,姚连璧.带约束条件的自适应滤波及其在GPS定位中的应用[J].测绘学报,2002.31:40-44.

[4] 周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1991.

[5] Kendrick J D,Maybeck P S,Reid J G.Estimation of aircraft target motion using orientation measurements[J]. IEEE Transaction on Aerospace and Electronic Systems,1981,17(2):254-159.

[6] 潘平俊,冯新喜,赵晓明.机动目标模型研究与发展综述[J].情报指挥控制系统与仿真技术,2006.28(3):12-15.

[7] Zhon Hr,Kumanr KSP.A Current Statistical Model and Adaptive Algorithm for estimating Maneuvering Targets AIAA[J].Journal of Guidance,Control and Dynamics,1984,7(5):596-602.

[8] 付梦印,邓志红,张继伟.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2003.

[9] 王新龙,申功勋,丁杨斌.利用GPS进行车辆动态定位的自适应模型研究[J].控制与决策,2005,20(1):103-105.

TN911.72

A

1009-0134(2010)11(下)-0169-04

10.3969/j.issn.1009-0134.2010.11(下).57

2010-09-13

田小静（1977 -），女，讲师，学士，主要从事机电控制技术方面研究。