网络图形最短路径算法分析与研究

湛文红

（首钢工学院，北京100144）

1.引言

目前，在求网络图形最短路径的问题上主要有四种算法，它们是Dijkstra算法、逐次逼近算法、矩阵算法、Floyed算法，它们分别出现在数据结构、运筹学、图论等课程中。其中前两种算法都是求图上从某一点至另一点的最短路径，而后两种算法是求出网络图上所有节点之间的最短路径。由于这些算法分别出现不同的学科课程中，因此人们不易将它们进行统一的归纳总结与分析比较。

Dijkstra算法与逐次逼近算法解决的是从某一个节点到另一节点之间的最短路径问题，算法的时间复杂度是O(n2)。如果想得到每一对节点之间的最短路径，则需要多次调用算法进行计算。显然，这种方式对于求网络图中每一对节点之间的最短距离就显得过于麻烦。

矩阵算法与Floyed算法较好地解决了这方面的问题，它可以通过算法的一次调用直接计算出网络中每一对节点之间的最短路径值，因而弥补了前两种算法在这方面的不足。它们通过一个图的权值矩阵求出每两点间的最短路径矩阵。从图的带权邻接矩阵A=[a(i，j)]n×n开始，逐渐扩展，最终找到所有节点间的最短路径。矩阵算法与Floyed算法的时间复杂度是O(n3)。

事实上，许多人混淆了后两种算法，认为它们是同一个算法，原因是它们不但功能相同，而且都是采用矩阵运算的形式进行最短路径的求解。其实，它们在处理方法上还是有很大区别的，在此基础上分析它们的附加功能也是不同的。本文将着重对这两种算法进行分析与讨论，以求在实际应用中对读者起到参考借鉴的作用。

2.矩阵算法与Floyed算法的分析与研究

2.1 两种算法的说明

2.1.1 矩阵算法

矩阵算法的主要思想是首先构造初始距离矩阵，然后进行逐次迭代。首先进行第一次迭代，求出网络图中任意两个节点之间最多经过1个中间节点的最短距离；再进行第二次迭代，求出任意两个节点之间最多经过3个中间节点的最短距离；如此进行直至第k次迭代，求出任意两个节点间最多经过（2k-1）个中间节点的最短距离或当相邻两次迭

⑥最终得到任意两点间的最短路径值及其相应途经的节点序列。

此算法适用于所有无向图与有向图。

本人为此编制了程序以解释其原理。用以下有向图实例（如图1所示）来加以说明：

(1)定义图形

如图2所示，其中表格内的数值表示两点间的权值，空位置处表明两点之间没有直接路径。代结果相同的时候停止迭代过程。

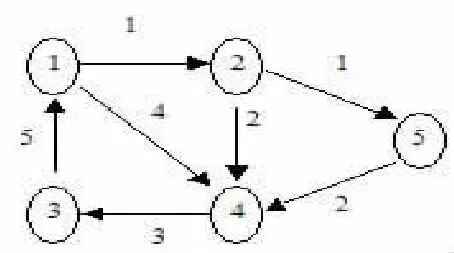
图1 实例

具体步骤：

①首先构造距离矩阵Dn×n（以距离为权的权值矩阵）。矩阵给出了所有节点之间只经过一步（一条边）的最短距离。

②设置途经的节点路径矩阵Rn×n内的所有元素rij(i，j=1…n)均为空字符。

③对距离矩阵进行如下的迭代运算：

D(r)=D(r-1)*D(r-1)=[dij]（第一次迭代r=1，以后逐次加1。）

式中：

n----网络节点数；

D(0)为初始的距离矩阵；

*----矩阵逻辑运算符，dij=m in[dik+dkj]（k=1，2，3，…，n）。dik，dkj----距离矩阵D(r-1)中的元素，分别为上次迭代后节点i、k之间、节点k、j之间的最短距离。dij为本次迭代后节点i，j之间经过k节点的最短距离（k=1，2，3，…，n）。

④保存本次迭代当前最短路径的途径节点序列。具体方法是：

如果本次迭代计算出的当前最短路径为dij=dik+dkj，则进行下面的操作：

如果为第一次迭代则令rij=“i k j”，否则，则令rij=rik&rkj(其中符号“&”为字符串连接运算符)。

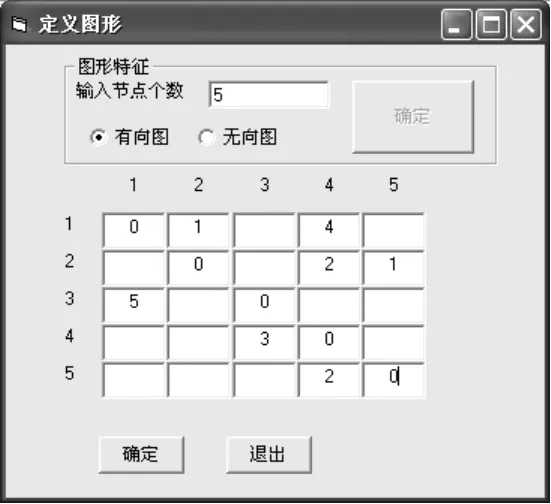
图2 定义图形

(2)生成网络图形邻接矩阵（如表1所示）

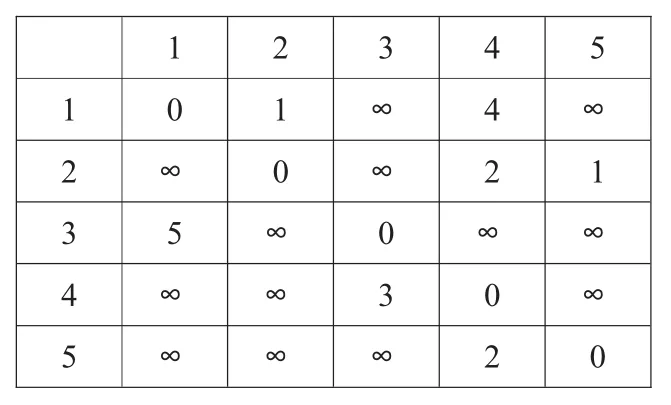
表1 邻接矩阵

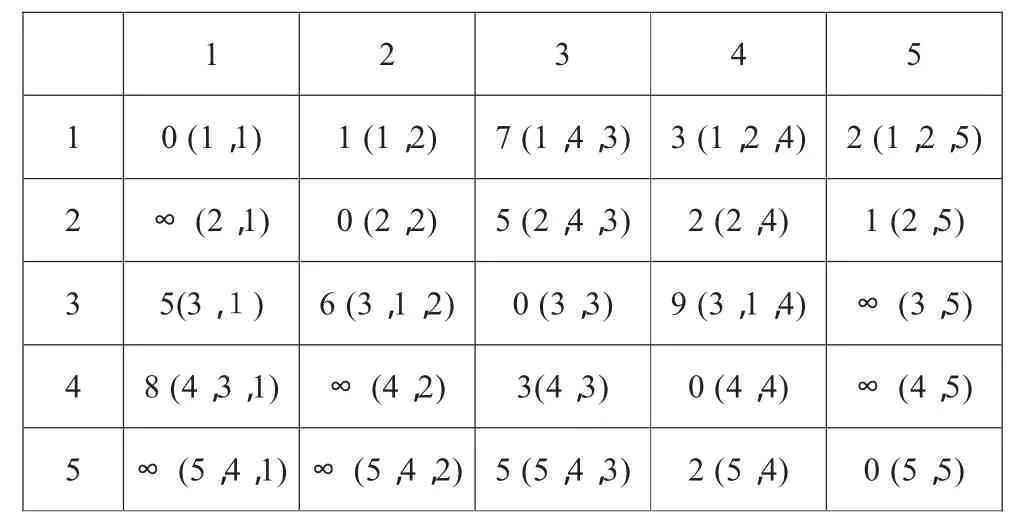
表2 第一次迭代后结果

(3)第一次迭代

第一次迭代的结果是两个节点之间最多跨接1个节点（如表2所示）。

注：其中“∞(n，m)”表示从n点到m点之间的距离为∞，以下相同。

(4)第二次迭代

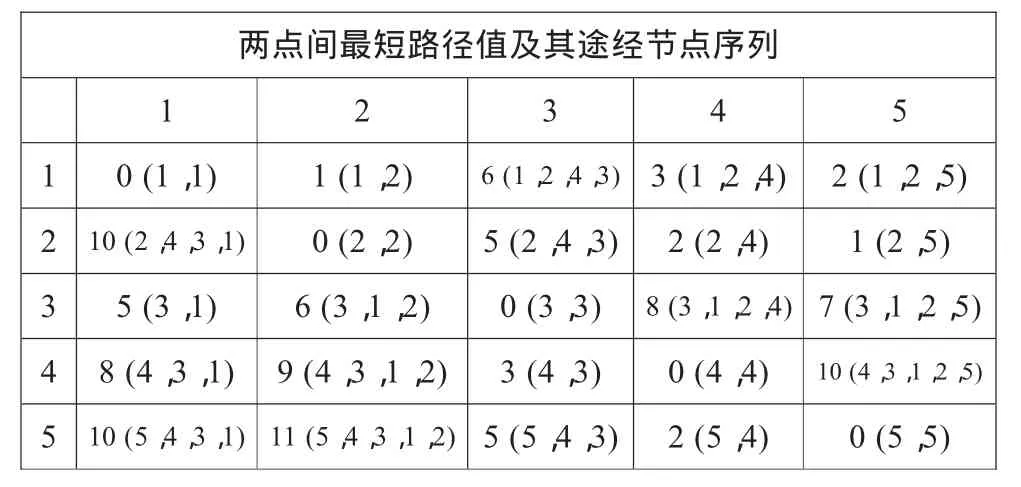
表3 第二次迭代后结果

第二次迭代的结果是两个节点之间最多跨接3个节点（如表3所示）。

(5)第三次迭代

第三次迭代的结果是两个节点之间最多跨接5个节点。在本例中本次迭代与上次结果相同（如表3所示），此矩阵内存储的数据即为最终结果，迭代过程就此结束。

2.1.2 Floyed算法

具体算法描述：

Floyed算法的目的是求出具有n个节点的图中每一对节点之间的最短路径。算法思想是：

假设求节点vi到vj的最短路径。如果从vi到vj有弧，则从vi到vj存在一条长度为cost[i，j]的路径，该路径不一定是最短路径，尚需进行n次试探。

首先考虑路径(vi，v1，vj)是否存在（即判别弧(vi，v1)和(v1，vi)是否存在）。如果存在，则比较(vi，vj)和(vi，v1，vj)的路径长度取长度，较短者为从vi到vj的中间节点的序号不大于1的最短路径。

在此基础上再考虑增加一个节点v2，也就是说，如果（vi，…，v2）和（v2，…vj）分别是当前找到的中间节点的序号不大于1的最短路径，那么（vi，…，v2，…vj）就有可能是从vi到vj的中间顶点的序号不大于2的最短路径。将vi与vj之间所有中间节点的序号不大于2的最短路径和中间节点的序号不大于1的最短路径进行比较，选出最短的路径，从而得到中间节点序号不大于2的最短路径。

在此基础上再考虑增加一个节点v3，继续进行试探，从而得到vi与vj之间的中间节点序号不大于2的最短路径。

以此类推，直到增加最后一个节点，找到vi与vj之间的中间节点序号不大于n的最短路径。

按此方法，可以同时求得各对节点间的最短路径。

现通过一个实例结合本人用此算法的编制的程序说明其处理过程。此算法本应三重循环一气呵成，但是为了演示并说明处理过程，特在程序中设置了间断点，以方便理解算法的原理。

演示步骤（篇幅所限，用图表表示）：

(1)输入两点之间的权值（距离）（见图1）；

(2)生成邻接矩阵（见图2）；

(3)处理序号为1的节点，结果如表5所示。

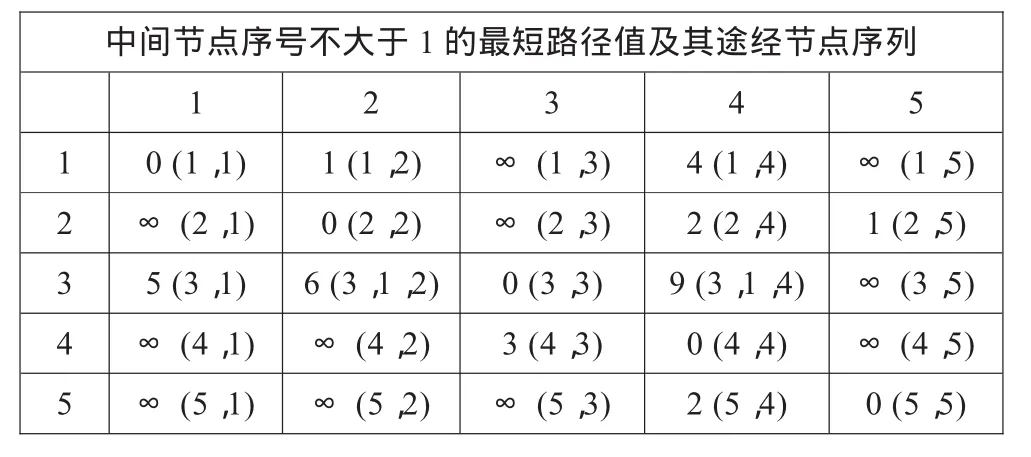
表5 Floyed算法处理序号为1的节点结果

（4）依次处理序号为2、3、4、5的节点。由于篇幅所限，仅列出5号节点处理后的结果如表6所示。

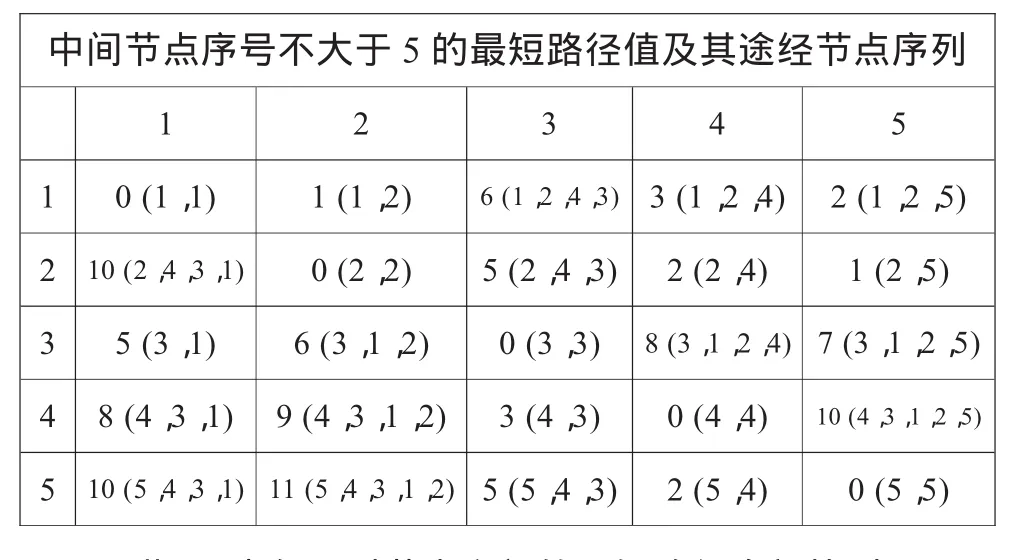
表6 Floyed算法处理序号为5的节点结果

至此，图中每一对节点之间的最短路径全部找到。

2.2 两种算法的联系与区别研究

(1)两种算法的相同点

两种算法均采用邻接矩阵的方式来存储原始权值、中间结果及最终结果，在寻找最短路径的过程中都采用对矩阵内数据元素进行算术及逻辑运算，从跨接1个节点的路径开始逐步扩展，最终得到所有结点之间最短路径的结果，两种算法的时间复杂度均为O(n3)

(2)两种算法的处理方法不同

矩阵算法在寻找最短路径过程中采用逐步迭代的方式进行，每次迭代可以找到任意两点间跨接的节点个数在限定范围内的最短路径。通过每次迭代最多跨接2k-1个节点（其中k为迭代的次数）的递增顺序，逐步求得两点之间的最短路径。这种算法在迭代的过程中不强调节点的顺序，而主要把精力聚焦在跨接节点的个数上，随着迭代次数的增加，跨接的节点数随之增加，直到跨接的节点数达到可能的最大值，至此最短路径全部找到。

Floyed算法在寻找最短路径的过程中采用三重循环的方式进行，运算过程依赖于节点的序号，即先计算跨接1号节点的所有当前最短路径，再在此基础上查询跨接2号节点的当前最短路径，以此类推，最终找到跨接最后一个节点的最短路径，至此找到所有最短路径结果。

两种算法虽然处理方式不同，但实践证明都是科学有效的方法。

(3)探讨两种算法的附加功能

根据上述的分析可见，矩阵算法在寻找最短路径过程中，第k次迭代的结果是得到最多跨接2k-1个节点（其中k为迭代的第次数）的最短路径，逐步迭代后最终求所有节点间的最短路径。这样做的好处是处理过程清晰明确，而且具有实用价值。例如：在公交运行查询中，乘客可以找到最多换乘n次车的最短路径。对于乘客来说，两地之间的最短路径并不意味着最方便，顾客往往希望尽量少换车次但路径尽可能短的情况。例如从A地到B地有几种走法，第一种走法是只乘1辆车即可到达终点，汽车共行驶20km；第二种走法是中途换乘1次车，汽车最短行使15km；第三种走法是中途换乘3次车，汽车最短行驶12km。年老体弱的人可能选择第一种方法，年轻人可能选择第二或第三种方法。因为换乘次数少而且距离相对较短，所以大多数人会舍弃距离更短的第三种走法而选择第二种走法。运用矩阵算法可以通过逐次迭代过程的中间结果告知乘客换乘的次数及相应的最短路径，以此方便乘客在乘车距离与换乘次数之间进行平衡。又例如在货物运输过程中，运输公司往往要在时间与距离两个方面寻找平衡点，有些路段虽然距离近但路面质量低或道路拥堵造成耗时多，而有些路段虽然距离远但行驶顺畅耗时少，针对这种情况，矩阵算法可以向运输公司提供多种路径选择方式，以更为人性化的方式提供交通信息服务。

Floyed算法在寻找最短路径的过程中采用三重循环的方式进行，运算过程依赖于节点的序号。这种方法程序实现起来容易，但是处理过程相对来讲没有运筹学的矩阵算法清晰，中间处理结果没有什么实用价值，因而几乎没有可以应用的附加功能。

(4)矩阵算法在数学解释方面有助于对Floyed算法的理解

矩阵算法采用数学中矩阵运算的方式进行最短路径的查找，逻辑清晰、推理严密，使人一目了然。

Floyed算法采用三重循环结构逐个节点递进的方式完成最短路径的查找，虽然在数学方法的支撑与论证方面有些欠缺，但通过对实际问题的分析与逻辑判断，迄今为止此算法仍然是科学有效的经典算法。同时，矩阵算法在数学解释方面有助于加深对Floyed算法的理解。

总之，最短路径问题可以采用不同的算法来解决，这些算法各有区别、各具千秋，在实际应用的过程中要结合需求选择恰当的算法，以求实用、高效、快捷。

[1] 严蔚敏，吴伟民.数据结构[M].北京：清华大学出版社，1987.

[2] 胡运权.运筹学基础及其应用[M].北京：高教出版社，2004.

[3] 张炯民，窦亮，黄国兴.数据结构与算法教程[M].上海：华东师范大学出版社，2007.

[4] 胡运权，郭耀煌.运筹学教程[M].北京：清华大学出版社，2007.