混合跨导线性回路在电流控制传送器的运用

李亨王丽萍王明磊曹元伟

(1.机械工业第六设计研究院，河南郑州450007；2.河南科技大学电子信息工程学院，河南洛阳471003）

1.引言

CCII问世后由于其X端有一个寄生电阻（约为几十欧至一百多欧），导致了基于CCII的传输函数出现误差。针对此缺陷，1995年法国学者Fabre等人利用双极型晶体管的线性互导（translinear loop）特性实现了第二代电流控制传送器CCCII(Second Generation Current Controlled Conveyor)[1]，从而使电流传送器的应用扩展到了电调谐功能领域。

2.电流控制传送器（CCCII）

CCCII是从CCII改进而来的，从表达式（1）可以看出其输入与输出特性与CCII的输入与输出特性类似。但内部其实多了一个可调电阻Rx，这一特性使CCCII有了与OTA相同的特性即元件本身自行产生一电阻效应，使设计者在设计电路时可以减少无源元件的使用。其思想是利用X端寄生电阻的大小是由电流传送器内部偏置电流决定这一原理，使用一内部直流IO偏压控制X端寄生电阻，达到电子可调的特性。CCCII对应的元件符号如图1。CCCII各端对应的关系式为：

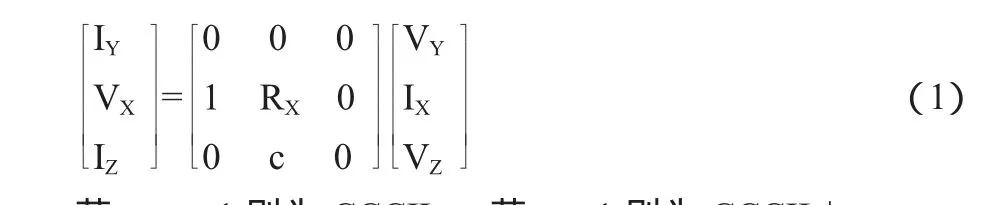
若c＝－1则为CCCII－，若c=+1则为CCCII＋。

X端寄生电阻即为Rx，其值可通过偏置电流IO进行调整，其具体的的对应关系如式（2），其中VT是热电压。

图1 电流控制传送器

从输入输出特性来说Y端是没有电流流入，X端与Y端的电压是相互追踪的，而X端的电压较Y端大了IxRx，X端与Z端的电流是相等。可以认为CCCII是在理想的CCII的基础上通过在X端连接一可调电阻Rx实现的，其等效模型如图1(b）。

3.跨导线性回路

3.1 跨导线性电路回路

跨导线性电路是接近真正电流模式工作的电路。事实上IC和VBE之间的关系正是双极型晶体三极管(BJT)的核心所在。晶体管由电压VBE驱动下，产生集电极电流IC，表示为IC=ISexp（VBE/VT）进而可以得到跨导gm=d IC/dVBE=IC/VT，所以理想BJT的跨导gm与其集电极静态电流IC呈线性正比例关系。具有跨导线特性的电路称为跨导线性电路。

3.2 跨导线性回路

跨导线性回路原理可表述为：在一个包含偶数个正向偏置结的闭环中，若将结排列成面向顺时针方向和面向逆时针方向，其极性、数目相等，则顺时针方向的电流密度积等于逆时针方向的电流密度积。

该原理的证明如下：

晶体管的集电极电流IC=ISexp（VBE/VT）（热电势VT=kT/q，IS为晶体管的饱和电流或反向饱和电流），ISi=ASiJS（iJSi为饱和电流密度，Ai为发射区面积）对于单片集成电路来说，可认为JSi都相同，故因为跨导线性环内的结数必须是偶数（至少两个），而且面向顺时钟方向（CW）和面向逆时钟方向（CCW）的结数相等。按顺时针方向（CW）与逆时针方向（CCW）方向分类，则顺时针方向的PN结压降之和与逆时针方向PN结压降之和相等，即：称为面积因子，则可得到：

在跨导线性回路中，器件对之间的发射区面积之比很重要。在设计电路时，通过精心设定对管发射面积之比，可获得预期的电路性能和效果，有助于减小乃至消除由于结电阻产生的误差。

图2 跨导线形回路

如图2(a)所示为一跨导线形回路，其含有n=4个BJT发射结（PN结）的跨导线性回路原理电路。设每个发射结均被偏置到正向工作状态，且面积相同。则根据跨导线性可得I1I2=I3I4。这就是一个TL方程，是静态电子方程的一个基础式。使用三极管替代二极管时要使VCB=0，这样当晶体管面积相同时，则可得：

3.3 混合跨导线性回路的实现

传统的CCII在其X端间存在寄生电阻（约为几十欧至一百多欧）而传输特性并没有考虑这个电阻，使得X与Y端的电压跟随无法达到理想要求，这就导致了基于CCII的传输函数出现误差。归结到一点，整个电路的设计就在于如何减小电压跟随器的误差，使之得到理想的传输函数。

3.3.1 混合跨导线性回路

1991年，Alami和Fabre提出了跨导线性（Translinear）电流传送器的实现电路[2]。1992年，Fabre和Houle提出了另一种跨导线性电流传送器（CCII+）实现电路[3]，跨导线性回路是CCII乃至CCCII中最为关键的基本单元之一，CCCII的特点也是由跨导线性回路的特性所决定的。

而对应的图2(b)中Q1与Q2构成了跨导线性回路，而Q3与Q4使得Q1要满足ICB1=0这个必要条件来提高电流传输的精度。电流的输入输出比IS/IE推导如下：令Q1、Q2、Q3、Q4的放大倍数都为β，且β>>1。根据图2(b)原理有I1C=I3E，根据跨导原理可得I2C=I1C而I2C=βI4E/(β+2)故可得I3E=βI4E/(β+2)。

3.3.2 混合跨导线性回路实现电压跟随器

图中2(c)使用的为PNP与NPN混合跨导线性回路，当存在其它的电路使得Q2和Q4的CB端电压为0V。易知当每个管β>>1时，利用跨导线性回路有可得到I1I3=I2I4，I3=I1+IA，I4=I2+IB以及I为对称的值。且根据其对称性可知：VA≈VB

4.基于跨导线性回路的CCCII实现

4.1 基于跨导线性回路的CCCII实现

Alain Febra等人设计出的基于双极管跨导线性回路的正电流控制传送器的电路实现原理（如图3(b)所示），正是使用了图3(a)所使用的的混合跨导线性回路实现的电压跟随器电路。

如图3(a)通过加载两个相同的偏置电流源，使得在β＞＞1时有I1=I3≈IO。这时输入端A呈现高阻态，输出端B呈现低阻态，此时电路为一电压跟随器。下面计算A、B间的电压。A、B端的电压差由电流ix的大小决定可表示成VBA=VBE1－对于单片集成电路来说，可认为JSi都相同，Ai都相同。则可得到

而对于图3(a)，有IC1就是I1，IC2就是I2，故有IC1≈IO，代入后即得：

在27℃时算式中的热电压VT=kT/q≈26mV，而对应I2和I4当IO＞＞IX可得

图3 混合跨导线性回路

假设IX的幅值远小于2I0的幅值时则有：

由式（11）明显可见等效电压跟随器的小信号输出阻抗为Rx=VT/(2IO)，可以通过调节回路的偏置电流IO来控制Rx。

这样CCII原来的传输函数中电压的误差在CCCII中可以通过改变直流偏置电流实现控制和调节，在设计电路时只要给予充分合理考虑即可。混合跨导线性回路Q9和Q10以及Q11至Q13分别组成了两个镜像电流源，提供电路所需的两个直流偏置电流源IO。而Z端则可使用传统的方法，通过两个互补的电流镜实现对X端电流的复制，如图3(b)。

4.2 基于双极管的负寄生电阻CCCII的实现

一般我们遇见的CCCII电路的X端寄生电阻Rx为正值即Rx＞0。2002年Alain Fabre等人提出了寄生电阻为负即Rx＜0的电流控制传送器，其电路原理如图4。

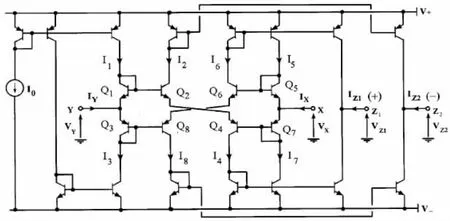
图4 负寄生电阻CCCII原理图

Q1至Q8组成跨导线性回路，通过两个互补的镜像电流源使得I5=I6和I4=I7。而且直流电源IO提供给以二极管形式出现的Q1和Q3偏置电流，显然I1=I3=IO。假设都为理想晶体管并完全匹配，而且β＞＞1。如图4所示，由于晶体管Q2和Q4以及Q6和Q8的分别发射极相连I6=I8和I2=I4。Q1至Q8组成一个混合跨导线性回路，可得：I1I3I5I7=I2I4I6I8。

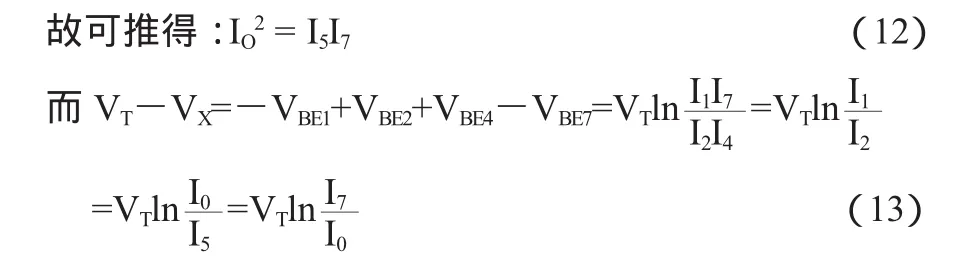
假设IX的幅值远小于2I0的幅值时，有：

可见等效电压跟随器的小信号输出阻抗为负值Rx=-VT/(2IO)。显然，可以通过调节回路的偏置电流IO来控制Rx。

5.结论

电流控制传送器作为电流传送器的改进，通过内部使用混合跨导线形回路的电压跟随器，利用了跨导回路的性质，实现了对X端寄生电阻的可调节的性质。对比传统的电流传送器，有了更多的场合，有了更加灵活的设计方法。

[1] Alain Fabre，Omar Saaid，Christophe Boucheron.Current controlled bandpass filter based on translinear conveyors.Electronics Letters，1995，31(20)：1727-1728.

[2] Alami M，Fabre A.Insensitive current mode bandpass filter implemented from two current conveyors.Electronics Letters，1991，27(5)：897-899.

[3] Fabre A，Houle JL.Voltage-mode and current-mode Sallen-Key implementations based on translinear conveyors.In：IEE Proceedings-G，1992，139(4)：491-497.