基于第一性原理的KMgF3晶体电子结构和光学性质研究

程 芳, 刘廷禹, 张启仁, 乔海玲, 周秀文

(上海理工大学理学院,上海 200093)

KMgF3晶体是无色透明的氟化物,由于其结构简单、对称性高且具有良好的光学均匀性和热稳定性、熔点低、光学透过率高、容易实现不同价态稀土离子的掺杂,因而KMgF3是探寻新型激光材料的理想基质[1].同时,KMgF3单晶在高能辐照下具有交叉发光性能[2-3],发光在紫外区,衰变时间大约为1 ns,因此可作为快速闪烁体材料用来检测高能粒子[4-5].KMgF3单晶在紫外波段具有很高的透过率,是很有潜力的窗口材料[6].目前对掺杂的KMgF3离子晶体性质研究已有大量的报道[7-9],但对纯的KMgF3单晶的研究还很少,到目前为止,尚无KMgF3晶体电子结构和光学性质的第一性原理计算的研究.而利用CASTEP研究晶体的电子结构和光学性质已经有很多成功的例子[10,11],因此,本文利用CASTEP软件系统地对完整KMgF3晶体的光学性质进行了模拟计算.以期揭示KMgF3离子晶体的光学性质与晶体的电子结构以及晶体结构之间的关系,并为研究含缺陷的KMgF3离子晶体的光学性质打下基础.

1 晶体结构和计算方法

1.1 晶体结构

KMgF3晶体为典型立方钙钛矿型结构复合氟化物,晶格常数为0.397 3 nm,空间群为O1h(Pm3m).如图1所示,单位晶胞含有一个KMgF3分子.氟原子的点对称性为D4h,Mg和K原子是Oh.K离子占据立方体的顶角,Mg离子在立方体体心,F离子在6个面的面心.本文计算选用一个以Mg为中心,包含8个K、8个Mg和24个F的团簇进行模拟计算.

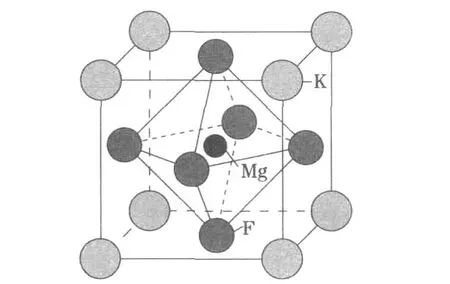
图1 KMgF3晶体结构示意图Fig.1 Cubic(O1h)lattice structure of KMgF3

1.2 计算方法

利用商业材料模拟计算软件CAST EP,计算过程选用超软赝势(ultrasoft pseudopotential)描述价电子与芯态的关系,结构优化计算基于局域密度泛函理论框架下的广义梯度近似平面波超软赝势方法,交换相关势采用PW91,钾、镁和氟的平面波剪断能量为340 eV.结构优化的收敛条件为:a.每个原子的最大的能量变化小于10-5eV;b.原子的最大位移小于10-4eV;c.每个原子受到的最大作用力小于0.5 eV/nm.从而得到几何优化及稳定的晶格结构.

密度泛函的基本理论是解Kohn-sham方程.介电常数是一个二阶张量,并且其虚部直接与固体的能带结构相关联.在Koopmans近似(不考虑电子极化效应的单电子紧带近似)和可见及近紫外线性光学条件下,介电常数虚部可为[12-13]

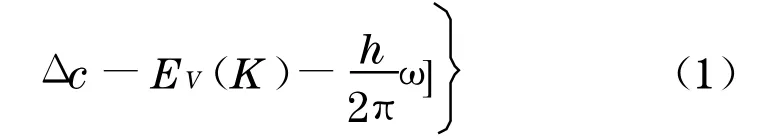
式中,e为电子电量;ε0为真空中的介电常数;m为自由电子的质量;ω为入射光子的频率;Δ c为剪刀算子值的偏移量;EC、EV为导带和价带的能量;h为普朗克常数;K为波矢;α为矢量势A的单位方向矢量;MV,C为偶极跃迁矩阵;BZ为布里渊区.介电函数的实部εr(ω)根据Kramers-Kronig(KK)变换关系[12]得到.由于采用密度泛函理论计算得到的固体能带的禁带宽度总是偏小的,因此采用剪刀算子进行修正.根据完整的KMgF3晶体的计算结果(禁带宽度为7.6 eV)与试验(12.4 eV)的偏差,剪刀算子值取为4.8 eV.展宽因子取为0.12 eV.对布里渊区积分选取了14个独立的k点.介电函数的实部根据Kramers-Kronig变换关系计算得到.利用折射率、吸收系数、吸收光谱等与介电函数的关系以及KK变换关系,可以求出各自的函数.关于使用CASTEP方法的详细介绍参见文献[14-15].

2 计算结果及分析

2.1 电子态密度分布图

通过用自洽迭代方法求解Kohn-Sham方程,得到基态的能量和体系处于基态的波函数,从而可得到晶体的能带结构和总电子态密度.计算得到的电子态密度分布如图2所示.从电子态密度分布曲线可以看出,a.完整的KMgF3晶体的禁带宽度为12.4 eV;b.价带顶主要由氟的2p态组成,在价带中有5个态密度峰值位置,它们分别处于-2.8,-1. 7,-1.4,-0.9和-0.5 eV,F2p态的宽度约为4. 25 eV,F 2p与K3p态之间的能量差值约为8 eV; c.导带底主要由3种原子的s态组成,宽度约为4.3 eV,在导带中有6个态密度峰值位置,它们分别处于12.9,13.3,13.7,14.4,15.7和16.4 eV.该计算结果与相关文献[16-18]报道的结果吻合得较好,这说明在此基础上所作的进一步计算是有依据的.

2.2 介电函数的虚部

利用介电函数与能带之间的关系,计算得到介电函数的虚部随人射光频率的关系,如图3所示.从结果上看,在能量小于19 eV的范围内出现8个介电函数峰值,它们的位置分别为12.7,13.3,13.7, 14.0,14.9,16.4,16.7,17.5 eV;能量大于19 eV的范围内主要出现7个小的峰值,它们分别位于19.6, 21.9,22.4,22.7,23.5,24.4,25.4 eV.利用复介电函数实部与虚部的KK关系

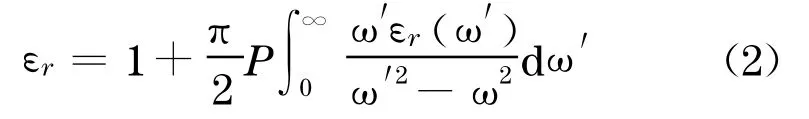
式中,P为科西积分的主值,可求得的介电函数的实部,如图3中虚线所示.

图2 计算得到的KMgF3的总态密度和分态密度Fig.2 Calculated total and partial density of states(DOS)for KMgF3

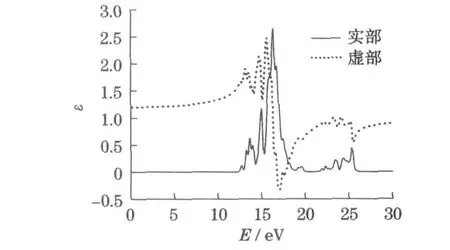
图3 KMgF3晶体偏振光的复数介电函数的实部和虚部Fig.3 Real part and imaginary part of the complex dielectric function for polarized light in the KMgF3crystal

2.3 吸收光谱

利用介电函数与吸收系数之间的关系,计算得到吸收系数

式中,εim为介电常常;n为折射率;c为光速;ω为圆频率.计算结果如图4所示.其吸收峰位置与介电函数的虚部的峰值位置十分接近,但两者的强度分布相差较大.吸收光谱的最强吸收峰位于16.7 eV.比较电子态密度分布图和吸收光谱的峰值位置发现: a.电子从价带中分别处于5个峰值位置跃迁到导带中的峰值位置,即F 2p→K 4s,其对应的跃迁能量(峰值位置能量的差)分别为13.3,13.7,14.7,16. 1,17.2 eV,其结果与能量小于19 eV范围内的吸收光谱的5个峰值位置(12.7,13.7,15.0,16.4,16.7 eV)比较接近,但存在一定的偏差,这种偏差存在的主要原因可能是电子吸收跃迁能量应考虑电子跃迁过程中发生的驰豫效应,而不是简单的两个能级差; b.K 3p→Mg 3 s跃迁对应的能量分别为21.9,22. 3,23.3,24.3,24.7 eV,其结果与吸收光谱的6个峰值位置(21.9,22.4,23.5,24.4,25.4 eV)比较接近; c.能量大于26 eV的吸收光谱的2个小峰(35.0, 41.2 eV),可能分别与F 2s→K 4s,K 2s→Mg 3s跃迁有关;d.完整的KMgF3晶体在可见光范围内没有吸收,所以KMgF3晶体应该是一种透明的晶体. T.Fukuda等人[19]在实验中观察到KMgF3晶体的透过率光谱在110 nm(13.6 eV)处开始显著减少,而计算结果表明,KMgF3晶体从13.7eV开始出现显著的吸收,两者变化趋势相同,计算结果与实验报道的结果相吻合.

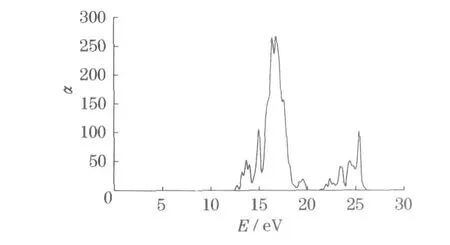
图4 KMgF3晶体的吸收光谱Fig.4 Absorption spectrum of the perfect KMgF3crystal

2.4 复数折射率和复数光电导谱

根据复数折射率与复数介电函数的关系

可以导出折射率n和消光系数κ,其中,εr为介电函数的实部.计算结果如图5所示(见下页).n在能量小于19 eV的范围内出现8个峰值(它们的位置分别为12.7,13.3,13.7,14.0,15.0,16.4,16.8,17.5 eV);能量大于19 eV的范围内主要出现7个小的峰值(它们分别位于19.6,21.9,22.4,22.7,23.5, 24.4,25.4 eV).其峰值位置与介电函数的虚部的峰值位置接近.

根据光电导的实部与介电函数的虚部的关系

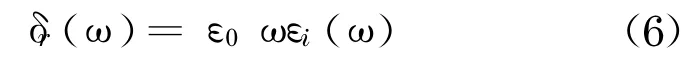
式中,δr为光电导实部;ε0为真空介电常数;εi为介电函数的虚部.

计算得到的光电导如图6所示.光电导的实部在能量小于19 eV的范围内出现8个峰值,它们的位置分别为12.7,13.3,13.7,14.0,15.0,16.4,16.7,17.5 eV;在能量大于19 eV的范围内主要出现7个小的峰值,它们分别位于19.6,21.9,22.4,22.7,23.5,24.4, 25.4 eV.光电导的实部计算结果显示其峰值位置以及强度都与介电函数的虚部十分近似.

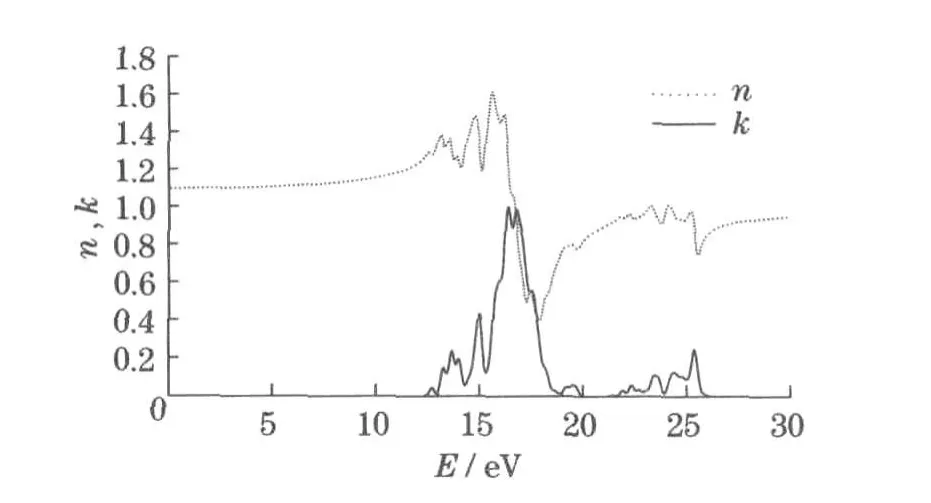
图5 KMgF3晶体的复数折射率Fig.5 Complexrefractive indexof the perfect KMgF3single crystal

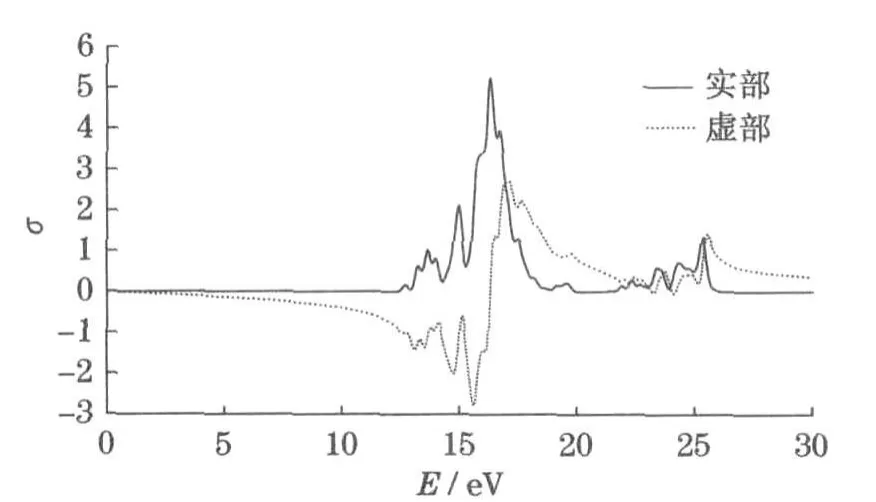
图6 KMgF3晶体的光电导Fig.6 Conductivity of the perfect KMgF3single crystal

综上所述,介电函数的虚部、吸收光谱、复折射率和复数光电导谱的峰值位置十分接近,说明它们存在着内在的联系,都与电子态密度分布直接相关.

3 结 论

采用第一性原理的 CASTEP计算了完整KMgF3晶体的电子结构和介电函数,分析了完整的KMgF3晶体可能的跃迁及其对应的吸收光谱,并利用KK关系导出完整的KMgF3晶体的复数折射率和复数光电导谱.结果表明,吸收光谱与电子从价带到导带的跃迁(F 2p→K 4s,K 3p→Mg 3s,F 2s→ K 4s,K 2s→Mg 3s)有关;完整KMgF3晶体在可见光范围内没有吸收,所以完整KMgF3晶体是无色透明的晶体;介电函数的虚部、吸收光谱、复折射率和复数光电导谱的峰值位置存在一一对应关系,说明它们之间存在着内在的联系,这些都与电子态密度分布直接相关.计算结果与实验值基本相符,为进一步研究含缺陷及掺杂的KMgF3晶体的光学性质提供理论基础.

[1] SHKADAREVICH A P,DUBINSKII MA,NIKANOVICH M V,et a1.Tunable room temperature laser on color centers in KMgF3[J].Optics Communications,1986,57:400-402.

[2] GEKTIN A V,KOM AR V,SHIRAN N V,et al.Radiation damage of pure and doped KM gF3crystal [J].IEEE Trans Nucl Sci,1995,42:311-314.

[3] JANSONS J L,KRUMINS V J,RACHKO Z A,et al. Crossluminescence of KF and related compounds[J]. Solid State Communications,1988,67:183-185.

[4] BUSULUTSKOV A E,BRITVICH G I,KOCHETKOV V I,et al.Study of the KMgF3scintillator radiation damage[J].Nuclear Instruments and Methodsin Physics Research Section A,1992,322:235-238.

[5] SHIRAN N V,GEKUELE A V,KOMASUM V K,et al.Thermoluminescence of KMgF3(RE)crystals [J].Radiation Measurements,1995,24:435-437.

[6] SATO H,BENSALAH A,SOLOVIEVA N.et al.X-ray damage characterization in BaLiF3,KMgF3and LiCaAlF6complex fluorides[J].Radiation Measurements,2004,38:463-466.

[7] SHIRAN N V,KOMAR V K,SHLYAKHTU ROV V V,et al.Radiation effects in pure and RE doped KM gF3[J].Radiation Effects and Defects in Solids, 1995,136:197-200.

[8] GEKTIN A V.SCINTILLATORS and storage phosphors based on ABX3crystals[J].Journal of Luminescence,2000,87-89:1 283-1 285.

[9] SEO H J,MOON B K,TSUBOI T.Two-photon excitation spectroscopy of 4f7→4f7transitions of Eu2+ions doped in a KMgF3 crystal[J].Phys Rev(B), 2000,62:12 688-12 695.

[10] LIU T Y,ZHANG Qi-ren,ZHUANG Song-lin.First principle studies on the electronic structures and absorption spectra under polarized light for the PbWO4crystal with oxygen vacancy[J].Solid State Communications,2004,132:169-173.

[11] LIU T Y,ZHANG Qi-ren,ZHUANG Song-lin.Firstprinciples study on the electronic structures and absorption spectra for the PbWO4crystal with lead vacancy[J].Solid State Communications,2005,135: 382-385.

[12] 方容川.固体光谱学[M].合肥:中国科学技术大学出版社,2001.

[13] ABRAHAM Y,HOLZWARTH N,WILLIAMS R.Electronic structure and optical properties of CdMoO4and CdWO4[J].Phys Rev(B),2000,62:1 733-1 741.

[14] SEGALL M,LINDAN P,PROBERT M,et al.Firstprinciples simulation:ideas,illustrations and the CASTEP code[J].J Phys:Condens Matter,2002, 14:2 717-2 744.

[15] CLARK S J,SEGALL M,Pickard C,et al.First principles methods using CASTEP[J].Zeitschrift für Kristallographie,2005,220:567-570.

[16] DANIELS R R,MARGARITONDO G,HEATON R A, et al.Experimental study of the electronic structure of KMgF3[J].Phys Rev(B)1983,27:3 878-3 880.

[17] NISHIMATSU T,TERAKUBO N,MIZUSEKI H,et al. Band structures of perovskite-like fluorides for vacuumultraviolet-transparent lens materials[J].Japanese Journal of Applied Physics,2002,41:L 365-L 367.

[18] SAHNOUN M,ZBIRI M,DAUL C,et al.Full potential calculation of structural,electronic and optical properties of KMgF3[J].Materials Chemistry and Physics,2005,91:185-191.

[19] FUKUDA T,SHIM AM URA K,YOSHIKAWA A,et al.Crystal growth of new functional materials for electro-optical applications[J].Opto-electronics Review,2001,9(2):109-116.