概率论教学中的几个问题

李天则

（常熟理工学院数学与统计学院，江苏常熟 215500）

概率论教学中的几个问题

李天则

（常熟理工学院数学与统计学院，江苏常熟 215500）

讨论了概率论教学中几个应该注意的问题，分析了国内概率论教材中中心极限定理部分存在的一个问题。

可列可加性；随机变量；离散；连续；中心极限定理

概率论中有一些概念比较容易混淆和难以理解，初学者学习起来有些困难，往往抓不住实质，理解不透彻。为此，我们给出一些简单有趣的例子，以利于初学者深入理解教材内容。

一、怎样理解概率的可列可加性

概率是随机事件发生的可能性大小，这是概率的描述性定义。为了给出概率的严格数学定义，历史上先后出现了古典定义、几何定义、统计定义。但是这几个定义要么适用范围有限，要么在数学上并不严格。直到1933年前苏联数学家柯尔莫哥洛夫提出了概率的公理化定义，才使概率论成为一个严谨的数学分支。

要完整地描述概率的公理化定义需要测度论的语言，目前国内非数学专业的概率论教材中关于概率的定义大多采用经过简化处理的公理化定义［1］。概率的公理化定义中很关键的一点是可列可加性。初学者很容易接受有限可加性，但对于可列可加性往往感到很迷惑。下面是几何概型的一个例子，有助于理解概率的可列可加性。

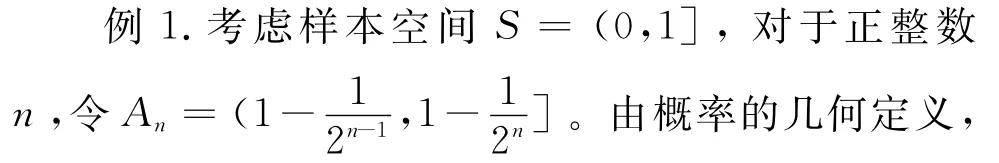
这就解释了概率的公理化定义中为什么要规定可列可加性．

二、关于概率可列可加性的思考

正是由于引进了可列可加性，概率论才能够使用数学的其它分支包括测度论的工具和成果，从而得到迅速的发展。但是概率真的是可列可加的吗？概率的公理化定义能够处理所有的概率问题吗？事实上可列可加性排斥了一些有趣的例子。

例2.在自然数集中任意取一数，问恰好取到数1的概率是多少？

本例中样本空间S是自然数集。显然恰好取到数1和其余各数的概率都相同，记为p。我们断言p只能等于0。否则取S的一个有限子集A，使其元素个数n满足n p＞1。于是，由有限可加性得到P（A）=n p＞1，与P（A）≤1矛盾。然而由p=0及可列可加性，我们又得到P（S）=0，与P（S）=1矛盾。

上述例子说明了在柯尔莫哥洛夫的公理化定义框架下，可列样本空间中不存在样本点为等可能的概率模型。

三、概率为0的事件

由概率的定义，不可能事件的概率为0，但概率为0的事件不一定是不可能事件。类似地，必然事件的概率为1，但概率为1的事件不一定是必然事件。这也是初学者容易迷惑的地方。教材中一般会证明这样一个结论：设X是连续型随机变量，a是任意实数，那么概率P（X=a）=0。这就解释了上述事实。但是这比较抽象，下面我们再给出一个具体的、有生活背景的例子。

例3.甲、乙二人约定1点到2点之间在某处碰头，假设甲、乙二人各自随意地在1-2点之间选一个时刻到达该处。问甲乙二人在同一时刻到达该处的概率是多少？

本例属于几何概型，样本空间可取为S= （x，y）|0＜x，y＜｝

｛1，所求事件为A=“甲、

乙二人在同一时刻到达该处”= （x，y）|x=y，0＜x，y＜｝

｛1。由于线段的面积为0，故事件A的概率P（A）=0。

从随机变量的观点看，我们可以定义Z：S→R为Z（（x，y））=x—y。即Z是甲、乙二人分别到达该处的时刻差。显然｛Z=0｝就是事件A，所以P（Z=0）=P（A）=0。

上述例子说明了概率为0的事件也有可能发生。一般称概率为0的事件为几乎不可能事件，而概率为1的事件为几乎必然事件。

有趣的是上述随机变量Z服从辛普森分布（或三角分布）［2］。

事实上Z是连续型随机变量，其分布函数为

四、既非离散又非连续的随机变量

教材中一般会提到除了离散分布和连续分布之外，还有既非离散又非连续的分布。但初学者往往对此印象不深，因为教材中的例题一般只讨论离散分布和连续分布。请看下面的例子［2］。

由分布函数的三个判别条件（单调性、有界性和右连续性），易知F（x）确是某个随机变量X的分布函数。因为F（x）既不是阶梯函数，又不是连续函数，所以X是既非离散又非连续的随机变量。

美中不足的是我们不知道F（x）所对应的随机变量X是什么。下面的例子可以说明X是怎样产生的。

例5.设有一个周长为2的均匀陀螺，在其圆周的半圆上都标明刻度0，另外半圆上均匀刻上区间（0，1］上诸数字，旋转这陀螺，求它停下来时其圆周上触及桌面上点的刻度X的分布函数。

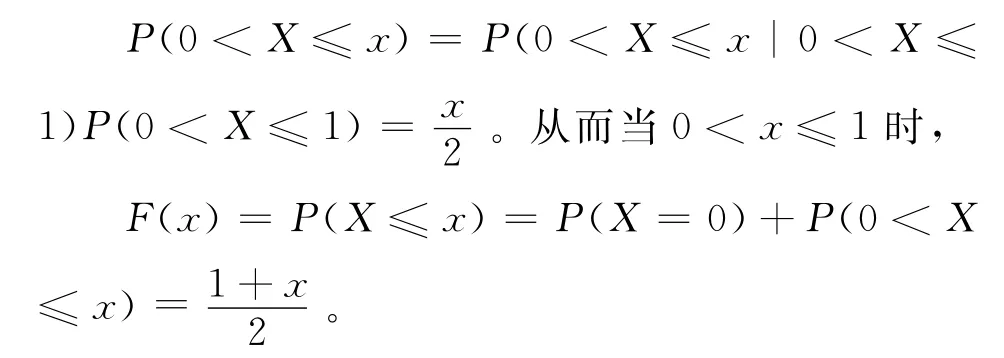
因此，随机变量X的分布函数确实是例4中的F（x）。

五、中心极限定理教学中的一个问题

下面是中心极限定理的一个典型例子．

例6.某系统由100个相互独立的部件组成，在运行期间每个部件损坏的概率均为0.1，为使系统正常工作，必须至少有88个部件正常，求整个系统在运行期间能正常工作的概率。

很多教材会给出“标准”解法如下：

解法一：考虑第i个部件，引入随机变量Xi，若第i个部件损坏，则令Xi取值为0，否则令Xi取值为1，从而根据棣莫弗—拉普拉斯极限定理知所求概率为

注意到二项分布是离散分布，而正态分布是连续分布，所以在用正态分布作为二项分布的近似计算时，通常要做一个“连续性修正”［2，4，5］以提高精度。具体说就是：若k1＜k2均为整数，一般先作如下修正后再用正态近似

P（k1≤X≤k2）=P（k1—0.5≤X≤k2+0.5）。

按照“连续性修正”方法，上述两个解法将会统一起来，我们考虑一般的情形。

例7.设X～b（n，p），其中n＞＞1，0＜p＜1，另外，k是一个自然数且1＜k＜n，试用中心极限定理估算概率P（X≥k）。

解法一：

将n=1 0 0，p=0.9，k=8 8代入上述结果，知例6中所求概率约为1—Φ（—0.8 3 3）=0.7 9 6 7。显然这个结果较前面两个解法的结果精度要高不少。仔细分析以上三种计算方法可以发现，当n足够大时，三种结果将会相差很小，此时用哪一种方法都可以。但是当n不太大时，还是采用“连续性修正”方法为好。

［1］盛骤，谢式千，潘承毅，等.概率论与数理统计［M］.北京:高等教育出版社，2008．

［2］茆诗松，程依明，濮晓龙，等.概率论与数理统计教程［M］.北京:高等教育出版社，2004：69-70．

［3］翟桥柱.中心极限定理教学中的一个问题［J］.大学数学，2004（4）：125-126．

［4］陈希孺.概率论与数理统计［M］.合肥：中国科学技术大学出版社，2009．

［5］Ross S M.概率论基础教程［M］.郑忠国，詹从赞，译.北京:人民邮电出版社，2010．

Some Problems in the Teaching of Probability Theory

LI Tian-ze
(School of Mathematics and Statistics,Changshu Institute of Technology,Changshu 215500,China)

Some concepts in probability theory and a problem in the teaching of central limit theorem are discussed in this paper．

countable additivity;random variable;discrete;continuous;central limit theorem

O211

A

1008-2794（2010）12-0101-03

2010-09-06

李天则（1977—），男，福建南安人,常熟理工学院数学与统计学院讲师，博士，主要研究方向为有限群论。