光滑粒子流体动力学法拉伸不稳定性改进研究

贾 斌，马志涛，张 伟，庞宝君

(1.哈尔滨工业大学航天工程系，哈尔滨150080，jiabin@hit.edu.cn;2.清华大学航天航空学院，北京100084)

光滑粒子流体动力学(Smoothed Particle Hydrodynamics，简称SPH)法最初是由Lucy L B［1］于1977年提出的一种纯Lagrange无网格方法，并在天体物理领域里得到了广泛应用，成功地模拟了超新星爆发、银河系的形成和演化、云团的碰撞等超大尺度的复杂问题.该方法的基本思想是将整个流场的物质离散为一系列具有质量、速度和能量的“粒子”，然后通过一个称为“核函数”的积分进行“核函数估值”，从而求得流场中不同位置在不同时刻的各种动力学量.1993年Libersky L D等［2］首先将材料强度效应引入SPH方法，成功进行了高速碰撞数值模拟.

但SPH方法中存在着一些内在的缺点，其中一个主要问题便是1995年Swegle J W等人［3］指出的在具有材料强度的问题中存在着拉伸不稳定性.为改进这一问题，Morris J P［4］提出了应用特殊核函数，因为拉伸不稳定与核函数的二阶导数紧密相关，尽管此方法在一些情况中非常成功，但对于一般情况却不能总得到令人满意的结果.Wen Y等［5］及Balsara D S［6］提出了守恒光滑的方法来消除拉伸不稳定，但该方法并不能解决所有的情况，而且还增加了计算时间.Dyka C T等［7－8］首次在一维算法中引入了应力点法，随后Randles P W等［9］将该方法扩展到了多维空间，其中SPH粒子与应力粒子交错排列，该方法虽然能够解决拉伸不稳定，但增加了大量的计算时间和内存.Monaghan J J等［10－11］提出了用于稳定计算的人工力，该力与具体的核函数有关，虽然在一定程度上解决了拉伸不稳定的问题，但依然存在一定的震荡.本文提出了一种改进形式的人工力，并在人工粘性力的基础上叠加抗拉伸不稳定的人工力，建立了统一的张量形式的人工力.

1 SPH基本方程

考虑材料的弹塑性效应，全应力张量空间中的SPH插值公式的质量守恒方程、动量守恒方程、能量守恒方程分别表示为［12－13］

其中:ρ为密度;m为粒子质量;v为粒子速度;σαβ为应力张量(上角标α和β表示张量坐标);e为比内能;x为位置矢量;W为核函数;下标i为粒子编号，下标j为i粒子的近邻粒子编号.核函数取最常用的三次B-Spline函数

其中:s=|x－x'|/h，h是光滑长度;在一维、二维、三维中，αd分别为1/h，15/(7πh2)，3/(2πh3);函数的影响域|x|=2h.

2 拉伸不稳定性

2.1 压缩失稳与拉伸失稳

所谓拉伸不稳定性，是指当粒子处于拉伸应力状态时，粒子的运动变得不稳定，从而出现粒子凝集和较大的空洞.Swegle J W等［3］曾对其进行了比较细致的研究，指出这种不稳定性是由核函数的二阶导数和应力状态的乘积决定的，并提出了拉伸失稳产生的充分条件，如下式所示:

式中:W″是核函数的二阶导数.

式(4)的三次B-Spline函数曲线和一阶导数曲线如图1所示，图中s=r/h(r为粒子i和粒子j的间距)，核函数一阶导数的绝对值在s=2/3处有极大值.根据式(5)，如果核函数的二阶导数为正，则SPH方法在拉伸应力状态下是不稳定的，会出现拉伸失稳现象;反之，则是稳定的.因此，在B-Spline函数中，可以将极值点右侧的区域称为拉伸失稳区.当s＞2/3时，核函数一阶导数的绝对值随着两点距离的增大而减小，即邻近点j对计算点i的贡献随着距离的增大而减小.当s＜2/3时，核函数一阶导数的绝对值随着两点距离的减小而减小，即j对i的贡献随着距离的减小反而减小，说明j对i的贡献要小于离i更远的粒子对i的贡献，并且这种趋势随两点距离的减小而加剧，这便是压缩失稳产生的根本原因.因此，可将极值点左侧的区域称为压缩失稳区.

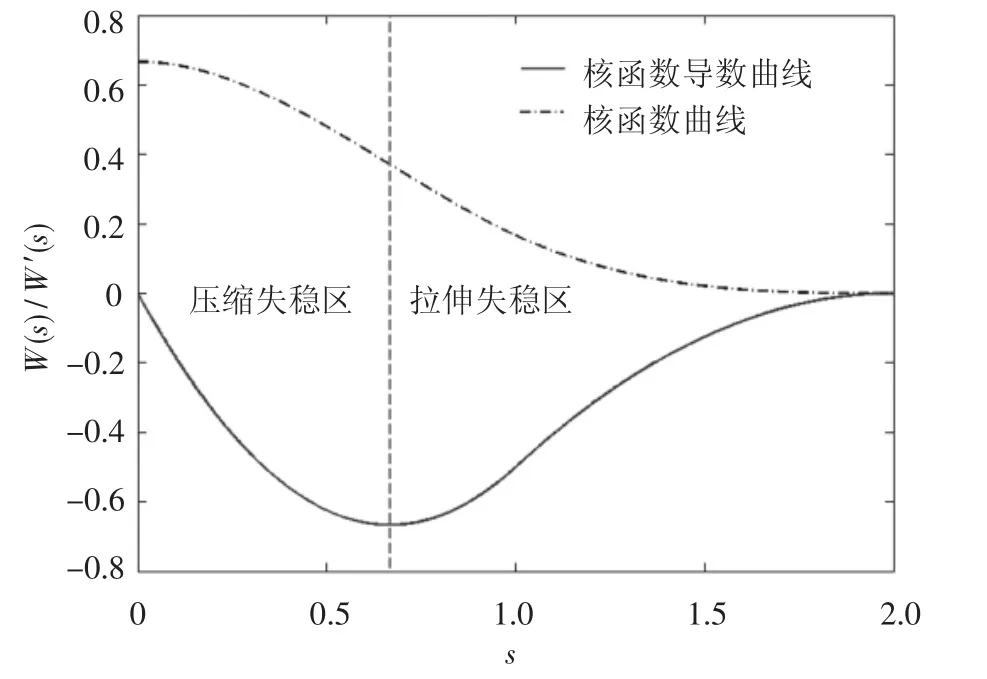
图1 三次B-Spline函数及其一阶导数曲线

2.2 消除压缩失稳的人工粘性

压缩失稳可通过引入人工粘性来解决.人工粘性的形式很多，但通常采用的形式包含两种不同类型的粘性，即适用于消除波后振荡的线性粘性Π =－αρlc▽·v和抑制冲击波强间断面数值振荡的二次粘性Π=βρl2(▽·v)2.其中:α和β是无量纲系数;l是激波长度传播尺度;c是声速.

将上述两种粘性考虑在一起，Monaghan J J等［14］给出了适合于SPH法的混合型人工粘性

引入人工粘性后，式(2)和式(3)分别变为

2.3 改进拉伸失稳的人工力

Swegle J W等［3］指出拉伸不稳定既不依赖于人工粘性，也不依赖于时间积分项，它是典型的与状态方程无关的问题，因为在状态方程中不产生拉伸应力.Monaghan J J等［10－11］提出了用于稳定计算的人工力，该力与具体的核函数有关，对于三阶B-Spline函数，当h＜rij≤2h时，

式中:rij为粒子i和粒子j的间距，h为两粒子平均光滑长度，σ和ρ分别为应力和密度;ε和n无量纲，通常为0.2和4.式(2)和式(3)分别变为

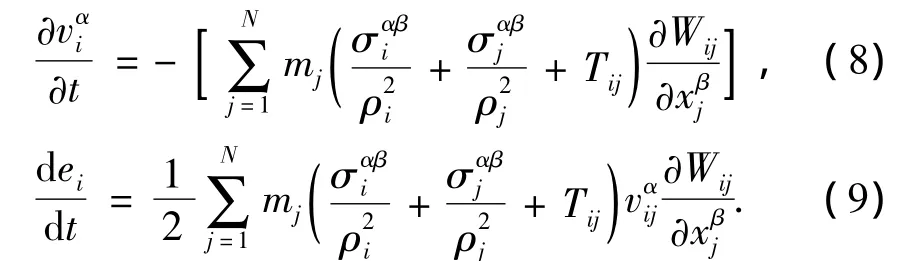
当rij=2h时式(8)和(9)不连续，而且当粒子间距rij增大时Tij大幅减小，难以抵消拉伸不稳定的影响.因此虽然在一定程度上解决了拉伸不稳定的问题，但依然存在一定的震荡.为了进一步解决拉伸不稳定问题，考虑到物体处于弹性拉伸时弹性模量乘以应变即是应力的现象，本文提出了如下形式的人工力:

式中，κ通常取0.1～0.3;E为弹性模量;α和β的取值范围通常为0.2～1.0和1.0～5.0.该人工力是连续的，其第一项随粒子间距rij增大而增大，与式(7)相比可更有效地抵消拉伸不稳定的影响;第二项为粒子分离时的人工粘性力［15］.该人工力起作用的条件为

1)粒子间距:当h＜rij≤2h时;

2)粒子反向运动:当vij·xij＞0时;

3)粒子状态:相互作用的粒子是固体，并且尚未失效;

4)粒子归属:相互作用的粒子属于同一物体.

对于二维和三维情况，Owen J M［16］提出了张量形式的人工粘性力，对消除压缩失稳得到了较好的结果.本文在该人工粘性力的基础上叠加抗拉伸不稳定的人工力，建立了统一形式的人工力，此时式(2)和式(3)分别变为

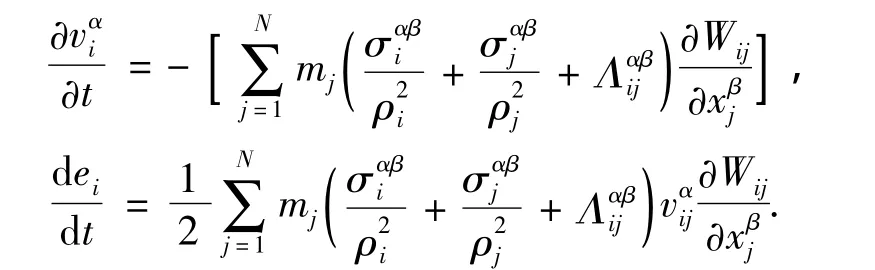
式中:统一张量形式的人工力Λαβij=Ταβij－Παβij，张量形式的人工粘性力Παβij有如下定义［16］:

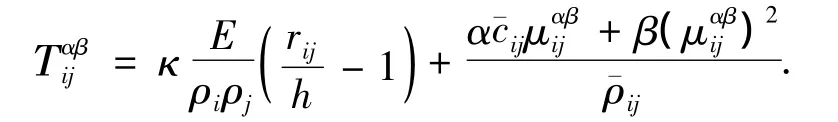
3 算例

3.1 算例1

设一维铝杆长 100 mm，左半部分具有－100 m/s的初速度，右半部分静止.由于拉力作用，应力波从中间向两侧传播.将该铝杆进行均匀离散，光滑长度取为0.1 mm，采用三阶B-Spline核函数和所提出的人工力，计算至5 μs.铝杆材料为 Al 2024，采用 Mie-Grüneisen状态方程和Johnson-Cook强度模型进行模拟，材料参数见表1和表2.

表1 Mie-Grüneisen状态方程参数

表2 Johnson-Cook强度模型参数

Mie-Grüneisen状态方程为

其中:pH=ρ0cμ(1+μ)/［1－(s－1)μ］2，eH= (pHμ)/(2ρ0(1+μ))，μ=(ρ/ρ0)－1，Γρ= Γ0ρ0=const，U=c0+sup.式中:p和e分别为静水压力和比内能;pH和eH分别为冲击Hugoniot曲线上静水压力和比内能的参考值;Γ和ρ分别为Grüneisun参数和密度，相应地 Γ0和 ρ0为初始Grüneisun参数和初始密度;U和up分别为冲击波波速和波后质点速度，c0为体积声速，s为U和up之间线性关系的斜率;μ为压缩比.

Johnson-Cook强度模型为

式中:σy为屈服应力;εp为等效塑性应变;˙εp为等效塑性应变率;参考应变率=1 s－1;若T为温度，TRoom为室温，TMelt为熔点，则T*=(T－TRoom)/ (TMelt－TRoom);A，B，n，C和m是材料常数.

图2 5 μs时杆中应力－位置曲线

计算得到的5 μs时杆中应力 －位置曲线如图2所示.其中，图(a)为通过Ansys Autodyn v6.1利用有限元法的计算结果，不会出现拉伸不稳定现象;图(b)中显示了没有施加人工力时SPH法产生了极度不稳定现象.当加入Monaghan J J等提出的人工力进行模拟后，结果如图(c)所示，其曲线整体趋势与图(a)相同，在一定程度上解决了拉伸不稳定的问题，但依然存在一定的振荡.使用本文的人工力后计算结果如图(d)所示，可以看出得到的曲线平滑且几乎不产生振荡，与有限元结果非常接近，拉伸不稳定性得到了较大改善，其效果优于Monaghan J J等提出的人工力.

3.2 算例2

设一维铝杆长 100 mm，左半部分具有－100 m/s的初速度，右半部分具有100 m/s的初速度.材料及离散方式与算例1相同，计算得到的5 μs时杆中应力－位置曲线如图3所示.

其中，通过Ansys Autodyn v6.1利用有限元法的计算结果如图(a)所示;图(b)显示了没有施加人工力时SPH法产生的极度不稳定现象.当加入Monaghan J J等提出的人工力进行模拟后，结果如图(c)所示.使用本文的人工力后计算结果如图(d)所示.从图中可以看出，通过施加本文人工力得到的曲线更加平滑且振荡较小，与有限元结果接近，其效果优于Monaghan J J等提出的人工力.

图3 5 μs时杆中应力－位置曲线

［1］LUCY L B.A numerical approach to the testing of the fission hypothesis［J］.Astronomical Journal，1977，82: 1013－1020.

［2］LIBERSKY L D，PETSCHEK A G，CARNEY T C，et al. High strain Lagrangian hydrodynamics:a three-dimensional SPH code for dynamic material response［J］.Journal of Computational Physics，1993，109(1):67－75.

［3］SWEGLE J W，HICKS D L，ATTAWAY S W.Smoothed Particle Hydrodynamics stability analysis［J］.Journal of Computational Physics，1995，116(1):123－134.

［4］MORRIS J P.Analysis of Smoothed Particle Hydrodynamics with applications［D］.Melbourne:Monash University，1996.

［5］WEN Y，HICKS D L，SWEGLE J W.Stabilizing SPH with conservative smoothing，SAND94－1932［R］.Albuquerque:Sandia National Laboratories，1994.

［6］BALSARA D S.Von Neumann stability analysis of Smoothed Particle Hydrodynamics－suggestions for optimal algorithms［J］.Journal of Computational Physics，1995，121(2):357－372.

［7］DYKA C T，INGEL R P.An approach for tension instability in Smoothed Particle Hydrodynamics［J］.Computers and Structures，1995，57(4):573－580.

［8］DYKA C T，RANDLES P W，INGEL R P.Stress points for tension instability in Smoothed Particle Hydrodynamics［J］.International Journal for Numerical Methods in Engineering，1997，40(13):2325－2341.

［9］RANDLES P W，LIBERSKY L D.Normalized SPH with stress points［J］.International Journal for Numerical Methods in Engineering，2000，47(10):1445－1462.

［10］MONAGHAN J J.SPH without a tensile instability［J］.Journal of Computational Physics，2000，159(2):290－311.

［11］GRAY J P，MONAGHAN J J，SWIFT R P.SPH elastic dynamics［J］.Computer Methods in Applied Mechanics and Engineering，2001，190(49－50):6641－6662.

［12］CUMMINS S J，RUDMAN M.An SPH projection method［J］.Journal of Computational Physics，1999，152 (2):584－607.

［13］MONAGHAN J J.Extrapolating B-Splines for interpolation［J］.Journal of Computational Physics，1985，60 (2):253－262.

［14］MONAGHAN J J，GINGOLD R A.Shock simulation by the particle method SPH［J］.Journal of Computational Physics，1983，52(2):374－389.

［15］SWEGLE J W，ATTAWAY S W，HEINSTEIN M W.An analysis ofSmoothed Particle Hydrodynamics，SAND93－2513［R］.Albuquerque:Sandia National Laboratories，1994.

［16］OWEN J M.A tensor artificial viscosity for SPH［J］.Journal of Computational Physics，2004，201(2):601－629.