结构损伤参量灵敏度分析的传感器数量位置优化

孙晓丹，欧进萍，2

(1.哈尔滨工业大学土木工程学院，哈尔滨150090，sunxiaodan0428@yeah.net; 2.大连理工大学土木水利工程学院，辽宁大连116024)

传感器优化布置包括传感器数目的优化和位置的优化，是结构健康监测中一个关键问题.关于传感器位置的优化提出了很多方法和准则，但对传感器数目优化的研究还非常少.传感器优化是一种多目标优化，以模态识别为目标的传感器优化比较多，但是损伤识别是结构状态评估的关键，以损伤识别为目标的传感器优化亟待解决.

近年来，以结构损伤识别为目标的传感器优化研究主要有:Cobb等［1］提出了一种对结构进行损伤监测的传感器布置方法.Shi等［2］通过仅考虑结构刚度变化的结构特征灵敏度分析，以结构各单元的损伤信息为条件，应用有效独立法进行了传感器优化布置.刘晖等［3］提出基于有限测点的结构损伤识别的柔度法，通过对结构柔度的灵敏度分析，以结构损伤信息为条件计算结构的Fisher信息阵，选择对结构柔度变化敏感的自由度为测点.

以上方法开启了以损伤识别为目标的传感器位置研究，但对其数目的研究非常少.本文以判断结构是否存在一定水平损伤为目标，以灵敏度技术为基础，以遗传算法为工具，针对各种损伤指标得出所需传感器的最小数目及其配置位置.

1 结构损伤参量的灵敏度分析

损伤参量对结构损伤的灵敏度是选取损伤参量的最主要依据.国内外研究者在应用灵敏度方法对结构进行损伤识别方面已经做了很多工作［4－5］，目前针对结构损伤识别的灵敏度计算方法主要有直接求导法、摄动法和伴随向量法.直接求导法由于其物理意义明晰、过程简明等特点而很早得到关注，Zhao等［4］通过直接求导灵敏度方法分析比较了频率、位移模态和柔度法的敏感性，在此研究基础上，本文对灵敏度推导方法进行改进:由于对刚度矩阵元素求导并没有直观的物理意义，所以本文将其改进为对各个单元刚度进行求导，这样得到的灵敏度将更直接地显示损伤随某个单元变化的趋势.以下将具体推导频率、位移模态、模态曲率、柔度矩阵、应变模态和模态应变能等损伤参量对单元刚度变化的灵敏度.

1.1 频率对单元刚度的灵敏度

一般说来，结构的损伤将引起结构刚度的降低而不引起质量的改变.因此，结构的特征灵敏度分析主要是模态参数对结构刚度的灵敏度分析.对于任意具有n个自由度的结构系统，其振动特征方程可归结为

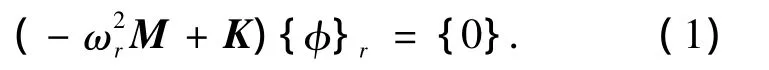
式中:r=1，2，…，n，M和K分别为结构质量和刚度矩阵;ωr为结构的第r阶固有圆频率，{φ}r为质量归一化的第r阶振型({φ}M{φ}r=1)，在本文的推导和计算中均以质量归一化的振型为标准.

将结构的振动特征方程对第i个单元刚度ki求导，可得

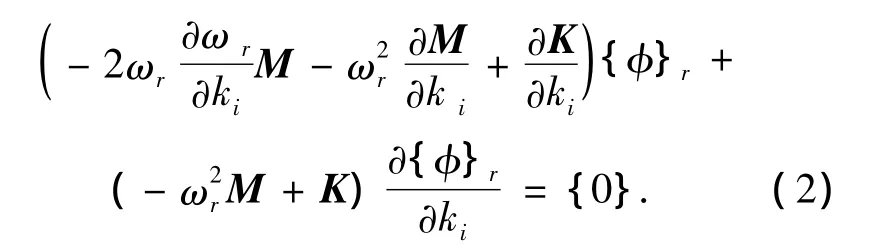
M与ki不相关，所以方程(2)两边同乘，由于振型的正交性成立，则可得频率对单元刚度ki的灵敏度:

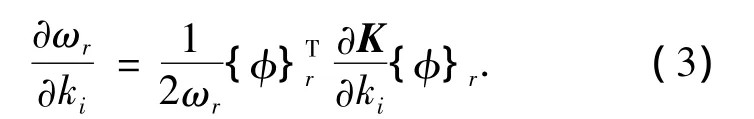
1.2 位移模态对单元刚度的灵敏度

由式(2)，得

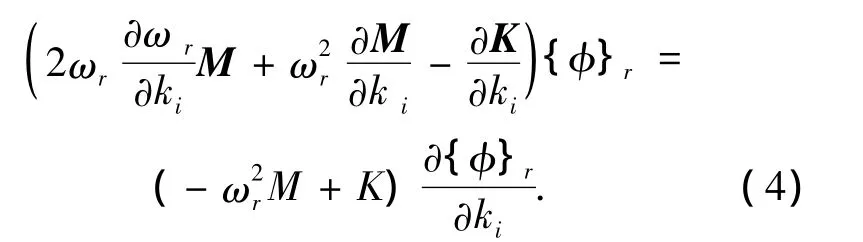
根据文献［6］，该式的解为

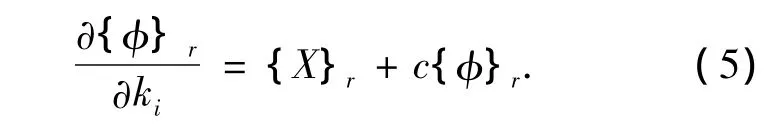
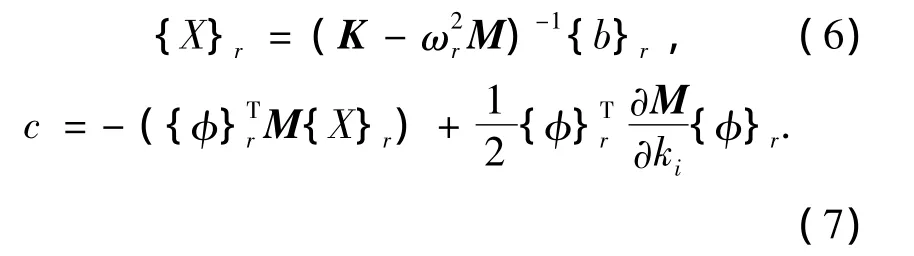
1.3 模态曲率对单元刚度的灵敏度

曲率是结构中性面的变形模态，与构件的截面弯曲刚度有关.如果构件发生损伤，损伤处的局部刚度会下降，则曲率会增大，因此根据振型曲率的变化可以定位损伤.曲率不能直接测量，一般通过测量位移模态利用中心差分方法求解得到结构的模态振型曲率，其计算表达式为

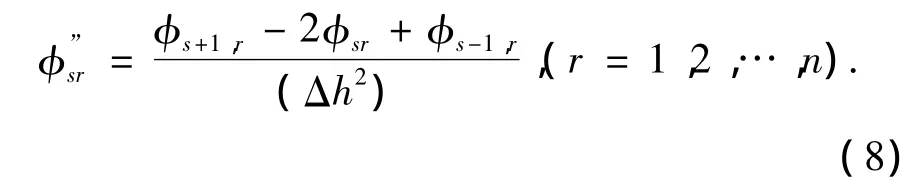
式中Δh=x(s+1)－x(s－1)为(s+1)测点和(s－1)测点的坐标之差.

对上式两端求对ki的一阶偏导数，可得位移模态曲率对ki的灵敏度:

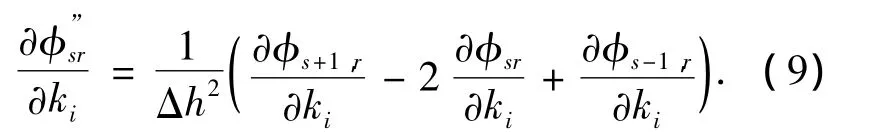
1.4 柔度矩阵对单元刚度的灵敏度

结构的柔度矩阵F可以近似地表示为

柔度矩阵中第r列、第s行元素可以表示为

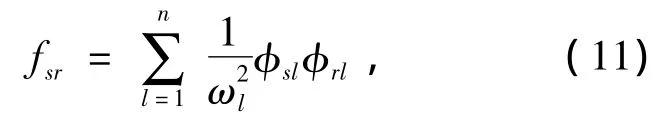
则柔度矩阵中第r列、第s行元素对第i单元刚度的灵敏度为

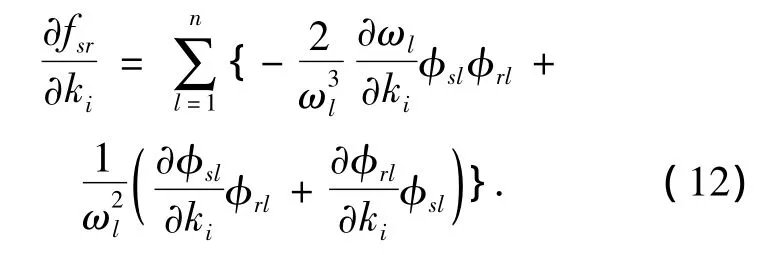
一般柔度法用柔度矩阵的对角线元素来识别损伤位置，所以当s=r时式(12)即为柔度参量对第i单元刚度变化的灵敏度.

1.5 应变模态对单元刚度的灵敏度

应变模态反应了结构的固有特征，也是表征结构是否损伤的参量之一.由材料力学关系，对于直梁截面可以得到

式中:ε为梁截面任一点的应变;z表示ε对应点处与梁中性层之间的距离.

由式(13)可以看出，应变模态与位移模态曲率只相差一个系数.利用中心差分方法求解得到结构的位移模态曲率，继而得到应变模态为

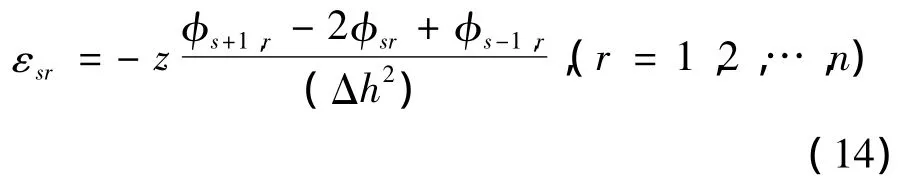
式(14)两端对i单元刚度求一阶偏导数，可得应变模态对单元刚度的灵敏度:

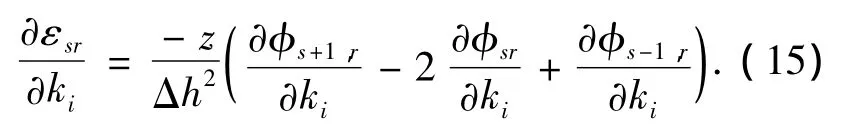
1.6 模态应变能对单元刚度的灵敏度

模态应变能是Kim和Stubbs在1993年提出的损伤参量，根据Stubbs，长度为l的欧拉梁的模态应变能U为

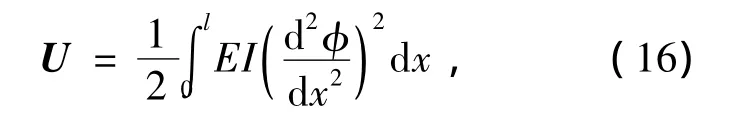
式中EI为梁段的截面弯曲刚度.对于均匀划分单元(长度为Δl)的有限元模型，梁区段模态应变能为

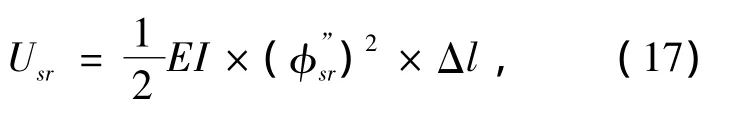
对方程(17)两端的单元刚度求偏导，可得模态应变能对单元刚度的灵敏度:

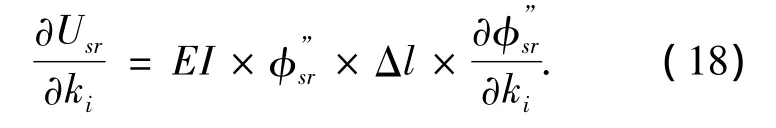
2 基于灵敏度分析的传感器数目与位置优化

结构损伤对各种损伤参量的影响范围是不同的，根据其影响范围可以进行测点数目的优化、并同时得到测点位置.基于损伤参量对结构损伤的灵敏度分析并应用遗传算法，以识别结构损伤位置为目标的传感器数目及其位置可按以下方法优化确定:

1)通过灵敏度分析和设定能识别出的损伤程度，确定损伤比较线:

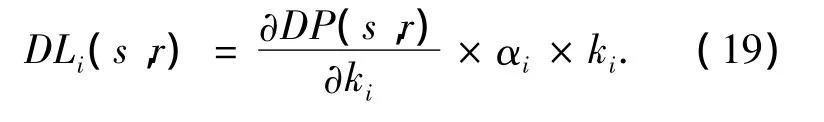
式中:DLi为第i单元的损伤比较线为损伤参量(damage parameters)对ki的灵敏度，αi为设定的第i单元的损伤程度.

2)通过噪声程度确定能识别的精度，当损伤小于该水平时，损伤引起的变化将淹没于噪声之中.

仿真分析中，噪声数据用输出加入一定水平的白噪声方式产生，即

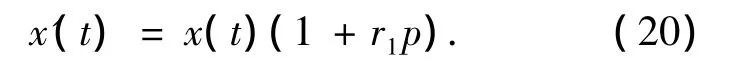
式中:x(t)为输出的加速度时程，r1为均值为0、方差为1的随机数;p代表噪声水平(%).通过N个x'(t)通过ERA和NExT联合算法［6］进行参数识别，可得相应的结构振型和频率，进而可以得到结构的损伤参量，对N个样本可以分别得到损伤参量(包括位移模态、柔度矩阵、模态曲率和模态应变能)的均值和方差σID.

因此，噪声比较线确定为

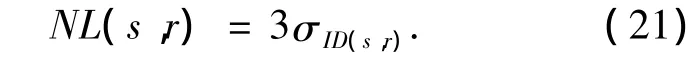
式中:NLi(s，r)为第i单元的噪声比较线，通过3σ准则确定临界值，临界值的数值为损伤参量方差的3倍.

3)通过遗传算法搜索最小的传感器数目及其配置方案.约束条件为

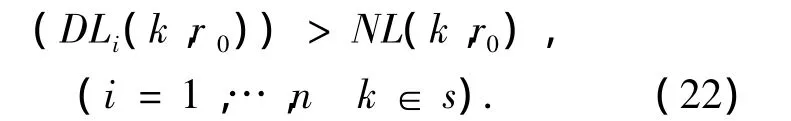
适应度函数为

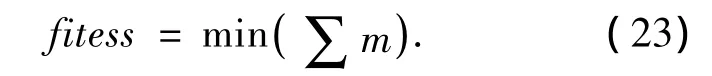
式中:k为传感器位置，m为传感器数目.式(22)含义为对于第ro阶模态、传感器位置k能够保证对于任意的i(i=1，…，n)单元的损伤比较线大于第ro阶模态、k位置的噪声线.

根据损伤参量对结构损伤的灵敏度特点(以下算例也将清楚看到)，可以把损伤参量分为两类，第一类参量的灵敏度不随测点变化而变化，如位移模态和柔度矩阵，这类问题可以通过遗传算法找到测出损伤所需最小的传感器数目及其布设位置;另一类参量的灵敏度随测点不同而变化，如模态曲率和模态应变能，这类参量是由位移模态经过中心差分法构造的，测点数目减少到一定程度时会使反应的损伤位置失真，所以另一个约束条件为

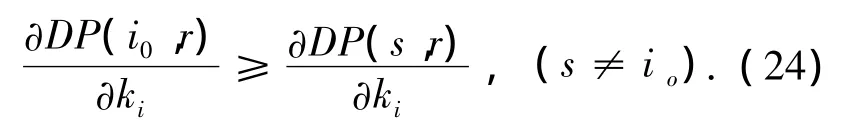
式中i0为所选测点位置中离i最近的位置.该约束条件保证了从结果可以看出损伤的位置.

3 仿真算例

本文采用20单元的简支梁有限元模型(见图1)进行数值模拟，分别得出每个损伤参量相对于单元刚度的灵敏度.该结构有60个自由度，本文仅关心竖向振型，因此对节点2到节点20竖向的19个自由度进行研究.其中，kn(n=1～20)为每个单元的竖向刚度.

3.1 结构损伤参量的灵敏度分析

本文采用目前结构分析比较成熟的商业通用软件ANSYS建立该结构的有限元模型，对模型进行基本的模态分析，所得灵敏度如图2所示.

图1 简支梁有限元模型及其截面

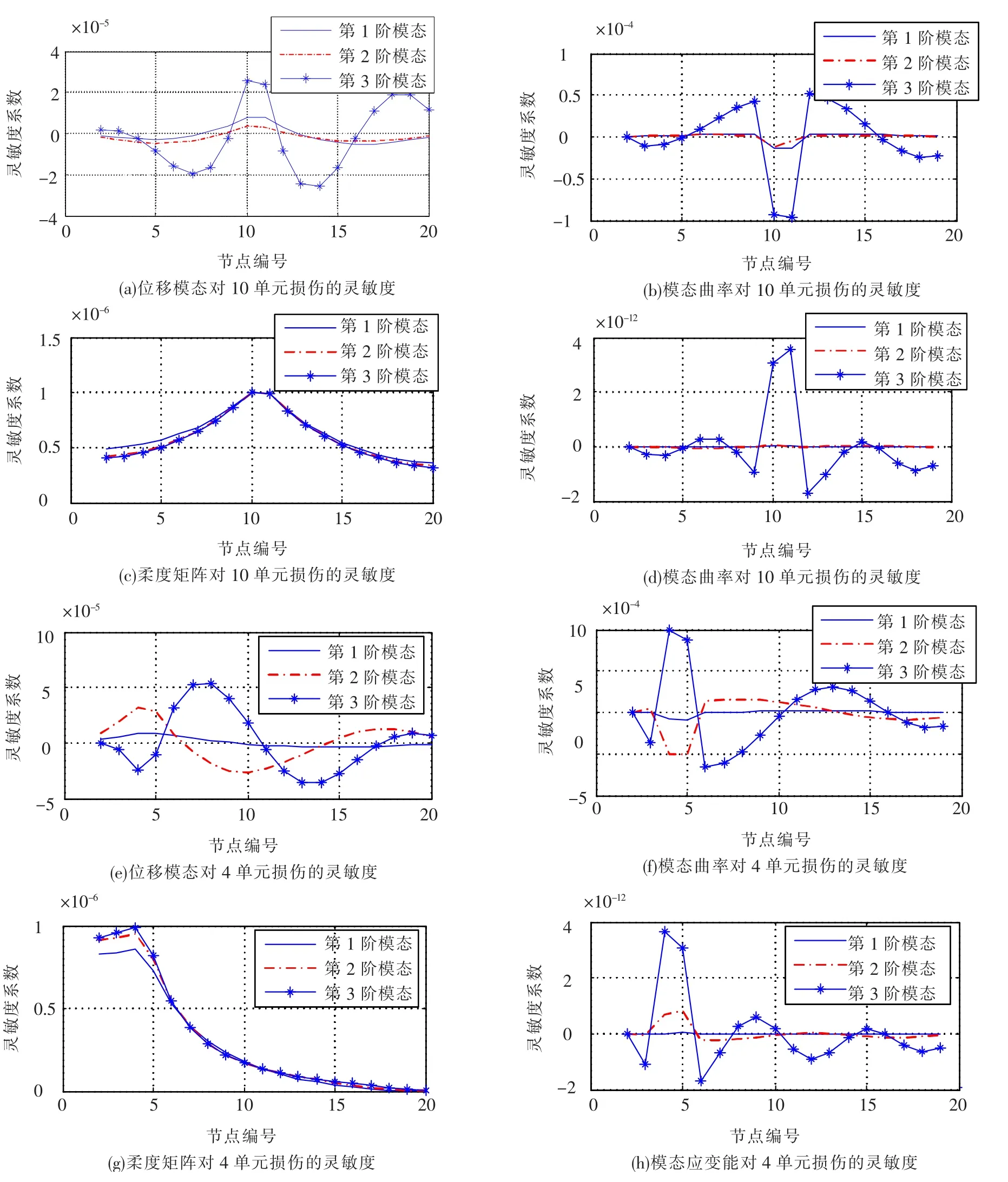
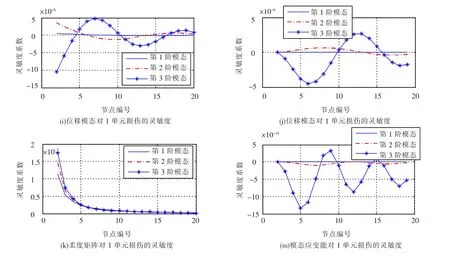
图2 损伤参量的灵敏度

观察位移模态、模态曲率、柔度矩阵和模态应变能等损伤参量前3阶模态灵敏度的特点，可以看出每种损伤参量的影响范围大不相同，位移模态与柔度矩阵整体性较强，而模态曲率和模态应变能局部性非常强.由于模态曲率和模态应变能采用差分法计算，边界处的损伤很难识别，这也是这两种方法的局限性.

根据对图2的观察，在单损伤的情况下，以上损伤参量均是靠近损伤位置的数值比较大.因此，在此情况下可确定损伤位置区间.位移模态的灵敏度特征具有很强的整体性，但是很难达到损伤局部定位的效果;柔度矩阵的灵敏度有如下特点:具有很强的整体性，但是损伤位置出现很明显的峰值，且两侧基本为单调函数，因此判别损伤位置比较容易;与位移模态和柔度矩阵不同，模态曲率和模态应变能的灵敏度随测点不同而变化.

3.2 传感器数目和位置优化

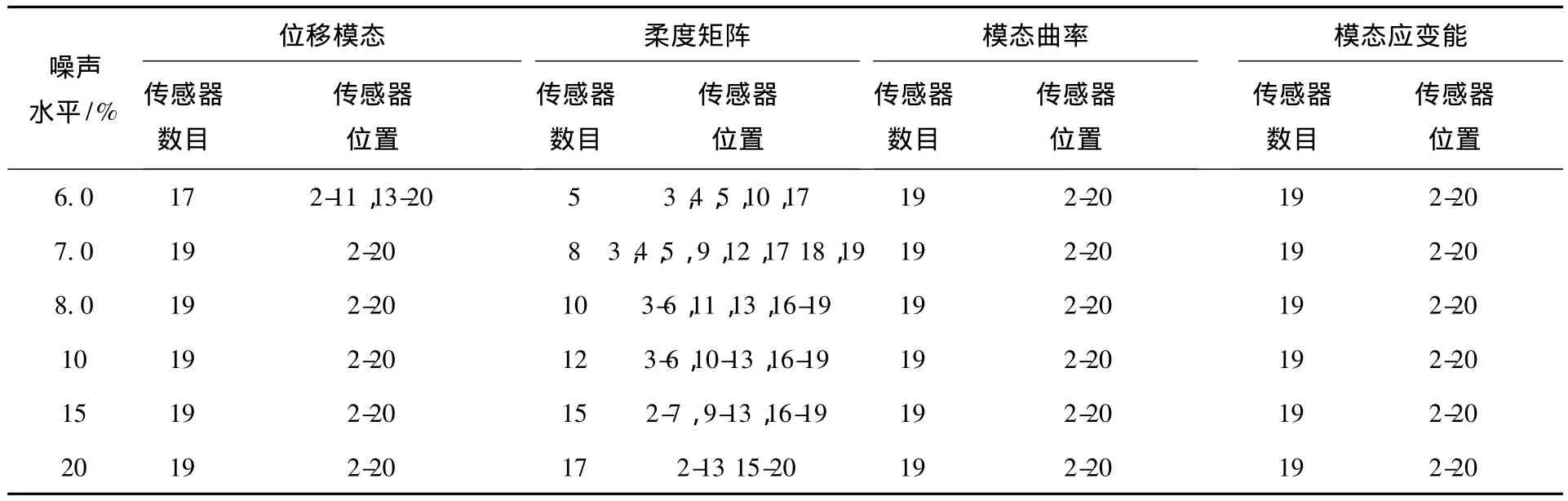
每个单元设定的可识别损伤程度均为αi= 10%，噪声水平分别设定0.5%，1%，1.5%，1.6%，1.8%，2%，3%，5%，6%，7%，8%，10%，15%，20%.应用以上方法计算得到相应于各种工况的传感器最小数目和位置如表1所示，各种损伤参量随噪声水平变化的传感器最小数目见图3.

根据表1和图3结果可知噪声水平越高所需传感器数目越多.损伤参量比较可知对于该算例位移模态和柔度矩阵所需传感器数目较少，而相应模态曲率和模态应变能配置的传感器数目较多.

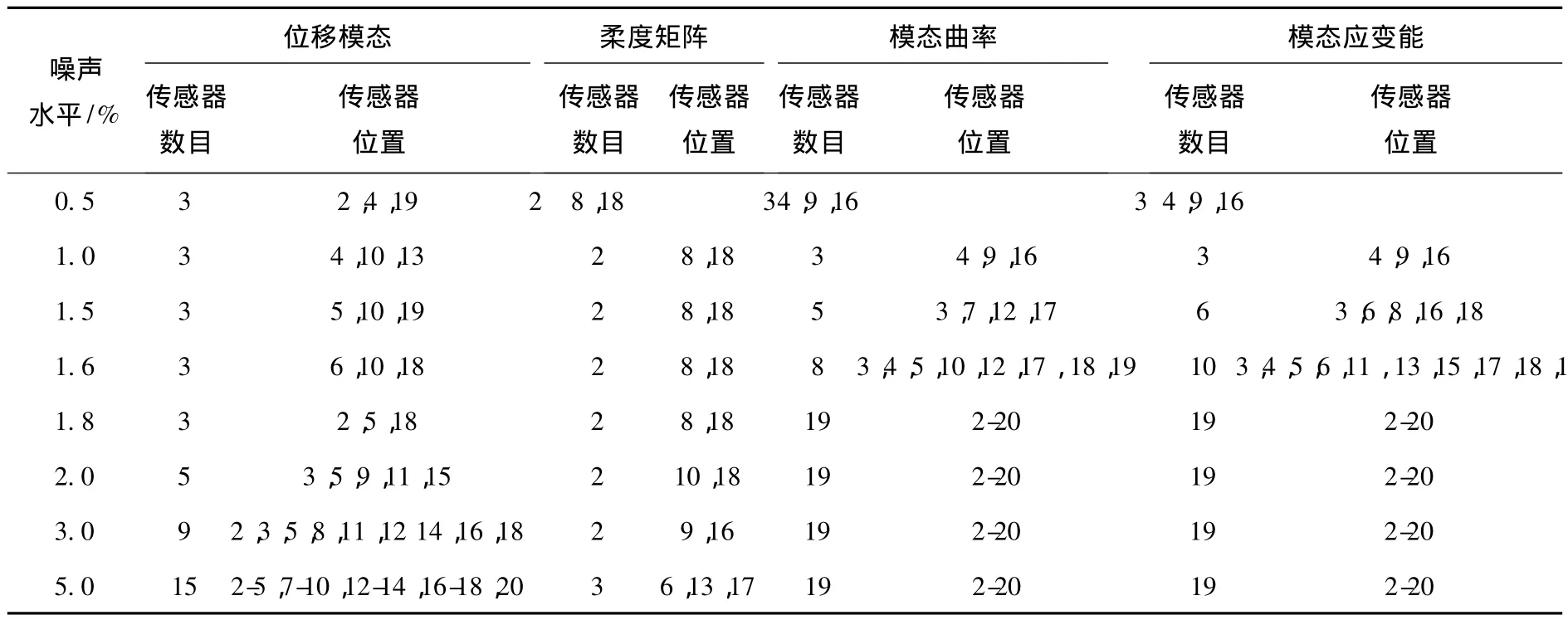
表1 传感器最小数目及其位置

续表1

4 结论

1)该传感器优化方法可以确定以识别一定程度的损伤为目标传感器的最小数目及其位置.并且对单损伤情况下结构的损伤位置有大致的判断，对多损伤情况时最大程度损伤的位置有预估.

2)提出的以上方法确定的传感器配置方案与结构单元的划分、每个单元待识别的损伤程度、选择的损伤参量以及环境噪声水平有关.需要识别的程度越小就需要更多的传感器.噪声水平越高，所需传感器越多.此外，选择的模态阶数对优化结果也有重要影响.

3)采用不同的损伤参量进行损伤识别，就会有不同的传感器布置方案，在本文研究的几种损伤指标中，对于该算例，柔度法所需传感器数目较少，但是损伤位置比较难确定，而对于模态曲率和模态应变能所需传感器比较多.

［1］ COBB G，LIEBST B S.Sensor placement and structural damage identification from minimal sensor information［J］.AIAA Journal，1997，35(2):369－374.

［2］ SHI Z Y，LAW S S，Zhang L M.Optimum sensor placement for structural damage detection［J］.Journal of Engineering Mechanics，2000，126(11):1173－1179.

［3］ 刘晖，瞿伟廉，袁润章.基于有限测点信息的结构损伤识别柔度法［J］.计算力学学报，2005，22 (3):379－384.

［4］ ZHAO Jun，DEWOLF J T.Sensitivity study for vibrational parameters used in damage detection［J］.Journal of Structure Engineering，ASCE，1999，125(4): 410－416.

［5］ NELSON R B.Simplified calculation of eigenvector derivatives［J］.AIAA Journal，1976，14(9):1201－1205.

［6］ 侯立群.环境激励与噪声干扰下斜拉桥模态识别与损伤定位［D］.哈尔滨:哈尔滨工业大学，2004.