1-3型压电复合材料发射换能器研究

张 凯,蓝 宇,李 琪,顾郑强

(哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 150001)

1-3型压电复合材料发射换能器具有很多优点:重量轻、易于共形、声阻抗低、带宽较宽、换能器的有效机电耦合系数高,接近于压电陶瓷相的k33. 20世纪70年代末,美国宾州州立大学的Newnham教授首先提出了 1-3型压电复合材料的概念[1],在此基础上人们对其进行了广泛的研究[2].在解析理论方面,主要有美国海军实验室W.A.Smith提出的厚度模式理论[3]和澳大利亚Helen laiWah Chan提出的均匀理论模型[4].在数值计算方面,英国斯特莱斯克莱德大学的G.Hayward等人利用有限元软件ANSYS分析了1-3型压电复合材料换能器的工作特性[5-7];法国的Anne-Christine等人利用有限元软件ATILA分析了1-3型压电复合材料换能器的工作性能[8].之前的有限元分析都假设 1-3型压电复合材料为无限大平板,通过分析它的一个周期特性来近似得到1-3压电复合材料的特性,而印度的 R. Ramesh等人建立了完整的1-3型压电复合材料有限元模型并对其进行了分析[9].

1-3型压电复合材料完整模型的节点数非常多,因而会花费很长的计算时间;而周期模型又不能直接模拟 1-3型压电复合材料换能器在水中的响应特性.本文利用功率守恒的原理得到了周期模型分析 1-3型压电复合材料发射器特性的有限元分析方法;同时利用厚度模式理论和所得的有限元方法设计了 1-3型压电复合材料发射换能器,制作并测试了一个高频复合材料发射换能器.

1 1-3型压电复合材料的概念

1-3型压电复合材料是由一维连通的压电相小柱平行排列于三维连通的聚合物相基体中而构成的两相压电复合材料,其极化方向与压电相小柱高度方向相同.常用的压电相材料有PZT4、PZT5和弛豫铁电单晶等;常用的聚合物相材料有环氧树脂、聚氨酯和聚亚胺酯等.1-3型压电复合材料的示意图如图1所示.

图 1 1-3型压电复合材料结构示意图Fig.1 Schematic representation of 1-3 piezocompositematerial

2 厚度模式理论分析

1-3型压电复合材料的厚度模式理论[3]主要应用于水声发射换能器以及医疗超声换能器.在此应用中,换能器的工作频率接近于复合材料的厚度共振频率,复合材料中产生的应变波半波长接近于复合材料的厚度.1-3型压电复合材料等效参数的表达式是由陶瓷相体积百分数和陶瓷相、聚合物相的物理性能参数表达的.由复合材料等效性能参数和等效电路理论可以算出 1-3型压电复合材料的厚度机电耦合系数、特性阻抗以及纵波波速.

厚度机电耦合系数:

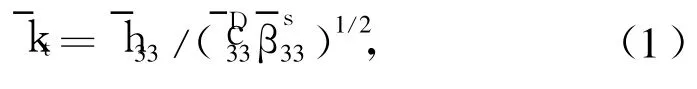
特性阻抗:

纵波波速:

由式(3)可得出1-3型压电复合材料的厚度共振频率:

式中:h为压电劲度常数,c为弹性常数,β为介电隔离率,ρ为密度,t为 1-3型压电复合材料的厚度,上面有横杠的参数为 1-3型压电复合材料的等效材料常数.

图 2 等效参数随压电相体积百分数的变化图Fig.2 The variation of equivalent parameters with volume fraction of piezoelectric phase

取压电相材料为PZT4,聚合物相材料为环氧树脂,如图2.

由图2(a)可知:当陶瓷相体积百分数为30%～80%时,1-3型压电复合材料的厚度机电耦合系数达到了最大值且基本恒定,这是因为在体积百分数较小时,大量的聚合物环绕着坚硬的压电陶瓷小柱,相当于压电陶瓷小柱受到了弹性边界载荷,使厚度机电耦合系数变小;当体积百分数较大时,由于聚合物对压电小柱的侧向夹持作用加大,致使厚度机电耦合系数减小;体积百分数适中时,弹性边界约束和夹持边界约束都比较小,致使厚度机电耦合系数变大.

由图2(b)可知:特性阻抗基本上随陶瓷相体积百分数增加而线性增长,这是因为陶瓷相的特性阻抗远远大于聚合物相的特性阻抗.

总之，小说教学中进行自主性阅读教育重在培养学生的探究能力和创新能力。作为教师，要善于给学生创造参与的机会和展示自我的机会，使学生在自主体验、自主感悟、自主质疑问难、自主发表见解的过程中，把书本知识变成自己的精神财富和阅读理解能力。

由图2(c)可知:纵波波速随压电陶瓷相体积百分数的增加而增加,那么厚度共振频率也随着体积百分数的增加而增加,这是因为陶瓷相的刚度比聚合物相的大很多,当陶瓷相体积百分数增加时,1-3型压电复合材料的刚度也在增加,频率也随之升高.

3 有限元分析

3.1 有限元分析的理论基础

利用ANSYS建立的整个1-3型压电复合材料发射器有限元模型的运算时间会很长,由于 1-3型压电复合材料具有二维周期性的特点,因此可以通过分析 1-3型压电复合材料中的一个周期的性能来分析1-3型压电复合材料发射器的性能.

在 1-3型压电复合材料发射器中,除了边缘处的周期单元,其他单元的负载基本相同,此时只需分析其中的一个周期单元.这样可以认为单个周期单元处于一刚性壁波导中的一端,而在波导的另一端施加边界条件.然后,可以利用ANSYS软件计算出波导水柱中的声压.

最后可以利用波导中的声压得出 1-3型压电复合材料发射器的远场声压.而波导中的波可视为声压为pp和质点振速为pp/ρc的平面波.假设所有周期法向振速相同,ρc负载相同,那么由功率守恒原理可得,1-3型压电复合材料发射器的总辐射功率为所有周期辐射功率之和:

式中:N为周期数,A为单个周期面积.由指向性因数的概念可知,上述功率与远场声强的关系为

其中,p为距离 1-3型压电复合材料发射器声轴方向r处的远场声压.

由于平面活塞辐射器的指向性因数[10]为

从而可得pp(ANSYS计算的值)与p的关系为

由于 1-3型压电复合材料发射器的边缘周期声负载比中间周期的小,式(8)只是一个近似解.因此解的精确性依赖于边缘周期的数量.

3.2 有限元模型的建立

在分析时只建立一个周期(一个周期包含一根压电陶瓷小柱及其周围的环氧树脂)的有限元模型,在边界上施加一定边界条件来模拟整个 1-3型压电复合材料发射器.利用ANSYS软件来建模,压电相为PZT4,聚合物相为环氧树脂,复合材料的压电相体积百分数为 60%,复合材料圆片的厚度为5mm,周期数为1 696个.为节省计算时间,只建立了一个周期的 1/4有限元模型,流体域为一刚性壁波导,如图3所示.

图 3 1-3型压电复合材料发射器一个周期的 1/4有限元模型Fig.3 The one-fourth finite elementmodel for a unite cell of the 1-3 piezocomposite projector

3.3 模态分析

通过对 1-3型压电复合材料一个周期的有限元模型进行模态分析,可得到复合材料的厚度共振频率和模态振型.

由以上分析可知 1-3型压电复合材料的厚度共振频率为318 kHz,振型如图4所示.

图4 1-3型压电复合材料发射器的厚度共振模态Fig.4 The thicknessmode of a 1-3 piezocomposite projector

3.4 谐响应分析

利用ANSYS软件提供的谐波响应分析功能,计算出换能器在流体中的导纳曲线,如图5所示.

图 5 1-3型压电复合材料发射器在水中的导纳曲线Fig.5 The admittance of a 1-3 piezocomposite projector in water

从图5可知:1-3型压电复合材料发射器在水中的谐振频率为323 kHz,电导峰值为18mS.1-3型压电复合材料发射器在水中的谐振频率比空气中的高5 kHz.

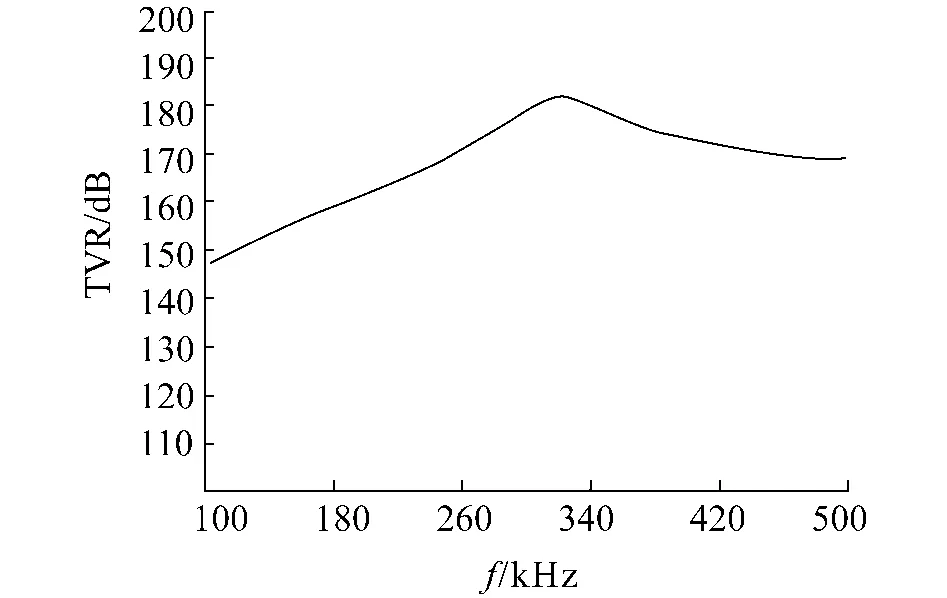
图6 1-3型压电复合材料发射器的发射电压响应Fig.6 The transmitting voltage response ofa 1-3 piezocomposite projector

利用ANSYS软件提供的流固耦合分析功能,计算出刚性壁波导中的声压,再由式(8)得出整个1-3型压电复合材料发射换能器的远场声压,从而可知流体中换能器的发射电压响应,如图6所示.

从图6可知:1-3型压电复合材料发射器在水中的谐振频率为 323 kHz,发射电压响应峰值为181 dB.

4 试验分析

按照设计尺寸制作了 1-3型压电复合材料发射换能器,如图7所示.

图 7 1-3型压电复合材料发射换能器示意图Fig.7 Schematic representation ofa 1-3 piezocomposite projector

利用HP4194阻抗分析仪测量了换能器在空气中和水中的频率特性和阻抗特性,如图8所示.

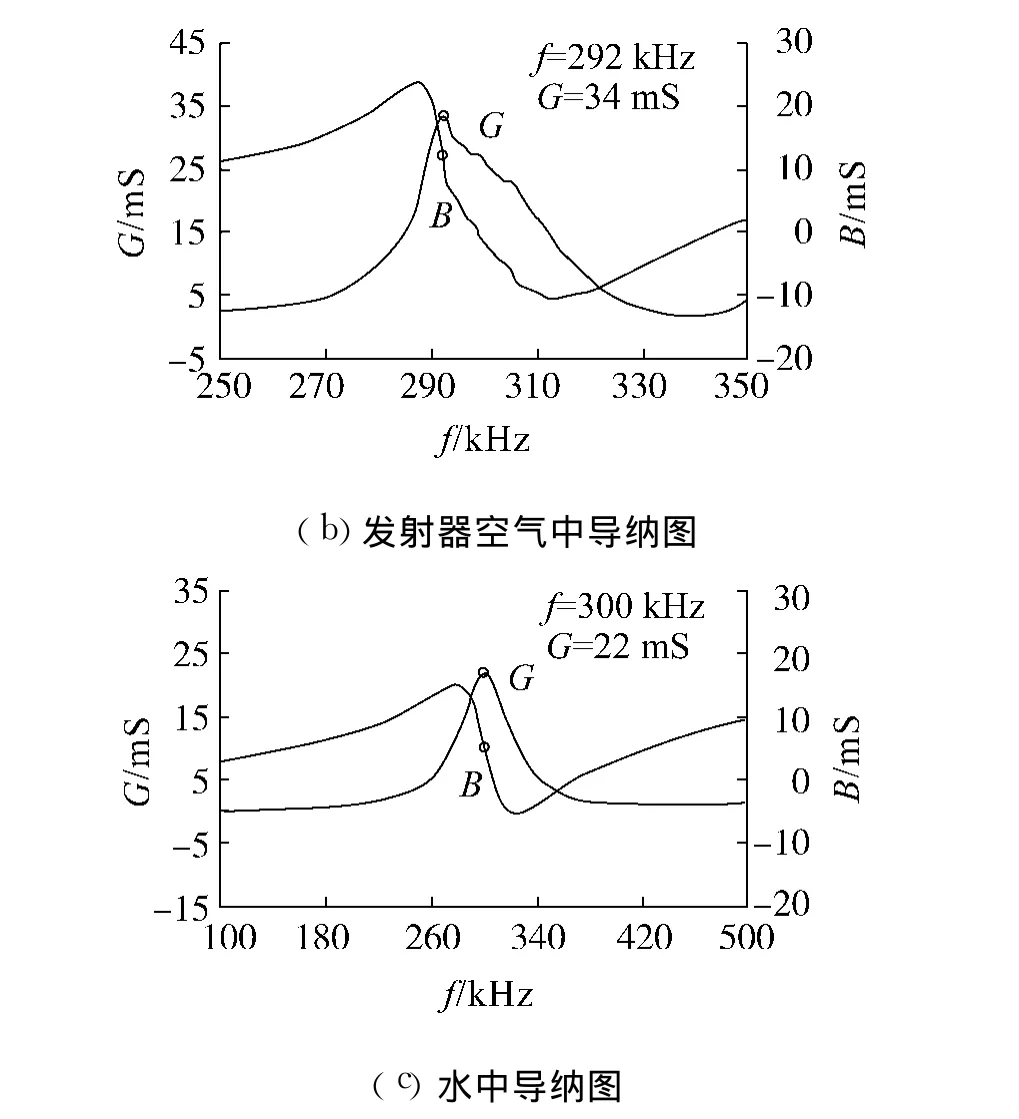
图 8 1-3型压电复合材料发射换能器的测试导纳图Fig.8 Themeasured admittance of a 1-3 piezocomposite p rojector

由图8可知:当灌注聚氨酯胶层时谐振频率由308 kHz降到292 kHz,这是因为用于防水的聚氨酯层相当于在换能器表面上增加了质量负载,从而降低了换能器的谐振频率.而 1-3型压电复合材料发射器在水中的谐振频率为 300 kHz,比空气中的谐振频率增加了 8 kHz,这与有限元法得到变化趋势相同.

将空气中的计算结果与实测结果的对比列于表1所示.对比结果可以看出,厚度模式理论和ANSYS的计算误差都很小,与实际测量结果符合良好,说明厚度模式理论和ANSYS软件可以应用于1-3型压电复合材料发射换能器的设计当中.

表1 1-3型压电复合材料空气中的理论计算结果与实际测试结果的比较Tab le 1 The comparison between the theoretical results and measured results of the 1-3 piezocompositematerial in air

在水池利用脉冲法测量了发射器的发射电压响应,其结果如图9所示.由图可知测得的1-3型压电复合材料发射换能器在水中的谐振频率为300 kHz,发射电压响应峰值为178 dB.

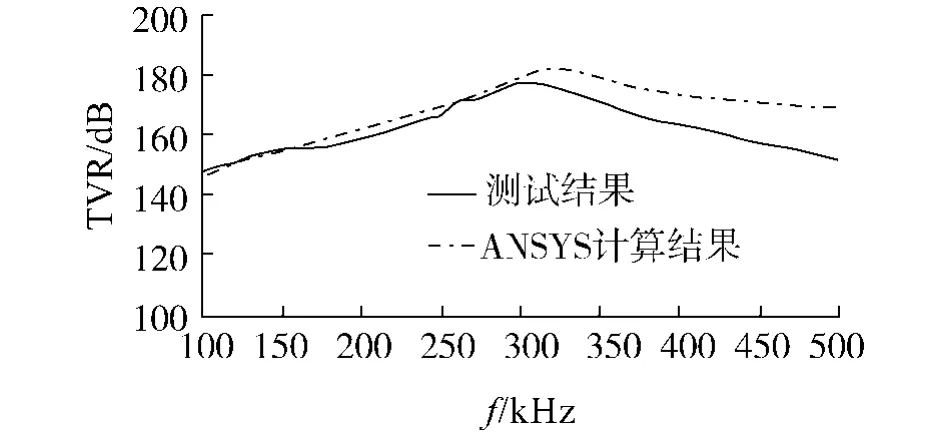
图 9 1-3型压电复合材料发射器的测试发射电压响应Fig.9 Themeasured transmitting voltage response of a 1-3 piezocomposite projector

从测试结果与计算结果的对比可以看出,无论是导纳曲线还是发射电压响应曲线,计算与测试的趋势基本一致,但还存在一定的误差:

1)实测共振频率比计算共振频率小.这是因为在有限元分析时,并没有考虑到用于防水的聚氨酯层,它相当于在换能器表面上增加了负载,从而降低了换能器的共振频率;并且利用切割浇注法制作的1-3型压电复合材料的结构尺寸存在误差,图 8(a)所示的导纳曲线形状畸变也说明了复合材料的结构尺寸存在误差.

2)当频率大于谐振频率时,实测发射电压响应比ANSYS计算结果偏小.这是因为灌注聚氨酯在高频时的损耗增加,而且在ANSYS计算时取的阻尼值为常数,而实际中阻尼应随频率的增加而增加.

5 结束语

本文设计了一个在水中谐振频率为 323 kHz,发射电压响应峰值为 181dB的1-3型压电复合材料换能器.并且按照设计尺寸制作并测试该压电复合材料发射器,其水中谐振频率为300 kHz,发射电压响应峰值为178 dB.结果表明:所用有限元法的仿真结果与实际测试结果吻合较好,本文提出的1-3型压电复合材料发射器有限元设计方法具有实用性.

[1]NEWNHAM R E,SKINNER D P,CROSS L E.Connectivity and piezoelectric-pyroelectric composites[J].Mat Res Bull,1978,13(5):525-536.

[2]TRESSLER J F,ALKOY S,DOGAN A,et al.Functional composites for sensors,actuators,and transducers[J]. Composite,1999,Part A 30:477-482.

[3]SMITH W A,AULD B A.Modeling 1-3 composite piezoelectrics:thickness-mode oscillations[J].IEEE Trans Ultrason Ferroelec Freq Contr,1991,38(1):40-47.

[4]CHANW LH,UNSWORTH J.Simp lemodel for piezoelectric ceram ic/polymer 1-3 composites used in ultrasonic transducer applications[J].IEEE Trans Ultrason Ferroelec Freq Contr,1989,36(4):434-441.

[5]JOHN A H,GORDON H.Finite-element analysis of 1-3 composite transducers[J].IEEE Trans Ultrason Ferroelec Freq Contr,1991,38(6):618-629.

[6]JEREMY B,GORDON H.Design of piezocomposite hydrostatic transducers using finite element analysis[C]//IEEE Ultrasonics Symposium,Cannes,France,1994.

[7]GORDON H,JEREMY B.Assessing the influence of pillar aspect ratio on the behavior of 1-3 connectivity composite transducers[J].IEEE Trans Ultrason Ferroelec Freq Contr, 1996,43(1):98-108.

[8]CHRISTINE A,HENNION H,DECARPIGNY J N.Finite elementmodeling of active periodic structures:application to 1-3 piezocomposites[J].J Acoust Soc Am,1993,94(2): 621-635.

[9]RAMESH R,PRASADC D,VINOD KUMAR T K.Experimental and finite element modeling studies on single-layer andmulti-layer 1-3 piezocomposite transducers[J].Ultrasonics,2006,44(2006):341-349.

[10]CHARLES H S,GOHN L B.Transducers and arrays for underwater sound[M].German:Springer,2006:451.