基于卡方分布的更新函数确定
田永涛,彭丽莉,周传斌
(重庆师范大学数计学院,重庆400047)
1 χ2更新过程
定义1[1]设ζ1,ζ2,ζ3,…是独立同服从自由度为k(k为偶数)的χ2分布,

并记
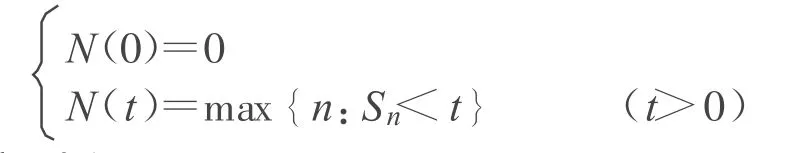
则称{N(t),t≥0}为χ2更新过程。
2 预备定理
引理1[2-3]Sn服从自由度为nk的χ2分布,其密度函数为
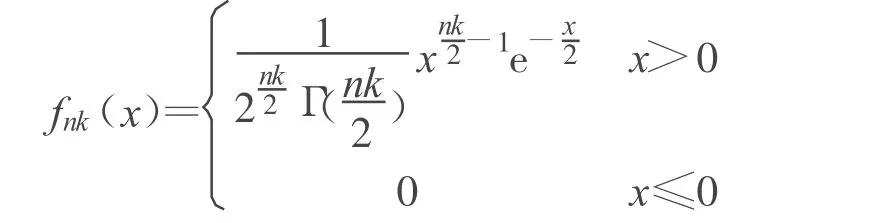
引理2[4]设{ζi}(i=1,2,…)是独立同服从自由度为k(k为偶数)的χ2分布,{N(t),t≥0}是以为更新间距的更新过程,则



3 卡方更新过程的更新函数
定理 卡方更新过程的更新函数


4 应用
实例[5]在公路桥梁上某一位置观测车辆到达的时间间隔20个数据(秒),从小到大排列为:3,4,4,6,6,6,8,8,10,11,13,21,29,42,45,48,49,55,59,68。用矩法估计χ2分布的参数k=[24.75]=24。经k-s检验结果观察值Dn=6.627 3×10-6。
对α=0.05,查k-s表临界值D20.005=0.294,有Dn=6.627 3×10-6<0.294=D20.005,所以,车辆到达时间间隔可以用χ2分布来描述。
我们可以将车辆到达时间间隔ζi视为服从自由度k=24的χ2分布,由于车辆到达时间间隔为独立同分布的,所以N(t)-[0,t)内经过的车辆数为χ2更新过程,由以上得出的χ2更新过程的更新函数即可得出在[0,t)内经过桥梁的平均车辆数。
[1] 林升光.结构应力S(t)为χ2-更新过程时最大值概率分布及统计参数的估计[J].数理统计与应用概率,1994,12(4):45-51.
[2] 胡迪鹤.应用随机过程引论[M].哈尔滨:哈尔滨工业大学出版社,1984.
[3] 孙荣恒.随机过程及其应用[M].北京:清华大学出版社,2004.
[4] 徐安.基于威布尔分布的更新函数确定方法研究[J].山东交通学院学报,2006,9:16-19.
[5] 林升光.应力S(t)为复合χ2-更新过程时结构可靠度渐近正态估计[J].数学物理学报,2001,21A(2):245-251.

