基于标准棋盘格的图像校准方法
李久芳
(中国电子科技集团公司第四十五研究所,北京 101601)
CCD摄像机在用镜头光学器件取景进行图像采集时,由于受对象与摄像机三维空间位置关系、镜头畸变和摄像机质量等因素的影响,成像系统与理想针孔模型不一致,采集到的图像存在几何畸变,特别是在使用广角镜头的时候,径向畸变会严重影响图像质量,给图像处理带来困难。因此,在进行基于图像分析的模式匹配、运动检测等定量分析时,就需要对有几何畸变的图像进行校正或对摄像机进行几何标定。
采用数字图像处理方法将畸变图像变换成原始图像,变换过程分为两步:(1)几何变换。即利用原图像与畸变图像的坐标关系,也就是畸变规律对畸变图像所在的坐标空间进行几何变换。根据几何变换找出图像畸变的每个区域的变形量,并建立查找表;(2)灰度校正。对采集的畸变图像查找并分析特征点,计算出变形量,然后修正,得到校准后的图像。本文主要实现用仿射模型和标准的棋盘格模型对机器视觉造成的畸变图像进行几何校正。
1 仿射变换
仿射模型采用的是与畸变相反的仿射变换来抵消图像的畸变,先恢复图像的变形角度,再对图像进行距离变换。这里以图像的中心为坐标原点。提取畸变图像上特征点,再利用仿射变换对图像进行旋转、平移,实现对图像的校正。
仿射模型作为多项式模型的一种特例,当图像获取系统各个光轴基本平行且目标距离较远时,忽略伴随的几何畸变,可以认为图像间只有二维平行、旋转和比例变化,图像间的变换关系可以由一个仿射模型来描述。
仿射变换的定义:若变换S∶Rn→Rn,S(x)=T(x)+a,T是非奇异线性变换,a∈Rn,则变换S称为仿射变换。二维图像仿射变换可以表示为:

其中,A是变形矩阵,B是平移矢量。二维空间中,仿射变换的变形矩阵可按如下4个步骤来分解:尺度、伸缩、扭曲、旋转。

可以看出,仿射变换包含了图像的几种典型低阶畸变。由于图像的畸变是一个连续的过程,几何畸变的变化量是有限度的,因此可假设仿射变换作为局部形变的模型。
可以将仿射模型简化为:

(x',y')为采集到图像的坐标位置,(x,y)为对应的点在未产生畸变的图像的坐标值。

图1 未产生畸变的图像

图2 采集的畸变图像
2 特征点的提取
特征点可分为两类:狭义特征点和广义特征点。狭义特征点是针对点本身定义的,其位置具有常规的属性意义,如边缘点、角点、交叉点等。广义特征点是基于区域来定义的,只代表满足一定特征条件的特征区域的位置。广义特征点可以使某个特征区域的中心、重心或特征区域的任何一个相对位置。本文所指的特征点是指广义特征点。
本文对特征点的提取是指提取标准棋盘格中的每个黑色和白色区域的重心。重心就是求物体(或区域)中像素坐标的平均值,(见公式8)。其中(xi,y1)为区域内像素的坐标,(x0,y0)为其重心坐标。
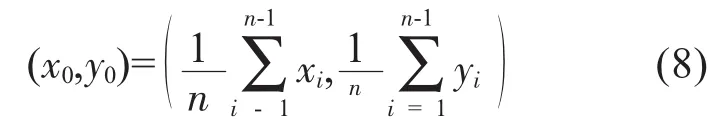
假如图像没有产生畸变,如图1所示,在这里需要根据CCD的分辨率和镜头的倍率算出实际成像系统的分辨率(见公式9),根据成像系统的分辨率,将标准棋盘格上的特征点转化为像素的相对坐标值。这就需要知道标准棋盘格的物理尺寸及其他相关参数。

x向相对坐标值=x向相对位置×成像系统的x向分辨率
y向相对坐标值=y向相对位置×成像系统的y向分辨率
因此只要知道标准棋盘格上的每个区域的中心间距,便可根据上面的公式计算出像素的相对坐标值。
对于采集到的畸变图像,如图2所示,对图像进行图像增强、平滑滤波、二值化得到二值图像,然后对得到的二值图像进行图像形态处理(先“膨胀”后“腐蚀”),之后再将这些二值化的图像连接成几何相关的区域,将标记后的区域,按照尺寸大小进行排序,通过设置阈值,去除小的区域。
在得到7×9的分块区域后,对区域分块标记进行深入的研究,能够快速地对每个特征点进行特征提取。图3为图像处理流程。

图3 特征点的提取
3 图像与运算



4 实验结果与分析


图4 采集的畸变图像

图5 校正后的图像
[1]徐慧.Visual C++数字图像实用工程案例精选[M].北京:人民邮电出版社,2004.
[2]陈兵旗,孙明.Visual C++实用图像处理专业教程[M].北京:清华大学出版社,2004.

