武广高铁沿线红黏土自振柱试验研究

刘晓红,杨果林,方 薇

(1.中南大学土木建筑学院,湖南长沙 410075; 2.湖南理工学院土木建筑系,湖南岳阳 414000)

武广客运专线是我国第一条全程无碴轨道时速达350 km的高速铁路,也是我国目前里程最长、技术标准最高、投资最大的客运专线。武广高速铁路的高标准技术主要表现在高平顺性、高动力稳定性、高精度、小残变、少维修等方面。基床是路基直接承受列车荷载的部分,基床的动力稳定是无碴轨道板寿命的保证。在列车重复荷载作用下路基所产生的累积永久下沉(残余变形)会造成轨道的不平顺,因此要求路基具有足够的强度、刚度和动力稳定性。土的动力参数是评价路基动力稳定的必要前提。动剪模量和阻尼比是描述土动力特性的两个重要参数,对场地土的共振、滤波和放大效应等具有显著的影响[1]。目前,国内外对多类土的动力特性进行了广泛的研究[2-5],但还未见有关原状结构红黏土动力特性研究的文献报导。根据工程勘察报告,武广高速铁路武汉至韶关段分布近 100 km的石灰岩类红黏土地基,厚度由数米到数十米不等,自地表而下红黏土含水量逐渐增大,干湿状态由坚硬、硬塑、可塑至软塑过渡。红黏土是一种特殊类黏性土,作为高速铁路的路基,其动力特性的研究显得更为重要。为此,作者以武广高速铁路工程为背景,利用自振柱试验仪研究了石灰类红黏土在动荷载作用下的动剪模量、阻尼比,分析了动剪应变幅值、围压对试验结果的影响,得到了红黏土的Gd/Gdmax～γd和λ～γd试验曲线及相应的拟合参数值,为红黏土路基动力稳定性评价及动力特性的深入研究提供了借鉴。

1 自振柱试验简介

根据扭转自由振动(自振柱)原理,采用自振柱试验仪进行扭转试验,测定土样的动剪模量 Gd和阻尼比 λ。试验原理及参数计算按我国现行规范《地基动力特性测试规范》(GB/T50269-97)及《土工试验规程》(SL237-1999)进行,此处不再详述。试验设备为南京工业大学岩土工程研究所研制的GZZ-1型自振柱试验仪[6],该系统由主机、气压管路、振动控制和测试 4部分组成,采用计算机控制试验过程及采集试验数据,具有良好的试验测试精度。试验所用土样为原状结构坚硬状态石灰岩类红黏土,取自武广高速铁路湖北泉口(DK 1294+50)附近,取样点离原天然地面分别为4.0m和7.5m。室内圆柱体试件尺寸为φ39.1× 80mm,原状结构红黏土物理指标平均值见表 1。本次试验方案主要考虑围压对动剪模量及阻尼比的影响,根据取样深度及重度计算竖向自重应力,围压按竖向自重应力的2/3取值,则深度4.0m处围压取为50 kPa,深度7.0m处围压取为100 kPa。

2 成果分析

2.1 动剪模量

为减小试验数据点的离散性,对动剪模量进行了归一化处理。如表 2所示,归一化动剪模量Gd/Gdmax随动剪应变的增大逐渐减小,变化曲线详见图1。如图1(a),红黏土Gd/Gdmax～γd曲线具有明显的非线性特征,不同围压下各试件归一化动剪模量随动剪应变的衰减趋势相似。当 γd＜10-4时,归一化动剪模量衰减速率相对缓慢,Gd/Gdmax～γd曲线近似呈线性变化,土样以弹性变形为主;当 γd＞10-4时,Gd/Gdmax随γd的增大迅速减小,衰减速率增大,Gd/Gdmax～γd曲线出现了明显的弯曲和方向偏转,土样以塑性变形为主。Gd/Gdmax～γd曲线的这种变化规律,间接地反映了红黏土动本构关系具有一般黏性土非线性、滞后性的规律。

表1 红黏土基本物理指标平均值Tab le 1 Physical indexes average value of red clay

表2 归一化动剪模量与动剪应变Tab le 2 Normalization dynamic shearmodu lus and dynam ic shear strain

为便于探讨围压对Gd/Gdmax～γd曲线变化规律的影响,分别取围压为 50、100 kPa时各试件归一化动剪模量平均值绘制Gd/Gdmax～γd曲线(见图1(b)),2曲线交点坐标为(γd≈2×10-4,Gd/Gdmax≈0.6)。当γd≤2×10-4、Gd/Gdmax≥0.6时,围压越大,动剪模量越大。因为随着围压的增大,试样孔隙比减小,相对密度增大,土颗粒接触点增加,土样刚度增大,使得应力波在土中的传播更快,从而增大了动剪模量,这一结果与文献[7-8]的研究结果一致。当γd≥2×10-4、Gd/Gdmax≤0.6时,出现了相反的情况,即同等条件下动剪模量随围压的增大而减小。因为当动剪应变水平较高时,动剪应变对动剪模量的影响大于围压对动剪模量的影响,即动剪应变增大引起动剪模量的减小量,大于围压的增大引起动剪模量的增大量。可见,动剪应变、围压对归一化动剪模量的大小均有明显的影响,当动剪应变水平相对较低时,围压对动剪模量的影响处于相对主要的地位,动剪应变的影响处于相对次要的地位;反之,当动剪应变水平较高时,动剪应变对动剪模量的影响掩盖了围压的影响,处于相对主要的地位。

对图1(a)中各曲线进行Davidenkov模型拟合,得到不同围压下红黏土的Davidenkov模型参数值。如表3所示:围压对参数 A,γ0的大小有明显影响,对参数B的大小有一定的影响,但不太明显;判定系数R2均在0.99以上,说明拟合效果良好。

表3 Davidenkov模型拟合参数Table 3 Fitting parameter values of Davidenkov Model

2.2 阻尼比

阻尼比反映动荷载作用下因土内阻损失能量的性质,是土动力特性的一个重要指标。不同动剪应变水平 γd对应的阻尼比 λ如表 4所示,λ～γd关系曲线详见图2。如图2(a)所示,红黏土阻尼比λ随动剪应变γd的增大非线性增大,同一围压(50 kPa或100 kPa)下3个试件对应的λ～γd曲线几乎重合,不同围压下的 2组曲线有明显不同。为了更好地分析围压对阻尼比变化规律的影响,在图 2 (b)中绘制了 2种围压下的平均曲线,两曲线的交点坐标为(γd≈2×10-4,λ≈10%)。当γd≤2× 10-4、λ≤10%时,围压越大,阻尼比越小;当 γd≥2×10-4、λ≥10%时,围压越大,阻尼越大。因为动剪应变水平较低时,它对阻尼比的影响相对较小,从而使围压对土样的加固作用得以表现出来;当动剪应变水平较高时时,动剪应变对阻尼比的影响掩盖了围压对阻尼比的影响。

表4 阻尼比与动剪应变Tab le 4 Dam ping ratio and dynamic shear strain

图2 不同围压下λ～γ关系曲线Fig.2 Relation curves ofλ～γd under different con fining pressure

如图 2所示,红黏土阻尼比 λ随动剪应变 γd变化规律比较复杂,用Hardin-Drnevich[10]模型和Davidenkov模型描述均有困难[11]。根据实测数据,从工程实用的角度出发,红黏土 λ～γd关系曲线可近似按经验公式(2)进行描述。式(2)中: λmax为红黏土最大阻尼比;m,n,γ0为拟合参数。按式(2)进行拟合,得到不同围压下各红黏土试件对应的最大阻尼比及拟合参数值。如表 4所示:本次试验所用红黏土最大阻尼比在19.9%～21.1%之间变化;判定系数R2均在0.98以上,说明拟合效果良好;围压对参数n,γ0的大小有明显影响,对参数m的大小有一定的影响,但不很明显。

表5 阻尼比经验公式拟合参数Table 5 Fitting parameter values of empirical formula of damping ratio

2.3 对比分析

为便于对比分析,将本次试验曲线与Seed和Idriss建议[12]的曲线范围一同绘制于图 3中。如图3(a)所示,红黏土Gd/Gmax～γd曲线位于文献[12]建议的饱和黏土曲线范围上边界线附近,二者变化趋势基本一致,红黏土动剪模量大于文献[12]建议的饱和黏土动剪模量平均值。红黏土作为一种特殊类土,具有不同于一般饱和黏土的物理力学性质特点,这可能是造成红黏土Gd/Gmax～γd曲线没有完全落在文献[12]建议的饱和黏土Gd/Gmax～γd曲线范围内部的原因之一。

如图3(b),红黏土λ～γd曲线位于Seed和Idriss(1970)建议[12]的砂土曲线范围上边界线附近,说明同等条件下红黏土阻尼比大于砂类土阻尼比的平均值。当γd＜7.0×10-5、λ＜6.5%时,红黏土 λ～γd曲线位于文献[12]砂土 λ～γd曲线范围上边界线的上方;当γd＞7.0×10-5、λ＞6.5%时,位于文献[12]砂土 λ～γd曲线范围上边界线的下方。因为当动剪应变小于某一值时,砂土的结构还没有产生液化破坏,红黏土阻尼大于文献[12]中砂土的阻尼比,这与黏性土的阻尼大于砂类土阻尼的结论是一致的;但随着动剪应变的逐渐增大,砂土因液化而丧失承载力,阻尼迅速增大,此时文献[12]中砂土的阻尼大于坚硬状红黏土的阻尼值。

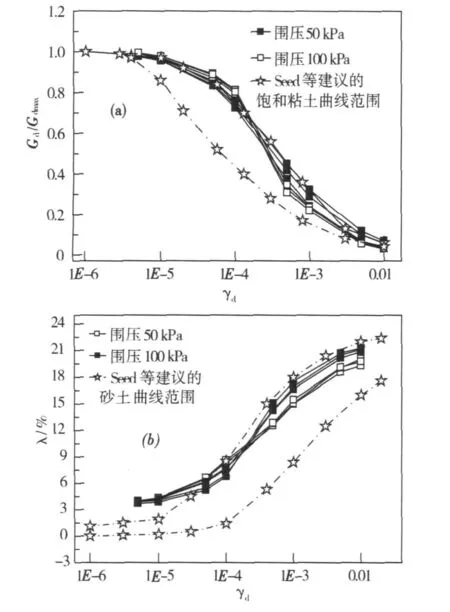
图3 试验曲线与文献[12]建议的曲线范围Fig.3 Test curves and curve range suggested by ref.[12]

3 结 论

(1)获得了2种围压下红黏土的Gd/Gdmax～γd及λ～γd曲线,给出了红黏土Davidenkov模型参数、λ～γd曲线的经验公式及相应的拟合参数。

(2)动剪应变、围压对红黏土动剪模量及阻尼比具有明显影响。不考虑其它因素的影响,动剪模量随动剪应变的增大非线性减小,阻尼比随动剪应变的增大非线性增大。围压对红黏土动剪模量、阻尼比的影响与动剪应变水平有关:动剪应变幅小于2×10-4时,围压越大,动剪模量越大,阻尼比越小;反之,动剪应变幅大于 2×10-4时,围压越大,动剪模量越小,阻尼比越大。

(3)对比分析表明,红黏土动剪模量大于一般黏土动剪模量平均值,红黏土阻尼比大于一般砂土阻尼比平均值。

[1]孙 静,袁晓铭.土的动模量和阻尼比研究述评[J].世界地震工程,2003,19(1):262-264. SUN Jing,YUN Xiao-ming.A state-of-art of research on dynamic modulus and damping ratio of soils [J].World Earthquake Engineering,2003,19(1):262 -264.

[2]陈国兴,刘雪珠,朱定华,等.南京新近沉积土动剪切模量比与阻尼比的试验研究[J].岩土工程学报, 2006,28(8):1023-1027. CHEN Guo-xing,LIU Xue-zhu,ZHU Ding-hua,et al.Experimental studies on dynamic shear modulus ratio and damping ratio of recently deposited soils in Nanjing [J].Chinese Journal ofGeotechnical Engineering,2006, 28(8):1023-1027.

[3]CHEN Guo-xing,ZHU Ding-hua.A study on dynamic shearmodulus ratio and damping ratio of recently deposited soils for southern region of Jiang-su Province along Yangtze river,China[C]//Proceeding Fourth International Con ference on Soft Soil Engineering,Vancouver,Canada,London:Taylor and Francis Group,2006.

[4]Jianfeng Z,Ronald D A,Juang C H.Normalized shear modulus and material damping ratio relationships[J]. Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2005:453-464.

[5]吕悦军,唐荣余,沙海军.渤海海底土类动剪切模量比和阻尼比试验研究[J].防灾减灾工程学报,2003,23 (2):35-42. LU Yue-jun,TANG Rong-yu,SHA Hai-jun.Experimental study on dynamic shearmodulus ratio and damping ratio of the soils of Bohaiseafloor[J].Journalof Disaster Prevention and Mitigation Engineering,2003,23 (2):35-42.

[6]陈国兴,朱定华,何启智.GZZ-1型自振柱试验机研制与性能试验[J].地震工程与工程振动,2003,23 (1):110-114. CHEN Guo-xing,ZHU Ding-hua,HE Qi-zhi.Development and property tests of GZZ-1 free vibration column test system[J].Earthquake Engineering and the Engineering Vibration,2003,23(1):110-114.

[7]Silver M L,Seed H B.Volume changes in sands during cyclic loading[J].Journal of the Soil Mechanics and Foundation Division,ASCE,1971,97(9):1171-1182.

[8]Flores O C,Romo M P O.Dynamic behavior of Tailings [C]//Proc of Fourth InternationalConference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamic and Symposium in Honor of Professor Liam W D Finn San Diego,California:2001:1-6.

[9]Hardin BO,Drnevich V P.Shearmodulus and damping in soils design equation and curves[J].Journal of Soil Mechanics and Foundation,ASCE,1972,98(SM 7): 603-642.

[10]Martin P P,SEED H B.One dimensional dynamic ground response analysis[J].Journal of Geotechnical Engineering,ASCE,1982,108(7):935-954.

[11]陈国兴,谢君斐,张克绪.土的动模量和阻尼比的经验公式[J].地震工程与工程振动,1995,15(1):73～84. CHEN Guo-xing,XIE Jun-fei,ZHANG Ke-xu.The empirical of soilmodulus and damping ratio for dynamic analysis[J].Earthquake Engineering and Engineering Vibration,1995,15(1):73-84.

[12]Seed H B,Id riss IM.Soilmodulus and damping factors for dynamic response analyses,Report No.EERC 70-10[R].Earthquake Engineering Research Center,University of California Berkeley,1970.