沅水流域径流演变规律研究
王顺强 胡国华
(湖南省防汛抗旱指挥部办公室长沙市410007)(长沙理工大学长沙市410015)
1 绪论
径流是地球表面水循环过程中的重要环节,它的化学、物理特性对地理环境和生态系统有重要的作用。径流在国民经济中具有重要的意义,是构成地区工农业供水的重要条件,是地区社会经济发展规模的制约因素。径流受地貌、气候、土壤、植被等自然条件以及人类活动等因素的影响,当其中某种条件发生了变化,径流就会表现出一定的变化趋势,径流演变过程既表现出确定性的规律,同时也具有一定的随机性。径流特征的变化不仅影响水资源的开发利用,同时也影响着社会经济的发展。分析径流的演变过程,认识演化的规律和动因,不仅有可以深入了解水资源的变化特征,为水资源的合理开发利用提供有利依据,同时也有利于开发过程中的总体协调和控制。
沅水俗称沅江,是洞庭湖水系中仅次于湘江的第二大河流。沅水发源于贵州东南部,有南北二源,以南源为主。国内外学者对流域降雨径流长期演变规律开展了大量研究工作,而沅水流域有关这方面的研究较少,有关沅水流域水资源量演变规律方面的研究目前开展较少。吴作平[1]根据滤波相关理论对沅水流域近81年径流序列资料进行分析,分析了周期性规律,得出了对序列影响最大的周期分别为16.7年、5年的结论。黄斌[2]用1994~2003年沅江中上游水质监测数据,采用单因子分析法、主成分分析法、季节性肯达尔检验等方法对该流域水质进行了综合评价,同时探讨了人工神经网络在水环境质量评价中的应用。本文将对自然变化和人类活动双重影响下的沅水流域径流长期演变规律进行分析探讨,为流域防洪、抗旱以及水资源和水能资源开发利用等提供科学依据。
2 研究数据及方法
本文选取沅水流域代表站安江站、浦市站以及桃源站的年平均径流量进行流域的年径流演变规律分析,进而揭示沅水流域径流的年际变化规律。分析内容包括三个代表站径流量的变异性分析及趋势性分析,变异性分析采用累积距平曲线联合T检验法,趋势性分析采用SRST模型法。
2.1 分段线性回归(SRST)方法
分段线性回归(SRST)方法(Segmented Regression SystemoverTime)是由Shao和Campbell于2002年提出的[3]。该方法在不知道趋势分段及变点位置的情况下,可同时检测出序列的趋势和突变。因此,分段线性回归模型看做是检测变点和趋势分析的两种目的兼容的方法。这个模型定义了三类点:变点(跳跃性变化)、拐点、结点。变点被定义为线性趋势和周期趋势变化同时可能使序列不连续的点;拐点是指线性趋势变化但是满足连续条件的点;而节点是指周期趋势变化但仍连续的点[4]。通常,线性回归方程可以写成以下形式:

分段线性回归模型是在找出序列中的变点基础上把序列分成各个子序列,然后按照序列的增长或减少的趋势分段进行线性模拟。建立分段线性回归模型的步骤如下:
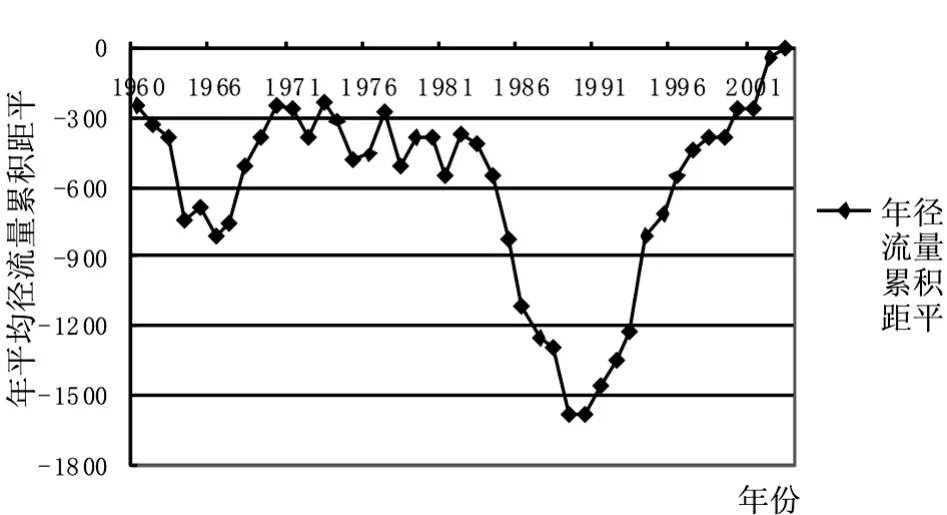
①对于一组将序列分成L+1个子序列的具有L个变点变异点集r1 其中R0=0、rL+1=∞;{ul(t})代表各个子序列的线性回归方程。 ②当用线性回归分别模拟各个子序列趋势时,由于子序列中存在增大或减小的趋势,用线性方程模拟时需要对子序列分段进行模拟,而拐点就是进行线性模拟时斜率变化的点。假定序列在变点rl-1与rl之间的第l个子定义为: 其中Jl,0=r-1;(t-Jl,k)+=u+被定义如下式 ③SRST方法采用最小二乘法来进行模型的拟合。即模型的参数,包括变点和拐点的数量及位置,不同分段的回归系数和截距,以及残差的平方和等,都是通过残差平方和的最小化来进行拟合的,表达式如下: 在SRST模式识别中,由Hurvich与Tasi改进的AIC准则(AICc)被用来确定模型中变点和拐点的最优数量和位置,而最小二乘法则用于模型的优选。AIC准则是通过RSS数值和模型中的自由参数的数量来建立的,其表达式如下: 其中N是序列观测值的个数,p是模型中独立的参数的个数。在第L个子序列中相互独立的参数,因此,整个序列独立的参数的数量可以看成: 优选模型可通过AICc的最小化来实现。 在分段线性模型中确定变点和拐点的位置十分关键。原理上,所有不同的变点和拐点的组合可以用适当的准则来选取最优的结果。然而,在实际的计算中这样的组合的数量很多,利用准则来优选就很不实际。所以,可以先通过一些方法来确定变点和拐点并结合准则来确定。下面介绍识别变点和拐点的方法。 目前,对序列的变异性分析大多都运用了大量的统计公式,方法较为复杂,本文运用一种较为简单直观的方法进行变点识别,即累计距平曲线-滑动T检验联合识别法。用累计距平曲线法对变点做初步诊断,找出变异点,再利用滑动t检验法进行精确识别。 累计距平曲线法原理: 累积距平是一种常用的判断变化趋势的方法。对于水文样本序列x1,x2……xn,在某一时刻t的累积距平表示为: 点绘出St~t曲线,可进行初步变点分析。 滑动t检验法: 对已知的年径流样本序列x1,x2……xn,选定某一年份,分别取其前和后相邻的连续n1和n2年的年径流量值计算统计量T值。其中和s1、s2分别为前后n1年和n2年的均值和标准差。 累积距平曲线-滑动t联合检验: 根据累积距平曲线法与滑动t检验的原理,累积距平曲线-滑动t联合检验的过程为: (1)变点的初步识别。 利用公式(1-8),以St为纵坐标,t为横坐标得到累积距平曲线图,从图中找出St的最大值和最小值,假设它们所对应的横坐标为可能的变点。 (2)变点的精确识别。 对初步识别得到的变点利用滑动t检验法进行精确识别。先利用公式(9)出统计量T的值,再以置信度α=0.05,自由度n=n1+n2-2查t分布表得到Tα/2值。将Tα/2值与计算出的统计量T值进行比较,当|T|>Tα/2时,表明年径流量序列在该点存在显著性变异,该点为变点,反之该点不是变点。 总体上来看,用该方法识别变点避免了复杂的统计公式的运用,只需对累积距平曲线的最值进行精确的变点识别,避免了对整个序列点做变点假设,识别过程简便明了,且通过图表来找变点比较直观。 拐点被定义为线性趋势变化但仍连续的点,是指分段线性模拟时斜率变化的点,本文将在绘制径流过程线基础上,结合径流总体趋势选取拐点,最后再通过AIC的最下值来确定最优拐点。 利用公式(8)分别以安江、浦市和桃源三站的年平均径流量累积距平为纵坐标,年份为横坐标得到年平均径流量累积距平曲线图,结果见图1~图3。 图1 安江站年平均径流量累积距平曲线图 图2 浦市站年径流量累积距平曲线图 图3 桃源站年径流量累积距平曲线 从图1以看出,安江站年平均径流量累积距平曲线最小值出现在1990年,最大值出现在2003年以后,因资料长度限制无法确定最大值出现的年份,故初步选取1990年为安江站年平均径流量的变异点。从图2可以看出,浦市站年平均径流量累积距平曲线的最大年份为1970年,最小年份为1990年,因年平均径流量资料长度的限制,无法判定1970年是否为变异点,故初步选取1990年为浦市站年平均径流量的变异点。由图3可以看出,桃源站年平均径流量最小值年份为1963年,最大值年份为2004年,因年内平均径流量资料长度的限制,初步选取次小值年份1990年、次大值1977年为变异点。 分别对累积距平曲线法初步确定的三个站的变异点运用滑动T检验法进行精确识别,检验结果见表1。 表1 沅水流域年平均径流量滑动T检验表 对于安江站,在1990年前取10年(1980~1989年)和后取10年(1990~1999年),分别计算出=711.53 mm,=950.44 mm,S1=145.52,S2=121.08,代入公式计算得S=133.86,T=-3.99。因为|T|>Tα/2=2.1,故否定原假设H0:=0,说明其存在显著性差异,即安江站年平均径流量该点(1990年)发生均值突变。对于浦市站,同样在1990年前后各取连续10年,计算出=1 005.06 mm,=1 452.35 mm,S1=185.86,S2=382.60,代入公式计算得S=300.77,T=-3.33。因为|T|>Tα/2=2.1,故否定原假设H0:=0,说明其存在显著性差异,即浦市站年平均径流量该点(1990年)发生均值突变。桃源站存在两个初估变异点1977年和1990年,分别在其两点前后各取连续10年,计算出T1977=0.99,T1990=-0.86。因|T1977| 通过累积距平曲线法初步识别安江站、浦市站的突变点均为1990年,桃源站突变点为1977年和1990年。对初步识别的突变点用滑动T检验法精确识别结果得出:安江站、浦市站的年平均径流量序列在1990年发生均值突变,桃源站年平均径流量未发生均值突变。 选取安江站1960~1990年的年径流资料、浦市站1966~2003年的年径流资料和桃源站1960~2008年的资料进行沅水流域的年径流趋势性分析,分析方法采用SRST模型。 如前文所述,安江站与浦市站的年径流变异点位1990年,而桃源站没有检测到变点。安江站的拐点选取为1969年、1984年和1998年,浦市站的拐点选取为1972年、1985年和1999年,桃源站的拐点选取为1970年、1989年和2002年,具体计算结果见表2。 表2 年径流量分段线性回归分析统计表 从模型回归表2中可以看出在变点之前,安江站年径流经历了一个上升又下降的过程。1960~1969年每年增大约33.7 m3/s,而在1969~1984年呈下降趋势,平均每年下降约51.7 m3/s,1984~1990年每年上升约44.1 m3/s。在变点之后,径流量呈先下降后又上升的趋势,1990~1998年平均每年下降20.1 m3/s,1998~2003年平均每年上升29 m3/s。在变点之后浦市站的年径流呈先上升后下降的趋势,1990~1999年平均每年上升59.6,而在之后年径流平均每年下降211.7。从模型回归表2中可以看出,桃源站的年径流量总体的趋势时先上升后下降,然后再上升再下降的一个过程。1960~1970年平均每年约上升45 m3/s,1970~1989年平均每年下降66 m3/s,1989~2002年平均每年上升28 m3/s,而在2002年之后平均每年下降163 m3/s。 从流域的总体趋势上看,三个站在1990年之前大致都有一个先上升后下降之后又上升的过程,但各个站点的拐点不相同。在1990年之后,桃源站呈先上升后下降的过程,浦市站是先上升后下降的过程,而安江是先下降后上升的过程。 通过对沅水流域代表站年平均径流变异性分析,得到安江站、浦市站的年平均径流量序列在1990年发生均值突变,桃源站年平均径流量未发生均值突变,而安江站与浦市站在1990年之后年径流序列的均值有显著的增大。利用SRST模型进行趋势分析得到:安江站年径流在变点之前经历了一个先上升后下降的过程;在变点之后,径流量呈先下降后又上升的趋势。浦市站径流在变点之前总体呈先下降后上升的趋势;在变点之后呈先上升后下降的趋势。桃园站的年径流量总体的趋势是先上升后下降,然后上升再下降的一个过程。从流域的总体趋势上看,三个站在1990年之前大致都有一个先上升后下降,之后又上升的过程,但各个站点的拐点不相同。在1990年之后,桃源站和浦市站均呈先上升后下降的过程,而安江呈先下降后上升的过程。 本文的研究还有一些问题尚待解决,还需进一步深入研究: (1)变点的选取在SRST模型运用中十分关键,本文应用的是一种简洁、直观的方法,而与其他变点分析方法的比较有待进一步展开。 (2)拐点的选取影响着SRST模型的拟合效果,以后研究中应该注重探索更为简便和精确的方法。 (3)本文是根据流域径流历年来实测资料进行趋势分析,还需深入研究采用适当的方法进行水文情势未来变化趋势预测的研究。 1 吴作平.沅水流域径流周期性规律分析[J].水电能源学,2009,8(4):16-18. 2 黄斌.人工神经网络在沅江中上游水环境质量评价中的应用研究[D].湖南大学,2006. 3 Shao QX,Campbell NA.Modelling trends in groundwater levels by segmentedregressionwithconstraints[J].Aust NZ J Stat,2002,44:129-141 4 Quanxi Shao,Zhanling Li,and Zongxue Xu.Trend detection in hydrological time series by segment regression with application to Shiyang River Basin[J].Stochastic Environmental Research and Risk Assessment,2009,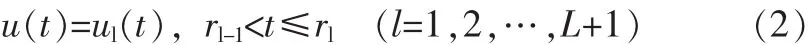
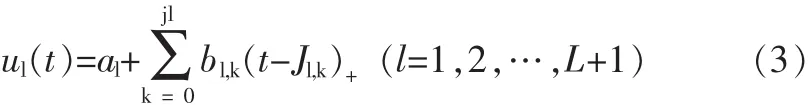

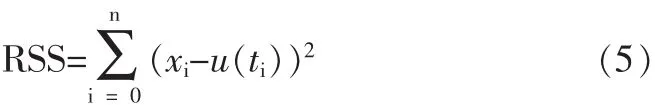
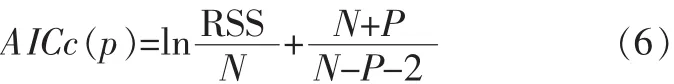
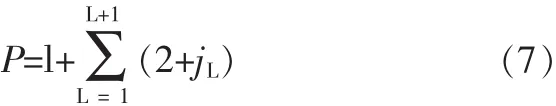
2.2 累积距平曲线-滑动t检验联合识别变点法
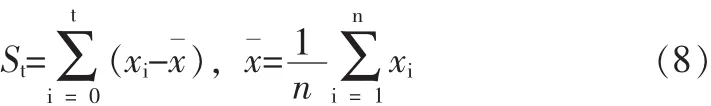
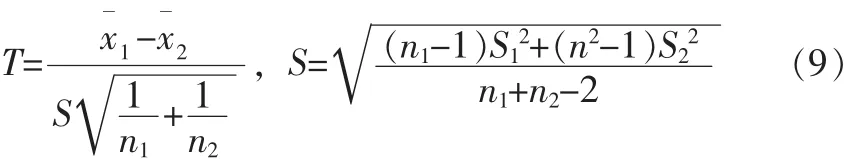
3 径流变异性分析
3.1 变异点的初步识别
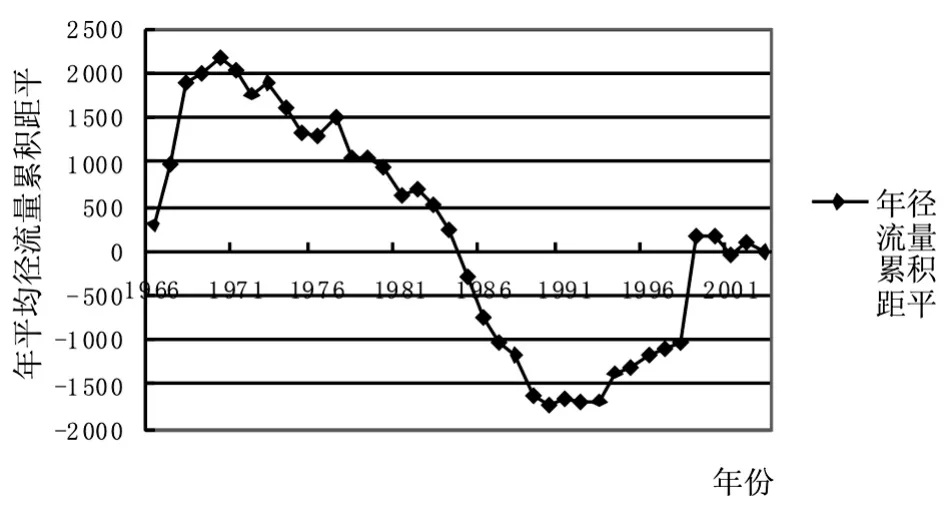
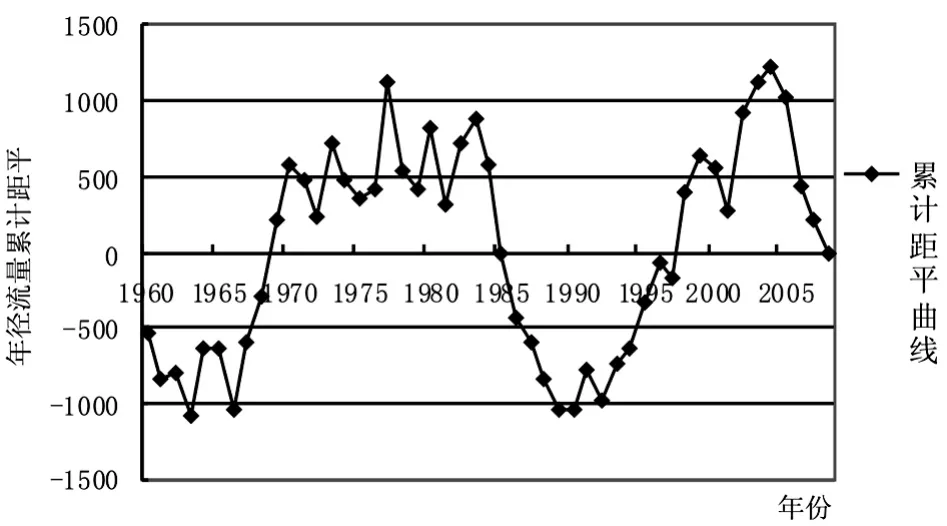
3.2 变异点的精确识别
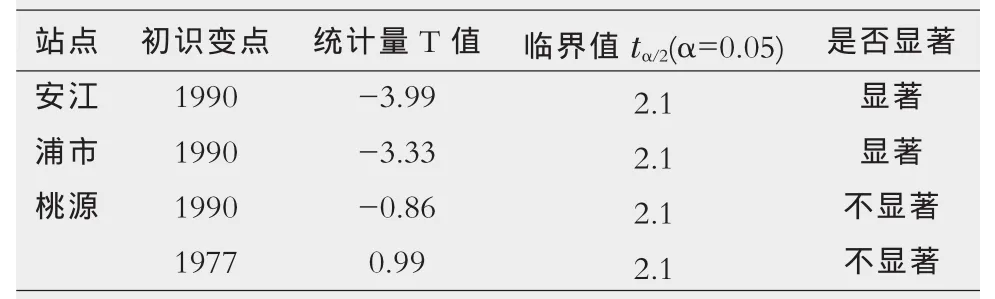
3.3 小结
4 径流的趋势性分析
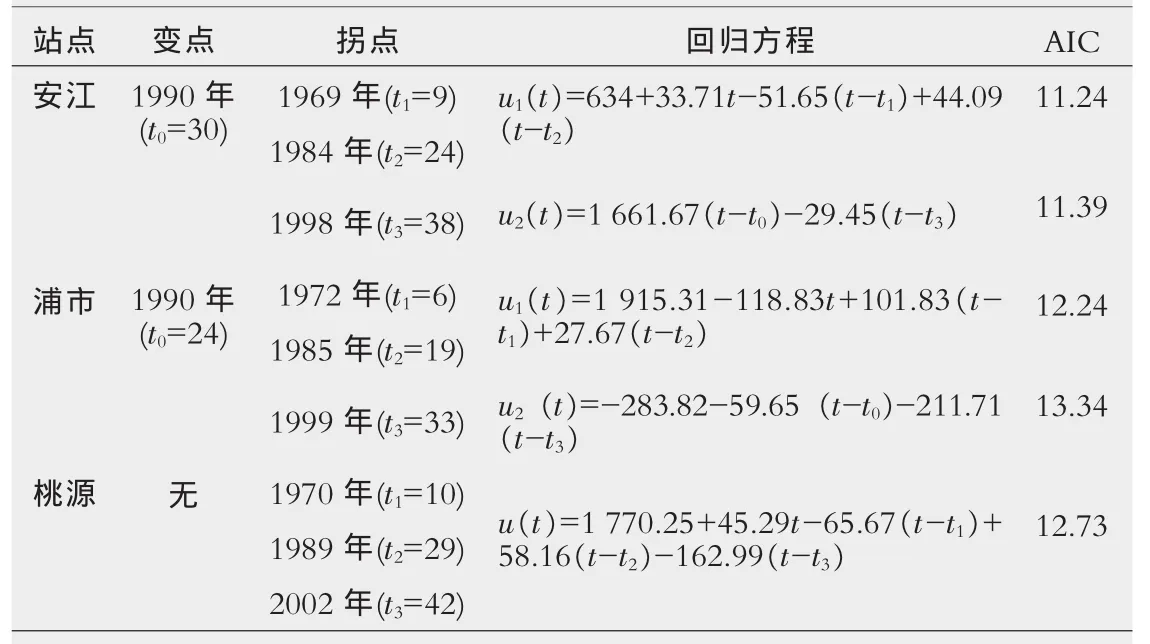
5 结语


