浅谈折线形墙背的土压力计算

王世强,李长松

(黑龙江省龙建路桥第四工程有限公司)

1 上墙土压力计算

凸形墙背的挡土墙和衡重式挡土墙,其墙背不是一个平面而是折面,称为折线形墙背。对于这类墙背,以墙背转折点或衡重台为界,分成上墙与下墙,分别按库仑方法计算上下墙的主动土压力,然后取两者的矢量和作为全墙的土压力。

计算上墙土压力时,不考虑下墙的影响,凸形墙背上墙按俯斜墙背计算其土压力。衡重式挡墙的上墙,由于衡重台的存在,通常将墙顶内缘与衡重台外缘的连线作为假想墙背,假想墙背与实际墙背间的土楔假设与实际墙背一起移动。计算土压力时先按墙背倾角 α或假想墙背顷角α′是否大于第二破裂面倾角αi,判断是否出现第二破裂面,如果出现第二破裂面,按第二破裂面的主动土压力公式计算作用于上墙的土压力,如果不出现第二破裂面,以实际墙背或假想墙背为边界条件,按一般直线墙背库仑主动土压力计算。

2 下墙土压力计算

2.1 延长墙背法

如图 1所示,在上墙土压力算出后,延长下墙墙背交于填土表面C,以B′C为假想墙背,根据延长墙背的边界条件,用相应的库仑公式计算土压力,并绘出墙背土压力分布图,从中截取下墙BB′部分的应力图作为下墙的土压力。将上、下墙两个部分的应力图叠加,即为全墙土压力。

图1 延长墙背法

这种方法存在着一定的误差。第一,考虑了在延长墙背与实际墙背上土压力方向不同而引起的垂直分力差,但忽略了延长墙背与实际墙背间的土楔及荷载重,两者虽然能相互补偿,但未能相互抵消;第二,绘制土压力应力图形时,假定上墙破裂面与下墙破裂面平行,但多数情况下两者是不平行的,由此存在计算下墙土压力所引起的误差。由于以上误差一般偏于安全,且计算简便,此法至今仍被广泛采用。

2.2 力多边形法

在墙背土体处于极限平衡条件下,作用于破裂棱体上的力系,应构成闭合的力矢量多边形。在算得上墙土压力 E1后,就可以绘出下墙任一破裂体的力多边形来推求下墙土压力,这种方法叫力多边形法。

现以路堤挡土墙下墙破裂面交于荷载范围内的边界条件为例,介绍多边形法计算下墙土压力的公式推导。

在极限平衡条件下,破裂棱体AOBCD的力多边形为abed,其中abc为上墙破裂棱体AOC′D的力平衡三角形,bedc为下墙破裂棱体C′OBC的力平衡多边形。eg∥bc,cf∥be,gf =ΔE。在Δcfd中,由正弦定理可得

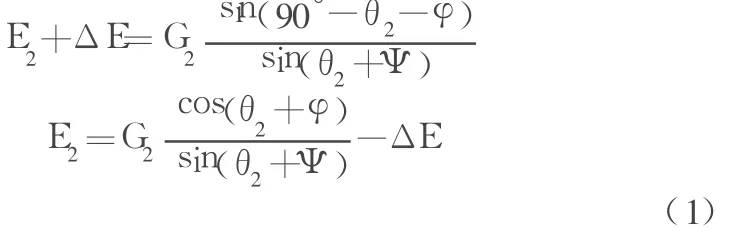
挡土墙下部破裂棱体重量G2为

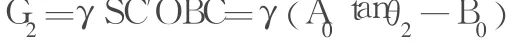
其中

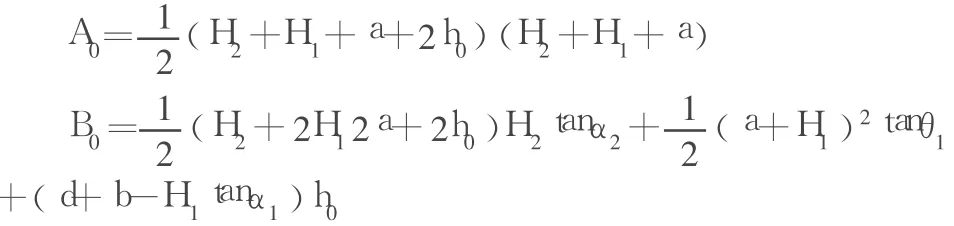
在Δefg中,有

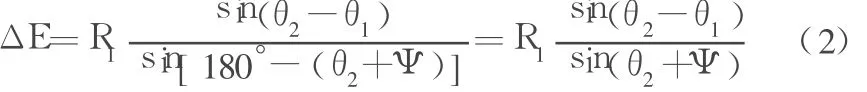
在Δabc中,上墙土压力已经求出,则

将G2及ΔE及代入(1),得

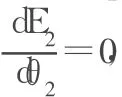
把求得的破裂角 θ2代入式(4),即可求得下墙土压力E2。

在作用于下墙的土压力图形(图 2)中,可以近似假定θ1≈θ2,即

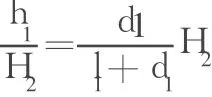
则

土压力作用点为