用累积地震矩法研究全球地震活动性*

侯燕燕 张晁军

（中国地震台网中心，北京 100045）

用累积地震矩法研究全球地震活动性*

侯燕燕 张晁军

（中国地震台网中心，北京 100045）

本文基于Lomnitz提出的MRI理论，用“累积地震矩（CSM）”算法对全球1900—1999年7级以上的地震进行了处理，试图通过分析大震前CSM图像的变化，来判断地震发生的可能性。对不同地区的6个地震震前CSM图像的分析表明：7级以上地震的CSM图像在震前5到10年内会改变，大部分地震发生在CSM的高值区或次高值区。通过实际运算发现：在不同的地区应使用不同的值可获得较好的结果，用于计算的地震数越多，获得的结果越好。有些大地震前CSM异常区域不是唯一的，往往会出现几个，这可能与研究区域的地震活动性有关。因此，笔者认为：若要获得可靠的CSM图像，除应当考虑不同地区的小震活动水平外，还应考虑地震断层对震后能量分布影响。统计结果表明：在目标地震发生后，下一次地震在空间上发生在原地及2度距离范围内的概率较大，在3度以外区域发生的概率相差不大；在时间上，发生在原地区震后1年内的概率最高，这可能与余震活动有关；在5年的时间里，下一次地震发生的次数占到全部地震的70%以上。因此，要注意大地震后，目标地震附近有地震能量进一步释放的危险性。

累积地震矩；7级以上地震；下一次地震

引言

众所周知，地震预报仍然处于探索阶段，许多学者尝试不同的路径，采用多种方法和观测手段试图在这方面取得突破性的进展。地震空区就是其中方法之一［1-2］。然而，基于地震空区的经验技术很难进行定量化，并且对空区是否有进一步破裂的可能性看法不一：一种观点认为地震空区是潜在的破裂区；另一种观点则把地震空区看作是无震区，不能产生大地震。可是，大部分大震继续在地震空区内发生。板块边界的许多段，也许是大部分，已被人指定为地震空区。大震的发生可能同这个事实有些关系。另一方面，一些学者认为：被指定为有发生最大地震可能性的空区和主震的位置几乎没有什么联系［3］。就目前的状态而言，很难避免类似对地震空区模棱两可的解释。

许多地震学家试图将地震空区定量化，以解决上述问题。其中之一是1993年Lomnitz提出的矩比成像法MRI（Moment Ratio Imaging），即通过检验大震前MRI图像的变化，来预测未来大地震发生的位置［4-5］。黄建平等［6］首次用该算法分析了1966年以来中国不同地区7.0级以上地震前震中及其周围MRI值对应的异常演化过程，发现通过分析MRI值异常的时空变化，能够定量化确定未来大震的空间范围和时间迫近程度，并认为MRI值的时空变化能够定量反映大震发生的时空要素，而且MRI值的变化特征能够反映介质破裂的规律。Zhang Chaojun等［7］用MRI方法对板块边界的地震周期进行了探讨，认为MRI值可作为活动构造区能量消散和汇聚的指示器。本文基于Lomnitz提出的MRI理论，用“累积地震矩”算法对全球1900—1999年7级以上地震进行了处理，选了其中的6个地震作为范例，通过分析大震前累积地震矩图像的变化，对下列问题有所解答：CSM在大震前总是有所变化吗？CSM是可靠的地震前兆信号吗？如果是的话，那么在大地震前多大的范围内能检测到这样的前兆？

1　累积地震矩CSM的基本原理

墨西哥地震学家Lomnitz l993年提出伤口愈合的概念——累积地震矩法来研究地震空区。其基本原理如下：假定在t＝0时刻发生了一个地震，地震矩为M0，那么下一次发生在同一个地方地震的概率将随着时间t而增加。假设该破裂的愈合速度，就像伤口表皮的愈合速度一样，在任何时候都是与未愈合区的面积成比例的，则可以用下面的方程表示板块边界的愈合过程：

其中m0是经过t年后未愈合的地震矩，M0表示第一个地震的初始时刻地震矩，t是研究的时间步长，τ表示第一个地震的地震矩M0的半周期。数值常量ln（1/2）＝－0.69315是半衰期因子，在t＝0时，m0＝M0；t＝τ时，m0＝M0/2。在板块边界，τ＝20年［4］。不同地区τ值不同，由于半衰期与地震复发周期之间存在一定的比例关系，通过古登堡-里克特的震级-频度（G-R）关系，计算地震周期TM，根据得到的不同震级的复发周期值TM得到不同震级的半衰期［6］。方程（1）描述的是在一个孤立段的情形。地震的发生不是孤立的，是受到构造体系内部以及构造块体之间的各种作用下产生的，一次地震的产生也必将在周围地区产生影响，表达这种影响的形式之一是把地震矩M0在震中周围一定范围内，按照某个原则进行分配。那么，假设后续地震是某一个地震矩异常在时空上线性迭加的结果，则可以得到某一个地区的累积地震矩。在给定的任一地区，都有方程：

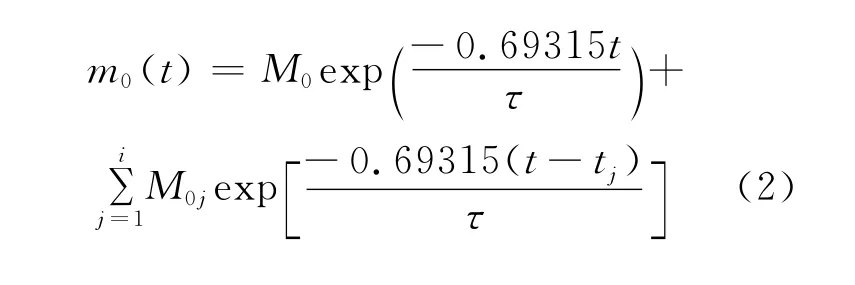
这里［M01，t1］，［M02，t2］，…［Moi，ti］是在（0，t）内该区域内的地震。m0是方程（2）计算出来的累积愈合地震地震矩。

可以进一步假定：固定破裂区的影响随距离指数衰减，在距离超过17倍的断层长度时，影响可以忽略不计。这里说的断层长度是1992年6月28日加利福尼亚州兰德斯市7.3级地震触发小震的距离，大约为100 km左右。

在空间上计算累积地震矩时，断层区被分成许多单元。以震中为中心8°×8°区域作为研究区域，以1°×1°区作为单元网格，采用墨西哥帽模型［8］对每个单元进行累积地震矩分配：在［－3°～3°］区，被认为是能量集中区，故填充60%的累积地震矩分布，在［－5°～－3°］和［3°～5°］区，被认为是转换区，聚集能量较少，填充地震矩分布10%的累积地震矩分布，在［－8°～－5°］和［5°～8°］区，被认为是地震触发区，填充20%的累积地震矩的分布，地震在空间释放10%的累积地震矩的分布。在考虑地震矩分布时，忽略模型沿弧型构造带走滑断层的影响，并认为地震矩的分布在震中两侧是均匀分布的，不考虑地层结构的复杂性和岩石介质的横向不均匀性。

2　CSM模型研究的区域

根据这一原理我们分析了1900—1999年全球7级以上的浅源地震目录（震源深度小于60 km），编程处理了哥伦比亚l979年12月12日MW8.1地震、墨西哥1985年9月19日MW8.0地震、日本千岛群岛1994年10月4日MW8.3地震、印尼伊里安查亚1996年2月17日MW8.2地震、土耳其伊兹米特1999年8月17日MW7.6地震和美国迪纳利2002年11月3日MW7.9地震，详见表1。初始空间能量分布是从研究区域第一个地震的地震矩开始分配，截至目标地震前2年为止，目的是看这一地区是否存在累积地震矩高值，也就是这一地区是否危险。

3　计算和结果分析

在CENT.CAT目录中选了6个大于7.5级的地震作为CSM计算的例子，表1列出了每个地震的详细信息。在计算前我们对每一地区的地震活动性进行了分析，并经验地获得了每一地区的τ。图1—6是每个地震前的图像。左边的彩图是在［－8°～8°］区域内CSM异常分布云图。彩色条表示CSM异常值的大小。Dt表示时间步长，或计算CSM的结束时间：即从1900年以来在Dt时间内CSM的变化，Dt总是小于目标地震时间。X轴是经度；Y是纬度。红点表示震中位置。右边的图是Dt年内不同研究区域的M＞7地震分布图。T0表示目标地震的发震时间。

根据结果来看，6个地震中的5个几乎都发生在CSM的高值区或次高值区。只有第6个地震偏离了异常区。很明显，在迪纳利地区M＞7级地震偏少，有理由认为这种现象大概与当地的地震活动性和地质构造有关。同样，在这个例子的高值区，目标地震没有发生。难道这些是假异常？查看CSM高值区在Dt后的地震目录就会发现在CSM高值区地震活动性会增强。

4　CSM可靠性和下一次地震在时间空间上发生的概率

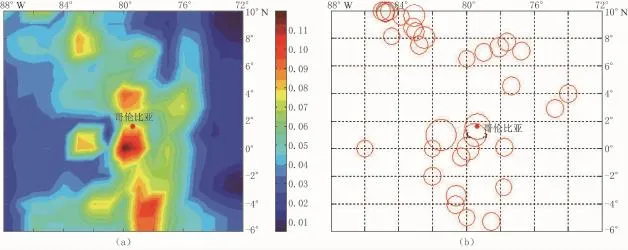
图1　（a）Dt=77 a，τ=20 a；T0：1979-12-12；（b）哥伦比亚（1900—1979年）的地震分布

图2　（a）Dt=83 a，τ=20 a；T0：1985-09-19；（b）墨西哥（1900—1985年）的地震分布

图3　（a）Dt=92 a，τ=25 a；T0：1994-10-04；（b）千岛群岛（1900—1994）的地震分布

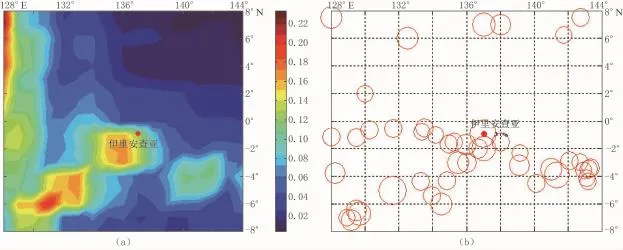
图4　（a）Dt=94 a，τ=18 a；T0：1996-02-17；（b）伊里安查亚（1900—1996）的地震分布

图5　（a）Dt=92 a，τ=15 a；T0：1999-08-17；（b）土耳其伊兹米特（1900—1999）的地震分布

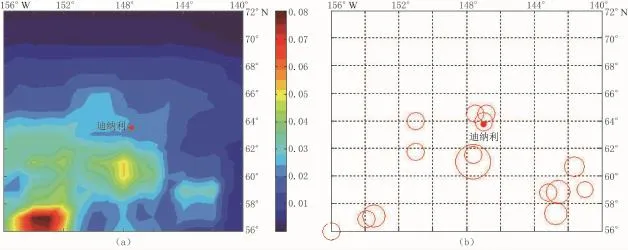
图6　（a）Dt=100 a，τ=30 a；T0：2002-11-03；（b）迪纳利（1900—2000）的地震分布

按照上述的分析，CSM的图像在大震前将会改变。地震将会发生在CSM的高值区或次高值区。在某种可接受的时间-空间范围内很有必要对CSM算法的有效性进行统计以证明这种算法的可靠性。不过要注意这样的统计试验不支持CSM算法想把地震空区定量化的假说。其原因不难理解，CSM算法是以某一地区大震（M＞7）数据为基础，并且忽略模型沿弧型构造带走滑断层的影响，并认为地震矩的分布在震中两侧是均匀分布的，不考虑地层结构的复杂性和岩石介质的横向不均匀性。但是，它们的发生率在任何给定的时间间隔范围内，因不同的地区而变化很大。在很少发生7级地震的地区，地震矩缺陷不能被计算，则地震发生前，CSM变化不明显。最终这可能有利于用小地震来计算CSM。这种做法可能对多地震地区结果较好，在那里存在相当可靠的M＞4数据。另一方面，因为小地震事件的探测水平，尤其是在1960年之前很不均匀，故这种方法不能在世界范围内被推广应用。当取样数据的完整性在空间、震级和时间上强烈改变时，没有可靠的统计方法处理小震序列。总之，目前新技术的全面成功率还不能从统计学角度来评价。

另外，大致合理的结果需要对地震的震源机制、破裂区所达到的最远距离或应力传输的范围有所了解。我们只提供了一个简单的震后地震矩的分布模型，显然，这不足以获得好的结果。为了更好地了解这个问题，我们对1900—1999年期间，每个7级以上地震在震中至距震中10度区域内发生的下一次地震的时空分布进行了统计，见图7、8。

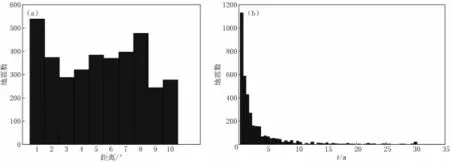
图7　（a）1900年至1999年期间，距震中10度区域内发生下一个地震的次数统计。X轴表示距离，单位：度。Y轴表示地震数。柱状图表示每一度区下一次地震发生的多少。在1到8度区内发生下一次地震的次数要高于其他区。在2、5、6、7度区内发生下一次地震的概率基本相同。在3、4、9、10度区内发生下一次地震的概率较低。这个结果在具体的地区将有所不同。因此，CSM模型很难适合每一个研究地区，模型应该根据不同的研究区域进行修改。（b）在30年期间下一次地震发生的概率。数据是从1900年至1999年。X轴表示时间，单位：年。Y轴表示地震数。柱状图表示每一年地震发生的概率。此图显示目标地震之后发生地震的概率将指数衰减。其中大部分地震将在3年内发生。因此，每次7级以上地震的发生在若干年内都会引起全球地震活动性的增强。而这种地震的发生以距震中100 km和800 km左右复发的概率最大

5　结论

以上的分析表明：7级以上地震的CSM图像在震前5～10年内会改变，可是难于判断地震的具体位置。在不同的地区应使用不同的值来获得较好的结果。CSM方法可用来研究全球M＞7地震活动性。在计算CSM的过程中，CSM异常区域不是唯一的，往往会出现几个，这可能与研究区域的地震活动性有关。用于计算的地震数越多，获得的结果越好。另外，应当考虑不同地区的地质构造因素来检验不同的地震矩分布模型。在时间和空间上，在上述所谈的余震区和触发区，发生下一次地震的概率较高。在15年左右时间内，下一次地震发生的次数呈指数分布。如果考虑在每单位面积内下一次地震发生的概率，则在1～2度距离范围内概率分布最高，分别达到了16%和14%。在其他距离上，下一次地震发生的概率几乎相等。

图8　单位面积内下一次地震发生的概率。X轴表示距离，单位：度。Y轴表示在每一度面积内发生下一次地震的概率大小，以柱状图来表示。图中显示了1～8度距离范围内的下一次地震发生的概率结果。不难看出下一次地震发生的概率在1、2度范围内最高，分别达到了16%和14%。在其他度距离内，概率几乎相等。这表明在目标地震后累计地震矩在1～2度距离范围内会增加

致谢

感谢中国科学院研究生院石耀霖院士、墨西哥大学地球物理系Cinna Lomnitz对本文的指导和建设性意见。

（作者电子信箱，侯燕燕：hyy＠seis.ac.cn）

［1］Flinn E A，Engdahl E R and Hill A R.Seismic and geographical regionalization.Bull.Seis.Soc.Am.，1974，64：771-993

［2］Kagan Y Y and Jackson D D.Seismic gap hypothesis：ten years after.J.Geophys.Res.，1992，96：21419-21 431

［3］Kanamori H.The nature of seismicity patterns before large earthquakes.In：Ewing M，ed.，Earthquake Prediction，1981，Vol.4，Am.Geophys.Union，Washington，DC.，1-19

［4］Lomnitz C.Moment-ratio imaging of seismic regions for earthquake prediction.Geophys.Res.Letters，1993，20：2171-2174

［5］Lomnitz C.Predicting earthquakes with the MRI algorithm.Seismological Research Letters，1996，67（6）：40-46

［6］黄建平，马丽，张晁军.地震矩比成像算法的发展及应用.地震学报，2006，28（5）：529-539

［7］Zhang Chaojun，Shi Yaolin，Huang Jianping，et al.Imaging the earthquake cycle with the Moment-Ratio Method：An exploration.Geofísica Internacional，2009，48（4）：407-414

［8］Lomnitz C.Tectonic feedback and the earthquake cycle.PAGEOPH，1985，123：667-682

Studying global seismicity with cumulative seismic moment

Hou Yanyan and Zhang Chaojun
（China Earthquake Networks Center，Beijing 100045）

Based on the MRI theory by Lomnitz，global earthquakes of M≥7.0 from 1900 to 2003 were analyzed with cumulative seismic moment（CSM）method.The possibility of future earthquake occurrence was estimated through analysis of the change in CSM images before large earthquakes.The result from analyzing the CSM images of 6 earthquakes in different regions showed that the CSM images would change in 5 to 10 years before the earthquakes occurred，and most earthquakes occurred in high-value areas of CSM or second highvalue areas.It was found by actual calculations that better results could be obtained by using differentτvalues in different regions，and the more the number of earthquakes used to calculate，the better results could be obtained.There are generally more than one CSM anomalous areas before some large earthquakes，i.e.，several CSM anomalous areas often appear.This may be related to the seismicities in the study areas.Therefore，the authors thought that the impacts of seismic faults on the energy distribution after an earthquake should also be considered besides considering the seismicities of small earthquakes in different regions in order to obtain reliable CSM images.Statistical results showed that the high probability of next earthquake occurrence would appear in original regions and 2 degree distance in space after the target earthquake occurred.The probability of next earthquake occurrence beyond 3 degree distance only showed little difference.In terms of time，the probability of the next earthquake is the highest within 1 year.This may be related to the aftershock activities.In 5 years，the number of the next earthquakes accounted for more than 70%of all earthquakes.Thus，it should be noticed that seismic energy near the target earthquake would be further released after large earthquakes.

cumulative seismic moment；earthquakes of M≥7.0；next earthquake

P315.0；

A；

10.3969/j.issn.0235-4975.2010.08.011

2010-03-24；

2010-04-06。