因子分析法在脉冲红外热无损检测中的应用

李 政 郭兴旺

(北京航空航天大学 机械工程及自动化学院,北京 100191)

因子分析法在脉冲红外热无损检测中的应用

李 政 郭兴旺

(北京航空航天大学 机械工程及自动化学院,北京 100191)

为了提高脉冲热像法 PT(Pulsed Thermography)的缺陷检测能力,将因子分析法应用于脉冲红外热无损检测的热像序列处理中.介绍了因子分析法的原理,描述了因子分析法处理并重建红外热像序列的步骤.为了考查算法的有效性,对人工内置缺陷的玻璃纤维增强塑料板试件进行了脉冲红外热像检测试验.结果表明:通过因子分析得到的公因子图像可以进行缺陷识别,因子分析法较主分量法处理数据更加灵活;通过公因子重建图像序列后,可增强缺陷信噪比和抑制加热不均效应,从而提高了脉冲热像法的缺陷检测能力.

无损检测;红外热像法;因子分析;热像处理;主分量分析

红外热像无损检测 IR TNDT(Infrared Thermographic Nondestructive examination)具有单次探测面积大、速度快、非接触、可单面检测、安全等特点,在航空航天材料和结构的无损检测中扮演着越来越重要的角色[1].按热激励方式的不同,IR TNDT有脉冲热像法、阶跃热像法、调制热像法等.其中,脉冲热像法由于热激励速度快、检测时间短等优点应用最为广泛,但也有加热不均、噪声大、缺陷探测深度浅等缺点.为了提高脉冲 TNDT的缺陷检测能力,已发展了众多降低噪声干扰、增强缺陷对比度的处理算法[2-3],如脉冲相位法PPT(Pulsed Phase Thermogrophy)[4]、主分量分析PCA(Principal Compenent Analysis)法[5]等 .其中 ,PCA是一种可以将多个指标化为少数指标的一种统计方法,运用在红外热像序列数据分析中,可减小加热不均、噪声等次要信息的干扰,更好地提取所关注的缺陷信息[6].通常,只要变量间存在一定的相关性,前几个主分量往往就具有较高的累积贡献率,从而达到较好的降维目的.然而,在很多情况下只对变量进行降维还不够,还必须对主成分给出符合实际背景和意义的解释,进行这种解释,正是 PCA的困难之处.作为对 PCA的推广和发展,因子分析法[7]可以将变量降维后得到的几个综合指标进行符合实际意义的解释,且可以将各个指标按一定的规则进行变换,从而更好地体现原始变量与综合指标的内在联系.

1 因子分析法原理

一般地,设 x=(x1,x2,…,xn)T是 n维可观测的随机向量,E(x)=μ,D(x)=∑,且设 f=(f1,f2,…,fk)T(k＜n)是不可观测的随机向量,E(f)=0,D(f)=Ik(即 f各分量的方差为 1,而且互不相关).又设随机向量 ε=(ε1,ε2,…,εk)T与f互不相关,且,即各个 ε变量之间互不相关.假定 x满足:

式中,f1,f2,…,fk称为 x的公因子(f1,f2,…,fk对x的每个分量 x1都有影响);ε1,ε2,…,εn称为 x的特殊因子 (εi只对 xi有影响);A=(aij)n×k为因子载荷矩阵,aij表示 fj对 xi的影响程度,称为 xi在 fj的载荷,则称式(1)为正交因子模型.

通过对载荷矩阵的分析,即可知道各个公因子的合理解释.假如一时难以找到合理的解释,可以对公因子及载荷矩阵做进一步的因子旋转,从而找到公因子更合理的解释,这也是因子分析较PCA的一大优点.

因子分析的目的不仅是求出公因子,更主要的是能对每个公因子的实际意义做出解释.当求出的初始因子所代表的意义不是很明确时,不利于对因子进行解释,所以,有必要对因子载荷矩阵进行旋转变换,使得公因子的意义更加明确.若 Γ为任一 k阶正交矩阵,由式(1)得

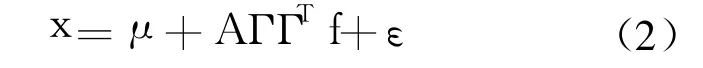
可以证明,对任一正交矩阵 Γ,f*=ΓTf也是满足正交因子模型的公因子向量,而相应的 A*=AΓ是公因子 f*的因子载荷矩阵.利用这一点,在实际应用中常常求出一个载荷矩阵 A后,再按照一定的规则求得合适的正交矩阵 Γ,使得 AΓ能有更好的实际意义,这样一种变换载荷矩阵的方法,称为因子旋转.

因子载荷矩阵的每一列(因子载荷向量)数值越分散,即因子载荷向量的方差越大,越容易对公因子进行合理的解释,所以总希望因子载荷矩阵 A的方差尽可能大.为达到 A的方差最大而进行的因子旋转称为最大方差旋转[7](varimax rotation),也是最常用的因子旋转方法.

2 红外热像序列处理

对红外热像序列进行因子分析处理前,先对原始序列进行预处理,以减少干扰因素及运算量.首先选择时间窗口,只截取降温段的热像序列作为处理对象,然后裁剪掉无关区域,只保留感兴趣区.

预处理后,就可以对热像序列进行因子分析.其中,因子载荷的估计方法有主成分法、主因子法和极大似然法等,公因子的估计方法有加权最小二乘法、回归法等.本文使用主成分法和加权最小二乘法对因子载荷和公因子进行估计,其过程如下:

1)构造数据矩阵.设预处理后的图像序列共有 N帧,每帧大小为 W×H像素,如图 1所示.以每个像素点对应的时间序列作为一个样本,构成数据矩阵的一行,将所有像素点对应的样本依次排成一列,则构造一个 m×n维的数据矩阵 X=,其中,m=W×H,n=N,xi=.矩阵 X示意图如图 2所示.

图1 预处理后的图像序列

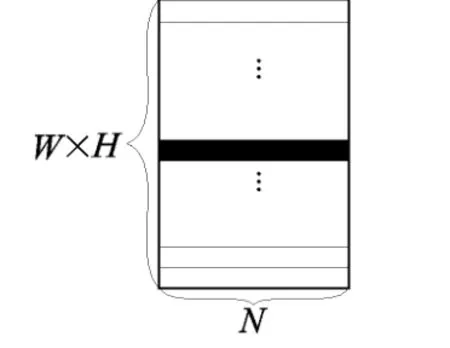
图2 转化后的数据矩阵

2)计算 X的均值向量 μ=(μ1,μ2,…,μn)T及标准差矩阵 V=diag(σ1,σ2,…,σn),然后,利用公式 yi=(xi-μ)/σi(i=1,2,…,m)将矩阵 X标准化,得到标准化矩阵,满足E(y)=0,D(y)=In.

3)求标准化矩阵 Y的协方差矩阵,同时也是矩阵 X的相关矩阵 R,求 R的特征值和标准化特征向量,并确定公因子个数 k.

记 λ1≥λ2≥…≥λn≥0为 R的特征值,其相应的单位正交特征向量为 l1,l2,…,ln.可取 k为满足 (λ1+λ2+… +λk)/(λ1+λ2+… +λn)≥P0的最小正整数(如 P0=0.5或 0.9).一般地,k取为 3或 4即可.

4)构造因子载荷矩阵 A和公因子矩阵 F,并求公因子图像.

记 L=[l1,l2,…,lk],A=diag(λ1,…,λk),令…,k),则因子载荷矩阵为

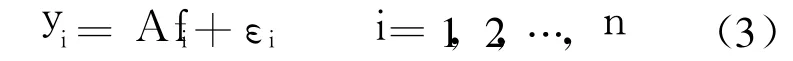
式中,εi为特殊因子.

5)对公因子做出解释,如代表光照不均、热传导、缺陷、表面纹理、噪声等因素.尤其是利用代表内部缺陷因素的公因子图像可以进行缺陷识别.如果不能做出合理的解释,则对其进行适当的因子旋转,使其具有比较合理的意义.

6)利用感兴趣的公因子图像,只适合于缺陷形状识别.为了得到更详细的缺陷特征,从而进行更深入的研究,需要对序列进行重建,恢复图像序列的时序信息.特殊因子 ε中包含的主要是噪声等次要信息,所以,在数据重建时,要去除特殊因子的影响,由式(3)得到重建矩阵 Y的公式:

然后利用均值向量 μ及方差矩阵 V重建数据矩阵 X,写成向量形式为

若只保存式(5)中用到的矩阵和向量,则共需存储的数据为 n×k+k×m+2n=k(m+n)+2n个,远远小于 X的维数 m×n,所以,因子分析法可以有效地对数据进行降维压缩.

最后,将重建的矩阵 X重新排列成 W×H×N的三维矩阵,就重新得到了 N帧 W×H像素的图像序列.数据重建后,还可对其进行更进一步的处理,如DTT(Dynamic Thermal Tomography)[2],PPT等.

3 实验数据处理及结果分析

实验试件是一玻璃纤维增强塑料板试件,板厚 2.5mm,在 1mm深度处预设 φ6mm的人工缺陷.采用单面法检测,用闪光灯加热.

选择从闪光后开始的 100帧图像,裁剪了缺陷附近的 120×82像素点作为处理数据.图 3是预处理后的最佳原始热像(第 13帧,信噪比最高),可以看出,图的左边比右边亮,即存在着加热不均的现象,另外噪声现象也很明显.

图3 最佳原始热像

下面对数据进行因子分析的处理.令公因子的个数为 4,首先不进行因子旋转,图 4是计算出的 4个公因子图像.图 5是 4个公因子对各帧图像的因子载荷曲线,4条曲线分别代表 4个公因子对各帧图像的影响程度.

图4 未经因子旋转的公因子图像

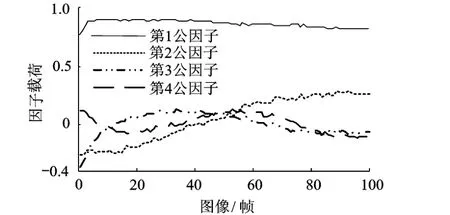
图5 未经因子旋转的因子载荷曲线

图5中的 4条曲线,尤其是第 1,2公因子载荷曲线的方差不大,也没有特别明显的意义,不容易对公因子图像做出合理的解释,所以要进行因子旋转.本文使用方差极大正交旋转法.图 6是因子旋转后的 4个公因子图像.图 7是相应的因子载荷曲线.

图6 方差极大正交旋转公因子图像

图7 方差极大正交旋转因子载荷曲线

在脉冲加热下,由于试件内部缺陷部分和无缺陷部分的导热特性不同,相应区域的表面温度变化会存在差异.一般情况下,分层脱粘缺陷区与无缺陷区的温差曲线是先快速上升再缓慢下降的[8],从图 7中可以看到,第 2公因子的因子载荷曲线也是先快速上升而后缓慢下降的,与温差曲线变化趋势一致,所以,可以认为第 2公因子代表内部缺陷因素.实际上,图 6b与图 3相比,加热不均及噪声对图像造成的负面影响得到了明显的改善,其中间的明亮区域确实很好地显示了内部缺陷.所以,可以使用图 6b来描述此试件的缺陷形状及位置等特征.

另外,其它的公因子可以理解为加热不均、噪声、表面发射率不均等因素.

为了定量地说明因子分析的效果,可以使用图像的信噪比作为图像处理质量的评价指标[2].最佳原始热像及各公因子图像的信噪比如表 1所列.

表 1 图像的信噪比

从表 1中可以看出,因子旋转后的第 2公因子图像(图 6b)的信噪比最高,这也说明了上文针对公因子的解释是正确的,本例中的第 2公因子的确代表了内部缺陷因素.

未经因子旋转的第 2公因子图像的信噪比也比较高,且高于原始热像的信噪比,但不如旋转后的信噪比高.这是因子旋转将其他公因子中的代表缺陷因素的信息更多地转移到了第 2公因子中的缘故.在实际研究中发现,经过因子旋转的公因子图像并不总是比未经旋转的图像质量高,所以说因子旋转只是提供了一种提高图像质量的可能途径.

实际上,PCA法的前 4个主分量图像的像素值是未经因子旋转的公因子图像的3,4)倍,所以它们的显示效果是一样的.所以,因子分析法不但可以得到 PCA法相同的结果,还可以按一定规则进行因子旋转,所以因子分析法较PCA法有更大的灵活性.

为了说明数据重建的作用及其效果,并且验证在重建过程中是否丢失了数据信息,不失一般性,在缺陷区域和无缺陷区域分别选择一点,图 8是两点分别在重建前后的温度曲线及温差曲线.通过对比后发现,重建后的温度曲线减少了毛刺现象,明显比重建前的曲线平滑,而且没有偏离原曲线的波动中心.去噪声的效果在温差曲线中体现得更为明显,温差曲线的高频波动(噪声)明显减小.由此可见,因子分析重建数据不但有效地抑制了噪声干扰,并且也没有丢失原曲线的数据信息.

图8 缺陷点与无缺陷点的温度及温差曲线

4 结 论

1)因子分析通过对公因子进行合理的解释,可以利用代表内部缺陷因素的因子来进行缺陷识别,该公因子图像较原始热像提高了信噪比.

2)与 PCA法相比较,因子分析法可以进行因子旋转,使得变量在降维之后更容易得到解释,说明因子分析法在处理数据方面有较大的灵活性.

3)因子分析法可对数据进行降维和重建,重建的数据有效地抑制了噪声干扰,还保留了与时间和缺陷深度有关的时序信息,进而可以使用其它数据处理方法对缺陷进行表征.

综上所述,作为一种有效的数据降维分解处理算法,因子分析法可以很好地应用于脉冲红外热像无损检测热像序列处理领域,有良好的应用前景.

References)

[1]Ibarra-CastanedoC,Genest M,GuibertS,et al.Inspection of aerospacematerials by pulsed thermography,lock-in thermography and vibrothermography:a comparative study[C]//Knettel K M,Vavilov V P,Miles J J.Proc SPIE Thermosense.Bellingham,WA:SPIE,2007

[2]Vavilov V.Evaluating theefficiency ofdataprocessing algorithms in transient thermal NDT[C]//Burleigh D,Cramer K,Peacock G.Proc SPIE Thermo sense XXVI.Bellingham,WA:SPIE,2004:336-347

[3]Ibarra-Castanedo C,Gonz lez D,Klein M,et al.Infrared image processing and data analysis[J].Infrared Physics＆Technology,2006,46:75-83

[4]郭兴旺,刘颖韬,郭广平,等.脉冲相位法及其在复合材料无损检测中的应用[J].北京航空航天大学学报,2005,31(10):1049-1053 Guo Xingwang,Liu Yingtao,Guo Guangping,et al.Pulsed phase thermography and its application in the NDT of composite materials[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(10):1049-1053(in Chinese)

[5]Marinettia S,Finessob L,Marsilioa E.Matrix factorization methods:application to thermal NDT/E[J].NDT＆E International,2006,39:611-616

[6]郭兴旺,其达拉图.铝试件脉冲红外热无损检测的主分量分析[J].北京航空航天大学学报,2009,35(11):1393-1397 Guo Xingwang,Qidalatu.Principal component analysis used in pulsed thermographic NDT of alum inum specimens[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(11):1393-1397(in Chinese)

[7]余锦华,杨维权.多元统计分析与应用[M].广州:中山大学出版社,2005:210-231 Yu Jinhua,YangWeiquan.Multivariate statistical analysis and application[M].Guangzhou:Sun Yat-sen University Press,2005:210-231(in Chinese)

[8]Guo Xingwang,Qie Fang.Simulating thermal NDT of bonded structuresby FEM[C]//Vavilov V P,Burleigh D D.Proc SPIE Thermosense XXX.Bellingham,WA:SPIE,2008

(编 辑 :张 嵘)

Factor analysis used in pulsed infrared thermographic NDT

Li Zheng Guo Xingwang

(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

To improve the detection capability of pulsed thermography(PT),factor analysis algorithm was applied to image sequence processing in pulsed infrared thermographic nondestructive examination(NDT).The principle of factor analysis was introduced and the procedure of image sequence processing and reconstruction was described.In order to illustrate the validity of this method,a glass fiber reinforced plastic sample with artificial internal defects was tested by PT.It is shown that the common factor images can be used to imp rove the recognition of flaws;factor analysis is more flexible than principal component analysis(PCA);the reconstructed image sequence can improve the defect's signal to noise ratio(SNR)and decrease the nonuniform heating effect,thus the detection capability of PT is enhanced.

nondestructive examination;thermography;factor analysis;thermogram processing;principal compenentanalysis(PCA)

TN 219

A

1001-5965(2010)05-0622-05

2009-06-15

国家自然科学基金资助项目(60672101,50975016);航天支撑技术基金资助项目

李 政(1985-)男,河北承德人,硕士生,lizheng0201@163.com.