基于比例危险-比例优势模型的加速寿命试验设计

黄婷婷 姜同敏

(北京航空航天大学 工程系统工程系,北京 100191)

霍瑞坚

(中国新时代工程咨询有限公司,北京 100034)

基于比例危险-比例优势模型的加速寿命试验设计

黄婷婷 姜同敏

(北京航空航天大学 工程系统工程系,北京 100191)

霍瑞坚

(中国新时代工程咨询有限公司,北京 100034)

将基于信息的优化方法引入基于非参数模型的加速寿命试验优化设计中,针对恒定应力和步进应力两种应力加载方式,分别给出了基于比例危险-比例优势模型的试验优化设计方法.通过对数似然函数建立 Fisher信息矩阵和方差-协方差矩阵,并采用基于信息的优化方法建立最优化问题.这种试验优化设计方法可以有效地提高模型参数评估精度,并且避免了传统的优化方法(即将一个与可靠性相关的函数的渐进方差在一个给定区间内的积分值作为优化目标)当目标函数中给定的积分区间变化时将得到不同优化结果的局限.最后给出了应用该方法进行加速寿命试验优化设计的仿真实例.

试验优化设计;基于信息的优化方法;比例危险-比例优势模型;非参数模型;加速寿命试验

加速寿命试验技术是使用在高应力下较短时间内获得的产品寿命数据外推产品在正常应力下的寿命和可靠性的技术[1].加速模型描述了产品寿命与应力水平之间的关系.加速模型的建立是进行外推的基础,直接影响着外推的精度.加速模型可以分为物理加速模型、经验加速模型和统计加速模型.其中,统计加速模型又可以分为参数模型和非参数模型.参数模型需要预先确定产品的寿命分布形式,然而,如果产品寿命并不服从该寿命分布形式,则可能造成较大的评估误差.非参数模型是一种无分布假设的模型,因此,更加受到研究人员及工程应用人员的青睐.比例危险-比例优势模型[2]通过转移参数将比例危险模型[3]和比例优势模型[4-5]这两种常用的非参数模型结合起来,使这两种模型成为该模型的特殊形式.比例危险-比例优势模型较比例危险模型和比例优势模型具有更广泛的适用范围和评估精度.因此,本文的加速寿命试验优化设计是基于比例危险-比例优势模型进行的.

加速寿命试验优化设计的目的是为了减少运用加速模型进行产品寿命和可靠性外推时的误差,提高评估精度.进行加速寿命试验优化设计通常包括以下几方面的内容:应力水平数及其量值,恒定应力试验时每个应力水平下分配的受试产品个数,或步进应力试验时的应力转换时间等.目前,研究人员运用了多种方法进行加速寿命试验的优化设计.对于非参数模型而言,通常使用的方法是最小化一个与可靠性相关的函数的渐进方差在一个给定区间内的积分值[6-7].然而,这种优化方法的局限性在于,当目标函数中给定的积分区间变化时,可能会得到不同的优化结果.

近几年,基于信息的优化方法已应用于加速寿命试验的优化设计中,该方法可以避免上述优化方法的局限.广泛应用的基于信息的优化方法包括 D-优化方法和 A-优化方法.这两种优化方法的目的都是最大化信息,同时最小化与信息互为倒数的方差.这两种优化方法通过不同的途径得到优化结果,然而,究竟采用哪种优化方法取决于模型参数的特性.

D-优化方法最大化了信息矩阵的行列式值.由于信息矩阵与方差-协方差矩阵互逆,因此,它同时最小化了方差-协方差矩阵的行列式值,也就是最小化了参数评估值联合置信区间的体积[8].该优化方法通常用于模型参数有较强相关性的情况[9].D-优化方法的目标函数是 max det[I].

A-优化方法最小化了信息矩阵逆的迹,即最小化了方差-协方差矩阵的迹,也就是说它最小化了参数评估值方差的和.该优化方法通常用于模型参数相关性较弱的情况[9].A-优化方法的目标函数是 min tr[I-1],即 min tr[∑].

Ng等研究人员将 D-优化方法和 A-优化方法应用于威布尔分布的产品的加速寿命试验优化设计中[9],之后,又将这两种优化方法用于处理极值分布情况的产品样本量分配问题[8].然而,这些基于信息的优化方法目前主要应用于基于参数模型的加速寿命试验优化设计中.本文将这些优化方法应用于基于非参数模型的加速寿命试验优化设计中,分别针对恒定应力和步进应力两种应力加载方式,给出了加速寿命试验优化设计方法.

1 恒定应力加速寿命试验优化设计

1.1 试验过程及优化目标

假设 n个受试产品进行恒定应力加速寿命试验,有 k种应力类型,对于每种应力类型有 q个不同应力水平.那么,加速寿命试验将在 k×q个不同应力组合下进行.定义了分配给应力水平zi1i2…ik=(zi1,zi2,…,zik)T的受试产品个数与参与试验的总产品个数 n的比值,其中,ij=1,2,…,q,j=1,2,…,k.应力组合为 zi1i2…ik的试验在预先确定的 τi1i2…ik时间截尾.图 1给出了当 k=2,q=2时的试验剖面.

图1 多应力类型恒定应力加速寿命试验剖面

优化目标是合理地选取应力水平 zi1i2…ik和每个应力水平下分配的产品比例 pi1i2…ik,ij=1,2,…,q,j=1,2,…,k,使得对模型参数的评估结果更精确,从而减小在正常应力水平下对产品寿命和可靠性评估结果的误差.

1.2 对数似然函数

比例危险-比例优势模型中可靠性函数R(t;z)和概率密度函数 f(t;z)的定义[2]为

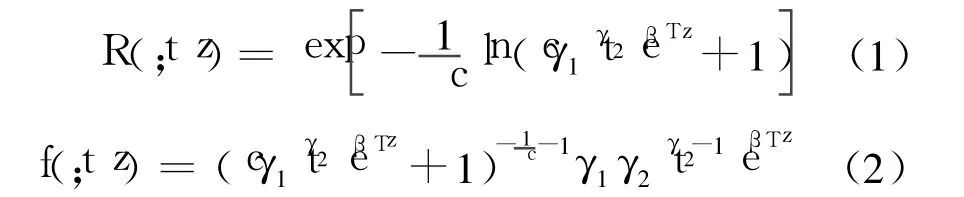
式中,β是模型未知参数向量;z是协变量向量;γ1＞0,γ2＞0是模型未知参数 ;c∈ [0,1]是转移参数.

定义一个指示函数 I:

其中 τ为试验截尾时间.

因此,对于某一个失效数据(t,I,z),对数似然函数可以写为

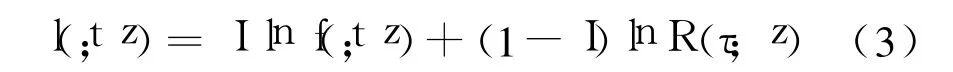
将式(1)和式(2)代入式(3),可以将对数似然函数改写为

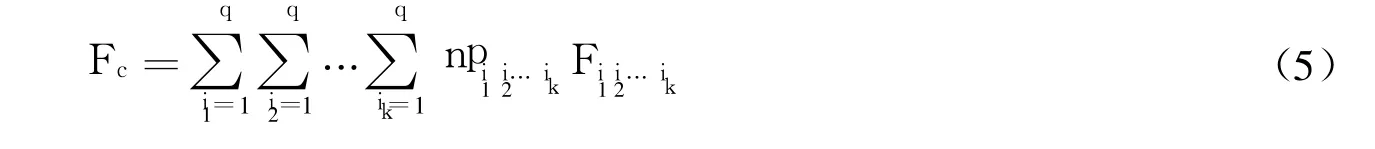
1.3 Fisher信息矩阵及渐进方差-协方差矩阵

计算式(4)给出的对数似然函数对每个模型参数二阶偏导数的负期望值(积分区间为 0到τi1i2…ik),并建立恒定应力条件下的 Fisher信息矩阵 Fc,见式(5).对 Fisher信息矩阵求逆,可以得到方差-协方差矩阵.将加速寿命试验之前通过预试验失效数据或者相似产品历史失效数据得到的模型参数评估值带入方差-协方差矩阵,恒定应力条件下的渐进方差-协方差矩阵,见式(6).

1.4 目标函数和约束条件

在如式(6)的渐进方差-协方差矩阵中代入给定的应力水平和截尾时间,就可以得出给定试验条件下模型参数和的相关度,即协方差.当模型参数相关度远大于 0时,说明模型参数具有较强的相关性,那么,采用 D-优化方法建立最优化问题的目标函数和约束条件.

D-优化方法最大化了信息矩阵的行列式值,这里如式(5)的 Fisher信息矩阵.决策变量是zi1i2…ik和 pi1i2…ik,ij=1,2,…,q,j=1,2,…,k.因此,目标函数及约束条件可以写为

其中,Ni1i2…ik是应力组合 zi1i2…ik下预先确定的所需最小产品失效数.下标 o表示相应应力类型的设计应力水平,下标 u表示相应应力类型的极限应力水平.

当模型参数相关度接近 0时,说明模型参数的相关性较弱,此时,为了减小计算量可采用 A-优化方法建立最优化问题目标函数和约束条件.

A-优化方法最小化了方差-协方差矩阵的迹,这里如式(6)的渐进方差-协方差矩阵.决策变量是 zi1i2…ik和 pi1i2…ik,ij=1,2,…,q,j=1,2,…,k.因此,目标函数及约束条件可以写为

求解最优化问题,可以得到满足约束条件的决策变量最优解,从而给出优化的恒定应力加速寿命试验方案.

2 步进应力加速寿命试验优化设计

2.1 试验过程及优化目标

假设 n个受试产品进行步进应力加速寿命试验,应力水平为 z1和 z2.对于每一个应力水平,有k种不同应力类型,即.该试验在低应力水平 z1下运行到 τ1时间,转换到预先确定的高应力水平 z2运行至预先确定的 τ2时间截尾.步进应力加速寿命试验剖面如图 2所示.

图2 多应力类型步进应力加速寿命试验剖面

优化目标是合理地选取 z1和 τ1,使得对模型参数的评估结果最精确,从而减小在正常应力水平下对产品寿命和可靠性评估结果的误差.

2.2 对数似然函数

采用累积损伤模型建立步进应力加速寿命试验中的对数似然函数.累积损伤模型假设产品剩余寿命只与其损伤量有关,而与损伤量累积方式无关[10].

考虑试验在低应力水平 z1下运行到 τ1时间,然后在高应力水平 z2下运行到 τ2时间截尾.对于应力水平 z2来说,它有一个等效的起始时间 s.即受试产品在应力水平 z1下运行 τ1时间的损伤量相当于受试产品在应力水平 z2下运行 s时间的损伤量.依据累积损伤模型,s可以由下式计算:

即

因此,受试产品的累积分布函数可以表达为

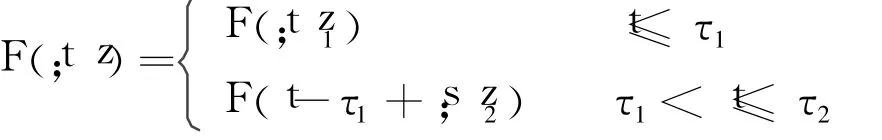
相应地,受试产品的概率密度函数为

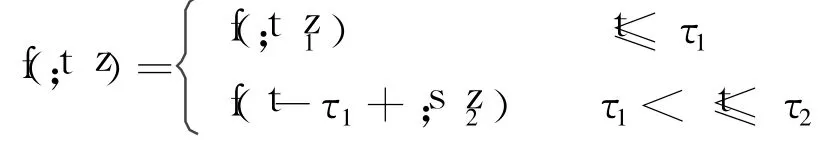
定义 2个指示函数 I1和 I2:

其中,τ1≤τ2.

因此,对于某一个失效数据(t,I1,I2,z),对数似然函数可以表达为

将式(1)和式(2)代入式(9),可以将对数似然函数改写为

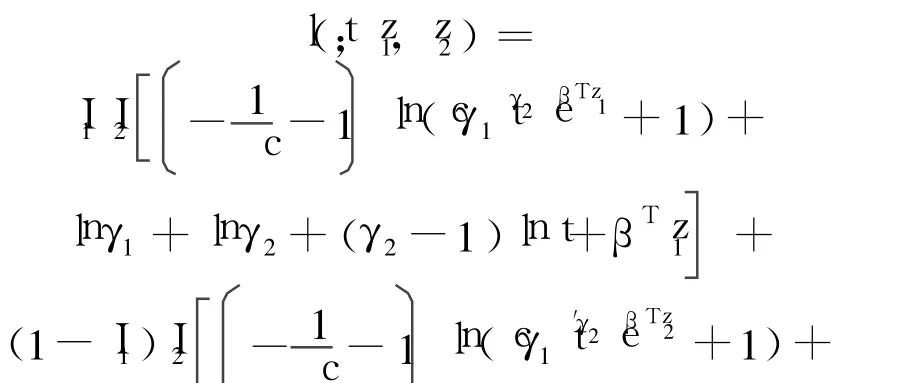
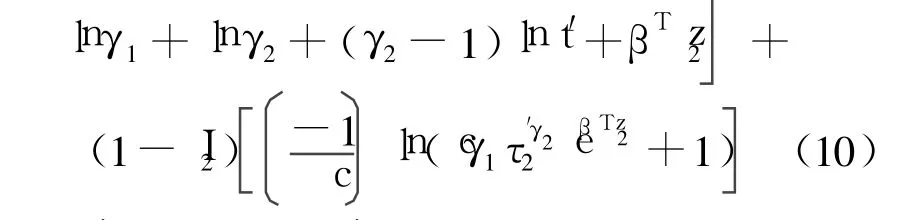
2.3 Fisher信息矩阵及渐进方差-协方差矩阵

计算式(10)给出的对数似然函数对每个模型参数二阶偏导数的负期望值(积分区间为 0到τ2),并建立步进应力条件下的 Fisher信息矩阵Fs见式 (11).

对 Fisher信息矩阵求逆,可以得到方差-协方差矩阵,带入模型参数评估值,步进应力条件下的渐进方差-协方差矩阵见式(12).

2.4 目标函数和约束条件

在如式(12)的渐进方差-协方差矩阵中代入给定的应力水平和截尾时间,就可以得出给定试验条件下模型参数和的相关度,即协方差.当模型参数相关度远大于 0时,说明模型参数具有较强的相关性,那么,采用 D-优化方法建立最优化问题的目标函数和约束条件.

D-优化方法最大化了信息矩阵的行列式值,这里如式(11)的 Fisher信息矩阵.决策变量是 z1和 τ1.因此,目标函数及约束条件可以写为

其中,N1是应力水平 z1下预先确定的所需最小产品失效数.

当模型参数相关度接近 0时,说明模型参数的相关性较弱,此时,为了减小计算量可以采用A-优化方法建立最优化问题目标函数和约束条件.

A-优化方法最小化了方差-协方差矩阵的迹,这里如式(12)的渐进方差-协方差矩阵.决策变量是 z1和 τ1.因此,目标函数及约束条件可以写为

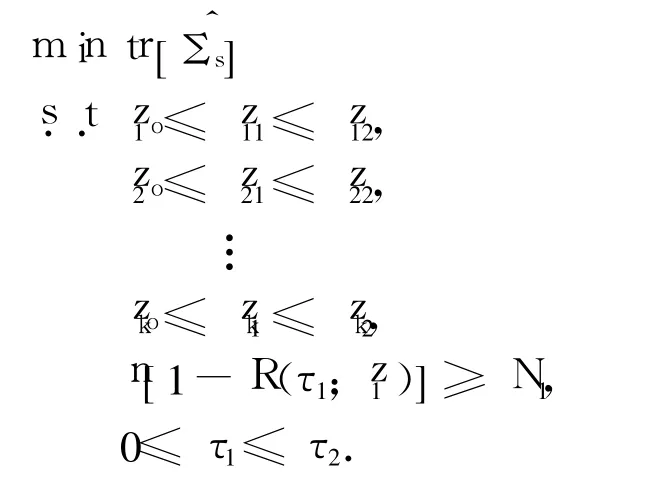
求解最优化问题,可以得到满足约束条件的决策变量最优解,从而给出优化的步进应力加速寿命试验方案.

3 仿真实例

3.1 恒定应力加速寿命试验优化设计实例

假设某产品进行三水平恒定应力加速寿命试验,试验应力为温度应力.可获得的受试产品数量为 300个.受试产品的工作极限为 200℃.对于每个应力水平,截尾时间为 300 h,并且要求每个应力水平下至少有 20个受试产品失效.

温度应力水平值依照阿伦尼斯模型转换为100K-1.因此,正常应力水平 25℃以及产品工作极限应力水平 200℃分别转换为 0.336和 0.211.假设采用比例危险-比例优势模型对该产品加速寿命试验预试验的失效数据进行评估得到的模型参数评估值为:β=-60,c=0.5,γ1=2,γ2=3.那么,针对正常应力水平下 300个受试产品运行300h的情况,计算得到模型参数的相关度为6.40.因此,认为模型参数相关性不可以忽略,采用 D-优化方法进行试验优化设计.目标函数是如式(5)的 Fisher信息矩阵的行列式值,决策变量是 zi和 pi,i=1,2,3.对于该问题,建立目标函数和约束条件如下:

其中,n=300;τ=300;Ni=20,i=1,2,3.

满足约束条件的决策变量最优解为 z1=0.277,z2=0.255,z3=0.215,p1=0.454,p2=0.308,p3=0.238.因此,该产品恒定应力加速寿命试验最优试验方案如表 1所示.

表 1 恒定应力加速寿命试验最优试验方案

目标函数值为 3258595.14.由于信息矩阵与方差-协方差矩阵互逆,因此,方差-协方差矩阵的行列式值即模型参数评估值联合置信区间的体积为 3.069×10-7.可以看出,通过基于信息的优化方法对恒定应力加速寿命试验进行优化设计可以有效地提高模型参数的评估精度.

3.2 步进应力加速寿命试验优化设计实例

假设一产品进行两水平步进应力加速寿命试验,试验应力为温度应力.可获得的受试产品数量为 300个.受试产品的工作极限为 200℃.试验在低应力水平 z1进行 τ1时间后,转到高应力水平 z2(取为产品工作极限 200℃),并在 τ2=300h截尾.要求低应力水平 z1下至少有 50个受试产品失效.

假设模型参数评估值与恒定应力加速寿命试验优化设计实例中相同,那么,模型参数相关性不可以忽略,采用 D-优化方法进行试验优化设计.目标函数是如式(11)的 Fisher信息矩阵的行列式值,决策变量是 z1和 τ1.对于该问题,建立目标函数和约束条件如下:

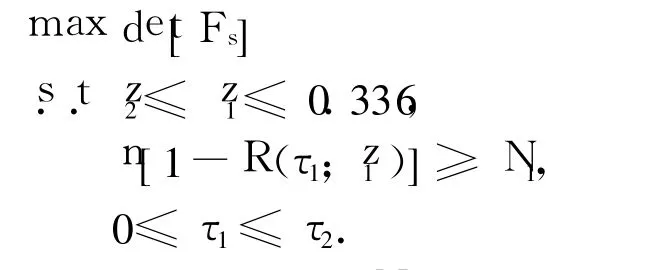
其中,z2=0.211;n=300;N1=50;τ2=300.

满足约束条件的决策变量最优解为 z1=0.258,τ1=156.8.因此,该产品步进应力加速寿命试验最优试验方案如表 2所示.

表 2 步进应力加速寿命试验最优试验方案

目标函数值为 10546 881.35.由于信息矩阵与方差-协方差矩阵互逆,因此,方差-协方差矩阵的行列式值即模型参数评估值联合置信区间的体积为 9.481×10-8.可以看出,通过基于信息的优化方法对步进应力加速寿命试验进行优化设计可以有效地提高模型参数的评估精度.

4 结束语

本文基于比例危险-比例优势模型,分别针对恒定应力和步进应力两种应力加载方式给出了加速寿命试验优化设计方法.通过对数似然函数建立了 Fisher信息矩阵和方差-协方差矩阵,并采用基于信息的优化方法建立了最优化问题.本方法以信息矩阵的行列式值或方差-协方差矩阵的迹为优化目标,从而避免了传统的基于非参数模型的加速寿命试验优化设计方法中由于目标函数中积分区间变化而造成的优化结果不一致的问题.最后给出了运用该方法进行加速寿命试验优化设计的仿真实例.仿真实例结果表明这种试验优化设计方法可以有效地提高模型参数的评估精度.

References)

[1]Elsayed E A.Reliability engineering[M].Massachusetts:Addison-Wesley,1996:107-173

[2]Huang T.Elsayed E A,Jiang T.An ALT proportional hazard-proportional oddsmodel[C]//Proc of the 14th ISSAT International Conference on Reliability and Quality in Design.Florida:[s.n.],2008:39-43

[3]Cox D R.Regression models and life-tables[J].Journal of the Royal Statistical Society,Series B(Methodological),1972,34(2):187-220

[4]Brass W.Mortality models and their uses in demography[J].Transactions of the Faculty of Actuaries,1974,33:122-133

[5]ZhangH.Modeling and planning accelerated life testing with proportional odds[D].New Jersey:Department of Industrial and Systems Engineering,Rutgers University,2007

[6]Elsayed E A,Jiao L.Optimal design of proportional hazards based accelerated life testing plans[J].International Journal of Materials＆Product Technology,2002,17:411-424

[7]Elsayed E A,Zhang H.Design of optimum multiple-stress accelerated life testing plans based on proportional oddsmodel[J].International Journal of Product Development,2009,7(3/4):186-198

[8]NgH K T,Chan PS,Balakrishnan N.Optimal progressive censoring plans for theWeibull distribution[J].American Statistical Association and the American Society for Quality Technometrics,2004,46(4):470-481

[9]Ng H K T,Balakrishnan N,Chan P S.Optimal sample size allocation for tests with multiple levels of stress with extreme value regression[J].Naval Research Logistics,2007,54:237-249

[10]Nelson W.Accelerated life testing step-stress models and data analysis[J].IEEE Transon Reliability,1980,29:103-108

(编 辑 :娄 嘉)

Optimum design of accelerated life testing based on proportional hazards-proportional oddsmodel

Huang Tingting Jiang Tongmin

(Dept.of System Engineering of Engineering Technology,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Huo Ruijian

(China XinshidaiCompany,Beijing 100034,China)

Information based optimality criteria were adopted in the optimum design of accelerated life testing(ALT)based on non-para metric model.The optimum design of accelerated life testing based on proportional hazards-proportional odds model was processed for constant stress loading and step stress loading respectively.The optimum problem was established by defining Fisher information matrix and variance-covariance matrix based on log-likelihood function.These optimality criteria could improve the accuracy of model parameter estimates effectively and they avoided the drawbacks of the traditional optimality criteria which minimized the integral of asymptotic variance of a reliability-related function over a specified time period undernormal operating condition that might result in different optimum solutions with the varying of the length of the time period.Numerical examples were given to demonstrate these methods.

test planning;information based optimality criteria;proportional hazards-proportional odds model;non-parametricmodel;accelerated life testing

TB 114.3

A

1001-5965(2010)05-0570-06

2009-10-14

黄婷婷(1981-),女,新疆乌鲁木齐人,博士生,huangtingting@dse.buaa.edu.cn.