不确定机组组合处理方法评述

赵晋泉，汪 晶

（河海大学能源与电气学院，江苏南京210098）

在电力系统的短期经济运行中，机组组合是一个核心问题。它是在一个调度周期内，通过合理安排火电机组的开、停以及出力大小，在满足系统运行约束和机组自身约束的前提下，实现全系统总运行成本最低的目标。半个多世纪以来，随着技术进步、网络安全性、环境保护和节约能源要求提高、电力市场化改革以及多种可再生能源发电的接入，机组组合问题不断发展，始终吸引着电力工业界和学者的目光。电力系统机组组合问题本质上是一个不确定性优化问题。传统机组组合问题[1，2]把这种不确定性隐式表达为一个备用不等式约束。这样处理存在两种可能。一是过高估计了风险，造成成本太高，不经济；二是低估了风险，造成系统运行不安全。因此，更加合理地考虑机组组合问题中的随机性，在安全和经济之间寻找更好的折衷点一直是研究的重点。随着风力发电大量接入电网，由于风能随机性强，机组组合问题中的随机性更受到重视，同时数学上随机优化技术的发展也为随机机组组合的应用带来了可能。文中对基于方案树的随机规划、模糊优化和机会约束规划3种显式处理不确定性的技术进行了分析、比较和评述。

1传统机组组合问题

不计备用机组组合问题的数学模型为：

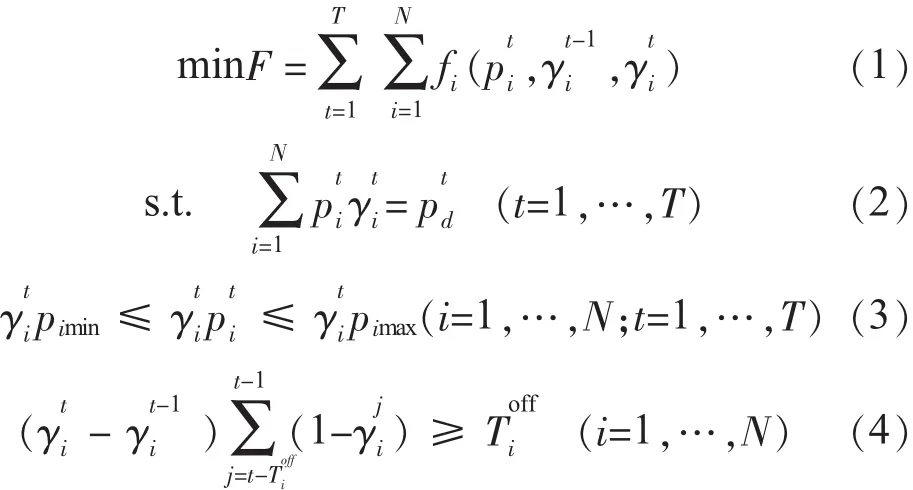
式中：T为总时段数；N为机组总数；F为总发电成本；γti为机组i在t时段的状态；pti为机组i在 t时段的出力；ptd为预测的第t时段系统总负荷；式（3）为机组出力约束，pimax，pimin分别为i机组的最大和最小出力限值；式（4）、式（5）为机组最小启停时间约束；Toin，Toiff分别为i机组的最小运行和最小停机时间。

不计备用的机组组合问题仅是系统负荷的函数，其解可表示为：

式中：P为pt的向量形式。如果次日系统实际负荷

dd完全与预测相同，则上述不计备用的机组组合问题可得到满足经济和安全的最优解。

然而实际电力系统运行存在很多不确定性。大致包括两类不确定性事件：负荷预测偏差和设备的不可靠。一般而言，可以把机组组合问题中的不确定性隐式表达为一个固定备用需求的不等式约束，加入上述模型中，如下式：

式中：Rt为t时段系统备用需求，通常取为一定比例的系统负荷（如10%）或系统中最大的发电机额定功率。

式中：R为Rt的向量形式。计及备用的机组组合问题构成了机组组合的确定性模型。它简单，求解方便，但也存在两种可能，Rt太大，造成不经济；或者Rt太小，造成不安全。因此，需要寻求能够更加合理地处理机组组合问题中随机性的方法。数学上不确定优化技术的发展为电力系统随机机组组合的提出和应用奠定了基础。考虑不确定事件概率，显式表达不确定性成为近期的研究热点。

2不确定性机组组合问题

负荷预测偏差属于连续事件，而诸如发电机和线路故障退出等设备不可靠属于离散事件。随着风力发电大量接入电网，由于风能随机性强，则机组组合问题中的风电出力也是一个不确定量。一般而言，风电场根据风力的大小来决定其发电量，不受调度员的控制。因此，风电出力相当于传统机组组合问题中的一个负的负荷，则风电的随机性也可处理为负荷的随机性。

在不确定性规划中，对不确定问题的处理有2种方法[3]：一是随机规划，二是模糊规划。基于这两类数学方法的原理，比较了3种显式处理机组组合问题中不确定性的方法：基于方案树的随机规划法[4]，模糊优化方法和基于机会约束规划的方法。

2.1基于方案树的随机规划机组组合问题

1996年法国学者Carpentier等人[5]和美国学者Takriti等人[6]分别提出了基于方案树的随机规划机组组合模型。该方法将无限维的不确定性用有限数量的场景（或称方案、情形）来模拟，并编组为一个方案树，并给定各方案相应的概率作为权重，求取各方案综合的最优发电计划。在该方法中，目标函数变为各种方案的加权发电成本最小。

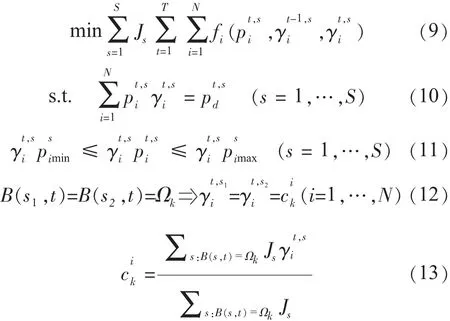
式中：S为方案树中的总方案数；Js为方案s的概率，满足：

负荷平衡约束条件（10）考虑了多种可能的负荷情况；约束条件（12）为联系各种不同方案的束约束（Bundle-constraints），B（s1，t）代表在方案 s1下从开始到t时段的部分决策；式（12）表示如果根据t时段的信息无法区分出在时段t内2种不同的情况s1和s2，那么这2种方案从开始到t时段时的决策一样。束约束属于系统耦合约束。方案树如图1所示。

图1方案树

基于方案树的机组组合问题是各种方案发生概率和具体方案的函数，表示为如下形式：

式中：JS，分别为 JS，的向量形式。

式（14）存在2个特例。一是：

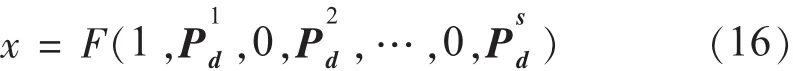
式（16）表示在机组组合问题中不发生任何随机事件，则此时该问题退化为不考虑备用的机组组合问题，见式（6）。

在该方法中，方案树的选择和确定至关重要，方案选择过多，计算复杂度和计算时间成倍增长；方案选择过少，则无法模拟各种可能从而存在一定的风险。

在式（9—13）的基础上，若增加考虑网络安全约束，从而可考虑网络中支路故障的随机性，形成计及网络安全约束的随机机组组合问题[7，8]。

仅通过方案分解这种随机规划方法考虑不确定性，仍可能存在一些风险。如负荷变化这种连续变化事件用方案树来离散处理，可能无法准确描述该类事件的可能情况，即方案树上的有限种方案终究是不能涵盖机组组合问题中所有可能存在的不确定性。文献[9]提出双重随机性考虑：即固定备用大小的传统做法与方案树随机优化方法相结合。用固定备用来考虑系统中负荷预测偏差这类连续事件的随机性，而用随机优化处理发电机和线路故障跳出这类大的随机离散事件。因此需要在备用的容量和选取的方案间找到一个平衡点，使得该问题既可靠又安全。

2.2模糊机组组合问题

模糊优化理论起源于20世纪70年代Bellman和Zadeh提出的模糊决策概念和模糊环境下的决策模型[10]。将优化问题中不确定量用模糊方式表达，不仅能表示可行解，而且对不可行解可按距离可行域的远近程度进行模糊处理，是处理不确定性信息的有效方法。

由于系统负荷的随机性，可处理成模糊量，从而机组组合的总成本也同样是模糊数，经过模糊处理的系统负荷可表示为某一个区间的值而不是一个具体的可能存在误差的值。假设采用三角模糊函数表示负荷隶属度函数：

其隶属度函数如图2所示。

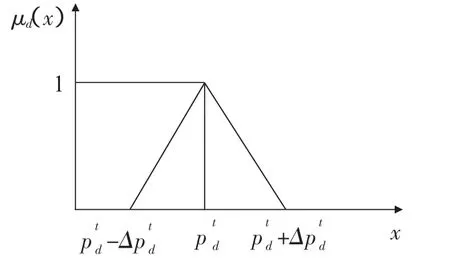
图2负荷的隶属度函数

设采用梯形函数表示总成本的隶属度函数：

式中：F0为系统的理想成本；F0+ΔF为最大可接受成本。隶属度函数如图3所示。

这样，原来成本最小的目标函数相应变为最大程度的满足各种模糊关系。目标函数如下：

max μ （19）

s.t. μ ≤ μd（x） （20）

μ ≤ μF（x） （21）

0≤ μ ≤1 （22）

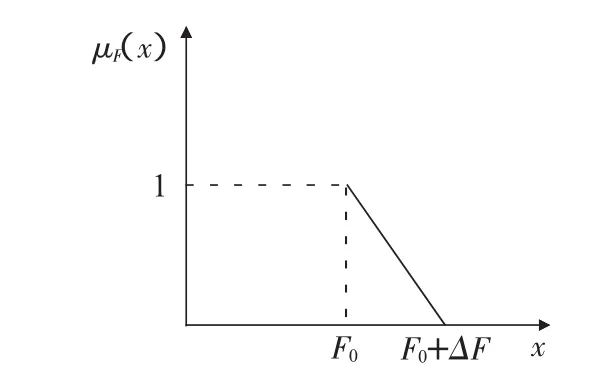
图3总成本的隶属度函数

在模糊集理论中，式(19—22)可等价于下面的目标函数:

上述分段线性隶属度函数，对于约束条件的满足关系描述得比较直观。但文献[11]首次将模糊集理论用于处理不确定性机组组合问题时，采用的是连续的隶属度函数。2种表示方法都能起到很好的模糊处理的效果。在以后的研究过程中，连续[12]与分段线性[13，14]的模糊函数都得到了很好的应用。

模糊机组组合问题[15-18]是系统负荷向量Pd和负荷预测最大允许偏差向量ΔPd的函数，其解可近似表示为如下形式：x=F（ΔPd，Pd） （24）当所有Δ=0时，其存在特解：x*= （0，Pd） （25）

此时，特解的形式与式（6）等价，则该问题退化为不计备用的机组组合问题。

该方法中，使用隶属度函数来描述差异的中间过渡，处理了模糊现象，因此，隶属度函数的选择对问题的求解影响较大。

模糊逻辑是另一种利用模糊优化理论处理不确定性问题的方法。它主要对工程中很难用精确数学关系表示的问题采用模糊逻辑规则的推理形式描述，文献[19，20]将这种模糊逻辑方法应用于机组组合中。其方法如下：对该问题中的模糊输入量选取适当的隶属度函数，使之有对应的模糊语义然后根据输入的模糊语义通过模糊规则推出输出的模糊语义，最后通过逆模糊化得到输出的准确值。但是，该方法的模糊推理规则是与具体研究对象相关的，因人因景而异，它对优化结果有直接影响。

2.3基于机会约束规划的机组组合问题

机会约束规划是随机规划的重要分支，由Char-nes和Cooper首先提出，主要针对的是约束条件中含有随机变量，且必须在观测到随机变量的实现之前做出决策的问题[21]。机会约束规划方法是将不确定性问题中的软约束 （即允许一定程度不满足的约束）以一定的概率进行松弛处理，用约束条件成立的概率来表示和量度风险[22]，达到通过冒一定风险节省成本的目的，也是一种较好的不确定性风险管理方法。

针对固定备用约束（见式（7）），可采用通过冒风险的方式使之以一定置信度满足。这样由于约束条件的松弛，可以节省一部分发电成本。因此，该方法就是通过对利润和风险之间的协调，找到一个折衷点。其数学模型大致为：

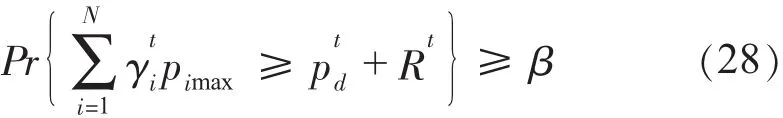
式中，Pr｛｝为 ｛｝中事件成立的概率；α、β分别为决策者预先给定的对应目标函数和约束条件的置信水平；F¯为机组组合目标函数F在概率水平至少是α时所取的最小值。

该模型要求系统调度员在（0，1）范围内适当地选择约束条件的置信水平和相应的调度方案，并允许所形成的调度方案在某些比较极端的情况下不满足约束条件，但这些情况发生的概率必须小于该置信水平。该置信水平的高低可以反映出对电力系统运行水平的要求。

基于机会约束规划的机组组合问题是目标函数和备用约束条件置信水平α，β的函数，同时也是系统负荷和系统备用的函数。其解可用如下形式表示为：

x=F （α，β，R，Pd） （29）

置信水平β的值是备用约束不等式成立的概率。当α=β=1.0时，则此时备用约束条件完全成立，特解形式如下：

x=F （R，Pd） （30）此时式(28)变为式(7)，该问题退化为计及固定备用约束的机组组合问题。

当α=β=0时，此时完全没有考虑系统备用，此时的特解表示为：

x=F （Pd） （31）

此时模型退化为不考虑备用的机组组合问题（6）。

文献[23]首次将机会约束规划用来处理机组组合问题的不确定性，松弛处理的是负荷平衡约束，没有考虑备用约束。其数学模型为：

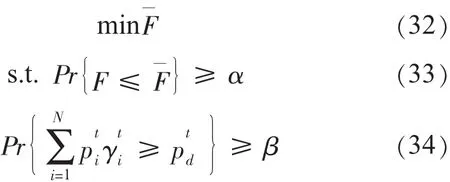
这种处理使负荷平衡约束的置信水平必须取得很大，否则风险比较大。与这种方法相比，在必须满足负荷平衡约束的基础上松弛备用约束，如果置信水平取得合适，则相对安全。

3 3种不确定性处理方法的比较

上述3种方法在处理机组组合中的不确定性时都能较好的考虑电力系统运行过程中出现的不确定情况，并且与传统的机组组合相比都能获得一定的经济效益。

基于方案树的随机规划处理方法对系统中不确定方案的形式没有要求，无论是离散事件还是连续事件，它都能通过方案树描述，并且该处理对机组组合问题的求解方法没有太多要求，用传统的分解方法即可。但该技术通过将连续事件离散化处理，系统难免会有风险存在，并且计算量很大，无论是方案的选择，还是后面的分解计算，都有一定的复杂性。并且方案树的选择也至关重要，它既关系到计算复杂度又关系到解的质量。

模糊优化根据隶属度函数对系统中模糊量直接进行松弛，因此隶属度参数的选取，会对系统的优化结果产生影响。也就是说该方法对隶属度参数有较大的依赖性。目前，这些隶属度函数参数的选取常常根据系统运行的条件，结合调度运行人员的经验来确定，没有严格的理论依据。该方法能很好的对连续变化量进行模糊处理，且计算比较简单，但对机组组合问题中的离散随机事件处理不好。

基于机会约束规划的机组组合方法中，约束条件和目标成本的实现概率为方案的风险，这种方案风险的直观定义方式，可以帮助决策者协调利润和风险，但调度方案也大大依赖于置信水平。由于优化模型中引入了随机变量和机会约束，如果运用常规算法则需要将随机规划模型转化为确定性优化模型，实际应用中往往难以转化。而求解该模型需要用到随机模拟技术和现代智能算法。对求解方法要求较高，求解相对复杂。

表1为不同角度3种方法的定性比较结果。

4结束语

电力系统机组组合问题是典型的不确定性优化问题，随着以风力发电等可再生能源大量接入电网，该问题的随机性更强了。文中对基于方案树的随机规划法、模糊优化方法和基于机会约束规划的方法等3种技术进行了分析和比较。本文认为：

（1）在处理考虑负荷的随机性和涉及风电波动性的机组组合问题时，模糊优化方法简单直观，计算量也相对较小，是一种比较好的处理技术。

表1 3种处理机组组合不确定性的方法比较

（2）在需要处理如发电机、线路退出等随机事件时，可通过选择合适的方案树来模拟，其发生概率也能提供。因此，基于方案树的随机规划方法有较大的优势。

（3）在某些不具备直接给出事件概率和模糊参数的情形下，调度人员可以根据系统的实际情况给出一个置信水平，兼顾费用和风险，通过机会约束规划方法，实现最优化决策。

因此，在解决不确定机组组合问题时，可根据实际情况来选择不同的技术。

[1]陈浩勇，王锡凡.机组组合问题的优化方法综述[J].电力系统自动化，1999，23（4）：51-56．

[2]NARAYANA P P.Unit Commitment-a Bibliographical Survey[J]．IEEE Transactions on Power Systems，2004，19（2）：1196-1205．

[3]刘宝碇，赵瑞清.随机规划与模糊规划[M].北京：清华大学出版社，1998.

[4]SHIINA T，BIRGE J R.Stochastic Unit Commitment Problem[J].International Transactions in Operational Research，2004， 11：19-32.

[5]CARPENTIER P，COHEN G，CULIOLI J C，et al.Stochastic Optim ization of Unit Comm itment:a New Decomposition Framework[J].IEEE Transactions on Power Systems， 1996，11（2）： 1067-1073.

[6]TAKRITI S，BIRGE J， LONG E.A Stochastic Model for the Unit Comm itment Problem[J].IEEE Transactions on Power Systems， 1996， 11（3）： 1497-1508.

[7]WUL，SHAHIDEHPOURM，LIT.StochasticSecurity-constrained Unit Comm itment[J].IEEE Transactions on Power Systems，2007， 22（2）： 800-811.

[8]BOUFFARD F，GALIANA F D.Stochastic Security for Operations Planning with Significant Wind Power Generation[J].IEEE Transactions on Power Systems，2008，23（2）：306-316.

[9]RUIZ P A，PHILBRICK C R，ZAK E，et al.Uncertainty Management in the Unit Commitment problem[J].IEEE Transactions on Power Systems， 2009， 24（2）：642-651.

[10]唐加福，汪定伟．模糊优化理论与方法的研究综述[J]．控制理论与应用，2000，17（2）：159-164．

[11]SU C C，HUS Y Y.Fuzzy Dynamic Programming:an Application to Unit Commitment[J].IEEE Transactions on Power Systems， 1991， 6（3）：1231-1237.

[12]LIANG R H，LIAO J H.A Fuzzy-Optimization Approach for Generation Scheduling w ith Wind and Solar Energy Systems[J].IEEE Transactionson Power Systems，2007，22（4）：1665-1674.

[13]EL-SAADAWI M M，TANTAWI M A，TAWFIK.A Fuzzy Optimization-Based Approach to Large Scale Thermal Unit Comm itment[J].Electric Power Systems Research， 2004，72：245-252.

[14]ATTAVIRIYANUPAP P，KITA H，TANAKA E，et al.A Fuzzy-Optim ization Approach to Dynamic Economic Dispatch Considering Uncertainties[J].IEEE Transactions on Power Systems，2004， 19（3）：1299-1307.

[15]艾 琳，华 栋．基于模糊优化和内点法的水火电系统短期经济调度[J]．电力自动化设备，2008，28（8）：46-50．

[16]VLADIM IRO M，PUN S H.Economic Dispatch Model with Fuzzy Wind Constraints and Attitudes of Dispatchers[J].IEEE Transactions on Power Systems，2005，20 （4） ：2143-2145．

[17]VENKATESH B，PENG Y，GOOI H B，et al.Fuzzy M ILP Unit Comm itment Incorporating Wind Generators[J].IEEE Transactions on Power Systems， 2008， 19（3）： 1738-1746.

[18]TUOHY A，MEIBOM P，DENNY E，et al.Unit Comm itment for Systems with Significant Wind Penetration[J].IEEE Transactions on Power Systems， 2009， 24（2）：592-601.

[19]SEYADRASOUL S，PRASAD N R，SMOLLECK H A.A Fuzzy Logic Approach to Unit Comm itment[J].IEEE Transactions on Power Systems， 1997， 12（2）：988-995.

[20]MANTAWY A H.A Genetic A lgorithm Solution to a New FuzzyUnit Comm itment Model[J].Electric Power Systems Research， 2004， 72：171-178.

[21]孙元章，吴 俊，李国杰，等.基于风速预测和随机规划的含风电场电力系统动态经济调度[J].中国电机工程学报，2009，29（4）：41-47.

[22]朱建全，吴杰康．水火电力系统短期优化调度的不确定性模型[J]．电力系统自动化，2008，32（6）：51-54.

[23]OZTURK U A，MAZUMDAR M.A Solution to the Stochastic Unit Commitment Problem Using Chance Constrained Programm ing[J].IEEE Transactions on Power Systems，2004， 19（3）：1589-1598.