月牙泉水位变化的原因分析

尹念文,侯燕军,李 彬

(甘肃省地质环境监测院,甘肃 兰州 730050)

1 月牙泉水位动态特征

从历史文字记载中可以看出,月牙泉在东汉时期就已成为名胜,在《重修肃州新志》、《沙州卫志月牙泉条》记载“(月牙泉)其水澄澈,环以流沙,虽遇烈风,而泉不为沙掩,盖名亦也……”。说明了月牙泉在其形成后的历史过程中,泉水的动态一直是比较稳定的,至今还没有发现有关月牙泉水位下降和干涸的历史记录,所见文字多是数千年不干涸,沙掩不没等词语,说明月牙泉存在的历史悠久,在早期历史时期泉水的动态一直比较稳定。

自 20世纪 60年代以来,月牙泉水位多年动态呈现出单边向下,持续走低的变化趋势,到 1998年为止,月牙泉水位总降幅达 10.0m左右,与区域地下水的降幅基本一致(图 1)。

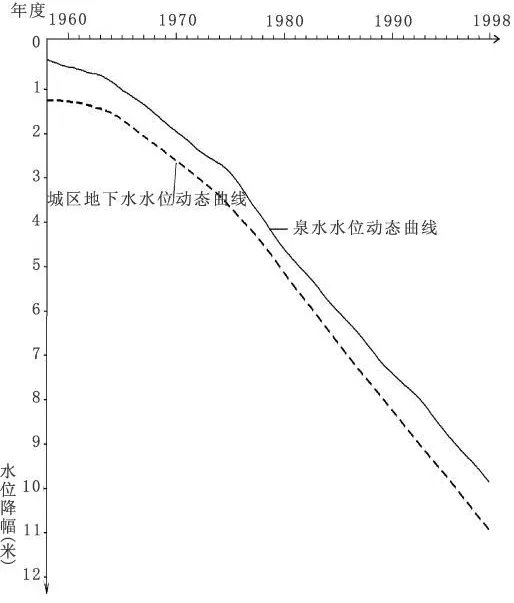
图1 月牙泉水位与区域地下水位动态曲线对比图

从 1997年到 2007年的十年里,月牙泉湖水位继续下降,泉底出露。2008年 6月中旬实测月牙泉水位由 1132.81m上升到 1134.68m,上升高度约 1.80m。月牙泉水位发生这种变化的原因,可以从泉域地下水的补、径、排条件进行分析。

2 月牙泉域地下水的补给、径流及排泄条件

2.1 泉域地下水的补给条件

根据地下水流场图分析(图 2),月牙泉域地下水的补给来源为西部党河河床渗漏和总干渠、东干渠、沙山支渠渗漏及田间灌溉水入渗补给等。泉域地下水与区域地下水是一个含水体系,两者之间有着密切的水力联系。根据区域地下水、泉域地下水的流场特征和水化学特征分析,西北部(包括西南部)地下潜水的侧向流入是月牙泉泉水的主要补给来源[1]。由于区内降水量极少,蒸发强烈,加之范围小,地下水埋藏一般较深,故降水对泉域地下水基本上没有多大补给作用。

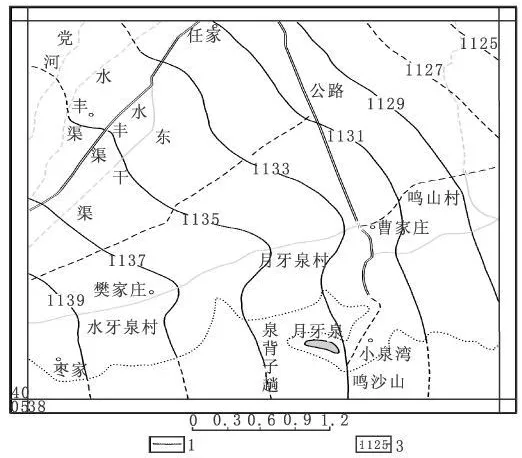
图2 月牙泉及周围地区地下水动力场分布图(1998)

2.2 泉域地下水的径流、排泄条件

泉域地下水的径流途径是由西向东或东北方向,最终的排泄处是伊塘湖[2],由于含水层颗粒较细,因此,径流速度比较缓慢;而泉水的排泄方式包括侧向流出,人工开采,水面蒸发,潜水蒸发和植物蒸腾五个方面,其中人工开采、水面蒸发和侧向流出是泉水的主要排泄方式。

综上,从月牙泉的补给条件来看,该泉是以西北部党河冲洪积平原地下水为主要补给来源,在地形较低洼处出露形成的泉水,但泉水的动态严格受北部平原地区地下水位变化的影响[1],北部平原区地下水位的升降必然导致月牙泉水位发生相应的变化,两者在动态方面具有连动作用。月牙泉水位的变化主要是由区域地下水位变化引起的,从图 1也可以看出,泉水与区域地下水的水位动态是一致的。

2.3 泉域地下水均衡式

泉域地下水均衡方程式可用下式表示：

ΔQ=(Q河+Q渠+Q田+Q降凝+Q雨洪+Q潜+Q侧入+Q回归)-(Q蒸发+Q泉+Q开+Q侧出) (1)

式中：Q河为河道水入渗补给量(万 m3/a);Q渠为渠系水入渗补给量(万m3/a);Q田为田间灌溉水入渗补给量(万 m3/a);Q降凝为降水、凝结水入渗补给量(万 m3/a);Q雨洪为雨洪散流入渗补给量(万 m3/a);Q潜为沟谷潜流入渗补给量(万m3/a);Q侧入为侧向流入量(万 m3/a);Q回归为地下水灌溉回归量(万 m3/a);Q蒸发为地下水蒸发蒸腾量(万 m3/a);Q泉为泉水溢出量(万 m3/a);Q开为地下水开采量(万 m3/a);Q侧出为侧向流出量(万 m3/a);ΔQ为均衡期始末地下水储量变化量(万 m3/a)。 ΔQ＞0时,水位上升,ΔQ＜0时,水位下降。

3 月牙泉水位变化原因

月牙泉水位变化有两个方面的原因：一是自然因素,二是人为因素,其中人为因素是导致月牙泉水位变化最主要的原因,也是最直接的原因。

3.1 自然因素

对月牙泉水位产生影响的自然因素主要为泉水水面蒸发和风沙淤积。

3.1.1 水面蒸发对月牙泉湖水位的影响

根据计算,泉湖水面 1997年蒸发消耗的水量为 1.338 2万方[1]。正常情况下,月牙泉应早已干涸,主要原因得益于泉域特定的地质结构和补给来源[3],泉域地下水的主要补给来自西部党河冲洪积平原区的地下水,只要区域地下水位始终保持一定的高度,水面蒸发对泉湖水位的影响可以认为是微乎其微的。

3.1.2 风沙淤积对月牙泉湖水位的影向

敦煌地区风大沙多,有“世界风库”之称,特别是沙尘天气,满天飞沙走石,虽然月牙泉其地形与风向具有一种和谐的关系,但日积月累,湖底也会产生少量的淤泥,使月牙泉湖底变浅,从而可以塑造月牙泉的外部形态,但对于月牙泉水位不会造成影响。

综上,自然因素对月牙泉的水位的影响很小、影响程度微乎其微,难以引起泉水位在短时间内产生大幅度变化。

3.2 人为因素对区域及月牙泉水位变化的影响

3.2.1 水利工程建设对区域地下水位及泉水动态的影响

上世纪六十年代以前,区内基本上没有什么大的水利工程设施,地下水、地表水均是自然状态下发生的补给、径流、排泄过程,特别是党河在祁连山大量冰雪融水和降雨的补给条件下,党河河床长年流水不断,由于河床下部多分布为松散的砂砾石层,河水在径流过程中产生大量的渗漏,为本地区域地下水提供了丰富的补给源。区域性水位普遍较高,这种区域性高水位的地下水,为月牙泉提供了具有充分保障的补给源,这也是月牙泉在这种极端干旱的条件下数千年不干涸的秘密所在。也就是早期历史时期泉水动态一直比较稳定的原因。

1975年党河水库建成蓄水,党河河水全部被截入库,水库下游河床从此处于长期断流干涸的状态。党河水库的修建和高标准输水渠道的修建,河水的断流和渗漏量的减少,使区域地下水的补给来源大大减少,地下水自然状态下的补给条件发生了巨大的变化,造成地下水总补给量的减少,导致区域性地下水位下降,并进一步对月牙泉地下水位产生影响。输水渠道的修建,代替了原来以河道流水为主的自然水流输送状态,渗入地下的水量迅速减少,渗入对地下水所产生的补给量很少,从泉域地下水均衡方程式(1)可以看出,此期间(均衡期始末地下水储量变化量)ΔQ＜0,水位下降,和图 1曲线十分吻合。这是月牙泉水位下降的重要原因之一。

3.2.2 地下水的开采利用对月牙泉水位的影响

新中国成立以来的 60年,随着经济发展、人口增长(由解放初期的约 6万人,2008年增加到 17.67万人,增长了2.3倍)、耕地面积不断增加(由解放初期的 13.4万亩 2008年增加到约 41.72万亩,增长了 3倍多),对水资源的需求日益扩大,1971年全市有机井 400多眼,1997年已达到 1 134,2007年已达到 3 179眼,地下水开采量逐年猛增。1977年区内地下水开采量 3 130万 m3,1999年地下水开采量 5 883万 m3,2007年地下水开采量达到 13 084万 m3,2007年地下水开采量比 1977年增加了 7倍多。地下水资源的开发利用,对区内工农业生产的发展起到了很大的促进作用。但是对地下水的大量超采,使得整个盆地区水资源“收支”平衡被打破,出现了负均衡,如 1997年对盆地水资源均衡结果为 -7 421万方/a,2008年均衡差为 -12 816.19万方/年,引起地下水位持续下降,泉水逐年减少。

3.2.3 月牙泉水位下降应急治理工程

敦煌月牙泉是一处十分奇特、宝贵的自然景观资源,在国内外有很高的知名度。近几十年来,由于自然和人为因素的影响,月牙泉水位不断下降,月牙泉的自然生态环境趋于恶化。拯救月牙泉成为一项十分迫切的任务。受敦煌市政府委托,甘肃省地质环境监测院于 2006年完成了《甘肃省敦煌市月牙泉水位下降应急治理工程施工图设计》。治理工程原理就是依据月牙泉补给排关系,利用人工渗水来增加地下水补给量,从而抬高月牙泉水位[4],2008年 3月敦煌市政府对部分完工渗水场进行了三个月的试运行,试运行至 6月中旬,月牙泉湖水位上升 1.80 m,达到了较为理想的效果。这次治理工程实践证明了对月牙泉水位下降原因的正确分析和判断。

综上所述,党河水库的修建,高标准输水渠道的修建和节水措施的实施,使泉水侧向补给量不断减少,地下水的利用率越来越高。敦煌盆地机井数量的增加、地下水的超采,导致了区域地下水补给量的减少、开采量的增大,1960—1997年期间地下水一直处于负均衡状态,这是这一时期区域地下水位下降的根本原因,区域地下水位的下降,又必然造成月牙泉水位的下降。因此,人为因素是导致月牙泉水位下降最直接也是最根本的原因。

4 结论

通过对月牙水位变化分析后认为,月牙泉水位变化的主要原因是党河水库的修建,高标准输水渠道的修建,敦煌盆地机井数量及开采量的增加,导致了区域地下水补给量的减少、开采量的增大,地下水长期处于负均衡状态。即人为因素是导致月牙泉水位变化最直接也是最根本的原因。

查清了月牙泉水位变化原因后,对月牙泉实施了水位下降应急治理工程,并达到了较为理想的效果。也为月牙泉区域生态地质环境保护工作可以提供理论、技术指导和科学决策依据。

[1]甘肃省地质环境监测院.甘肃敦煌月牙泉地区水文地质与环境地质综合勘查报告,2008.

[2]甘肃省地质环境监测院.甘肃省敦煌市城市环境地质问题调查评价报告,2008.

[3]尹念文.月牙泉的成因分析,地下水 2009,2

[4]甘肃省地质环境监测院.甘肃省敦煌市月牙泉水位下降应急治理工程施工图设计,2006.