基于灰色理论的地下水埋深预测分析

李 亮,陈 刚,马 峰

(中国地质大学环境学院,湖北 武汉 430074)

华北平原是地面沉降发生严重的地区之一,而地面沉降发生的主要原因是由于对地下水的过度开采。地下水位的埋深与地面沉降之间有密切的联系。通过预测地下水位的埋深可以为地面沉降的预测提供依据,同时,通过预测结果和经过地下水开采限制之后的实际埋深进行比较,从而判断采取措施后的效果。

1 灰色预测模型 GM(1,1)的建立

灰色系统理论建模的主要任务是根据系统的行为特征数据,找到因素本身或因素之间的数学关系,从而了解系统的动态行为和发展趋势。灰色系统理论认为：无规的离散时空数列是潜在的有规序列的一种表现,因而通过生成变换可将无规序列变成有规序列。也就是说,灰色系统理论的建模实际上是对生成数列的建模,而不是像一般建模方法那样采用原始数列直接建模。

灰色模型(Grey Model)简称 GM模型,是灰色系统理论的基本模型,它是以灰色模块(所谓模块式时间数列 X(m)在时间数据平面上的连续曲线或逼近曲线与时间轴所围成的区域)为基础,以微分拟合法而建成的模型。在灰色模型中,由预测值上界和下界所夹的部分称为灰色平面(简称灰平面),这个灰平面的大小是由各个未来时刻预测值的灰区间所决定的。因此,它由原点(现在时刻)向未来时刻呈喇叭型展开,即未来时刻越远,预测值灰区间就越大。这样,模型对系统的刻划将因时间的逐渐外推,而逐渐失真。为此,灰色系统理论提出了一系列调整和修正模型的方法,从而提高了模型的精度。

图1 GM(1,1)模型建模框图

GM(1,1)灰色模型是将离散的随机数经过一次累加生成算子(记为 1-AGO;Accumulating Generation Operation),弱化其随机性,使平稳性增加,得到较有规律的生成数,然后建立白化式微分方程。解方程进而建立模型。

设研究对象的原始数列为：

由于这种时间序列多为随机的,不能直接处理,因此,对数列作一次累加生成算子(记作 1-AGO),即令

根据上式建立一个单序列的一阶线性动态灰色预测模型：

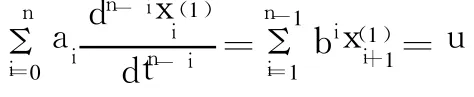
记为 GM(1,1)模型,其相应的微分方程为：

其 中 X∧(0)(1)=X∧(0)(0)

在建立模型前对数列 X(0)进行准光滑性检验,检验方程如下：

若对 t有 ρ(t)＜0.5,则其满足准光滑条件。

随后检验数列 X(1)是否具有准指数规律,检验方程如下：

若对 t有 σ(1)(t)ϵ[1,b],δ=b-1≤0.5,则准指数规律满足,可对 X(1)建立 GM(1,1)模型,否则需继续累加。

在建立模型后,还必须对模型进行精度检验,其检验标准见表 1。

表1 模型精度等级检验表

从灰色预测方法原理可知,-a为发展系数,主要控制系统发展态势的大小,即反映预测的发展态,;u为灰色作用量,其大小反映了数据变化的关系。其中：当 -a＜0.3时,GM(1,1)模型可用于中长期预测;当 0.3＜-a＜0.5时,GM(1,1)模型可用于短期预测中长期预测慎用;当 0.5＜-a＜1时,应采用 GM(1,1)改进模型,包括 GM(1,1)残差修正模型;当 -a＞1时,不宜采用 GM(1,1)模型,可考虑其他预测方法。

2 灰色预测的特点及分类

灰色预测是灰色系统理论的重要组成部分,其具有预测模型不唯一;一般预测到一个区间,而不是一个点;预测区间的大小与预测精度成反比,而与预测成功率成正比等特点。

自该方法提出以来,在社会系统、生态系统、工业生产等领域中得到了广泛的应用.这些应用包括灰色数列预测、年灾变预测、季节灾变预测、拓扑预测、残差辨识预测、系统综合预测等.这些类型的预测虽然各具特色,但就其本质而言,都是灰色 GM(1,1)模型的拓广,其基本方法是用指数曲线拟合原始点列,并由此对原始点列进行预测,预测结果精度较高但也有些预测不符合实际情况。

3 地下水水位预测

依托于“华北平原地面沉降机理与模拟模型研究”项目,根据河北沧州市泊头县东辛店乡水位观测资料统计,得出1997～2002年沧州市泊头县地下水水位埋深是呈逐年加深的总趋势,符合 GM(1,1)模型的要求,故使用 1997～2002年数据作为原始数据(见表),并对未来 1年(2003年)的水位埋深进行预测。

表2 1997年 ～2002年地下水年平均埋深 m

注：地面沉降每年是以毫米的速度发生,而地下水位的变化时以米来记,所以,由于地面沉降而使埋深值发生变化很小,可以忽略。

用 GM(1,1)模型对地下水水位埋深进行预测。

由表知,1997年 ～2002年地下水水位埋深的原始时间序列

X(0)={6.66,8.30,9.48,10.58,10.37,11.50}

由(6.3)式得一次累加数据序列

X(1)={6.66,14.96,24.44,35.02,45.39,56.89}

对 X(0)进行准光滑检验,由式(6.11)得：

ρ(2)≈1.2470,ρ(3)≈0.6336, ρ(4)≈0.4331,ρ(5)≈ 0.2962,ρ(6)≈0.2534。由于当 t＞3时 ρ(t)＜0.5,所以准光滑条件成立。

检验 X(1)是否具有准指数规律,

表3 准指数规律检验表

当 t＞3时,σ(1)(t)ϵ(1,1.5),δ=0.5,所以满足准指数规律,可建立 GM(1,1)模型。

对 X(1)作紧邻均值生成。令

z(1)(t)=0.5x(1)(t)+0.5x(1)(t-1)

得Z(1)=(z(1)(2),z(1)(3),z(1)(4),z(1)(5),z(1)(6))=(10.804 9,19.692 8,29.721 9,40.199 0,63.087 9)

于是

求参数 a和 u(使用 Excel和 MATLAB互相计算、检验得出)得：

a=-0.071 6,u=7.877 2

得到预测模型：

即 X(T)为 T年的预测水位,T为年份,T＞1997

X(T)=X(1)(t)-X(1)(t-1)

模型验证与误差分析。利用模型预测每年五灰含水层水位,并与每年实际水位进行对比得出误差检验表(见表)。

平均相对误差为 0.03＜0.05,查模型精度等级检验表得：良,可知预测精度为二级。

表4 实际值与预测值对比及误差检验表 m

与上预测过程中所得数据是使用 Excel和 MATLAB互相计算、检验得出。主要用MATLAB计算矩阵的乘积和逆,得 aˆ=(BTB)-1BTYN,即得矩阵元素 a和 u,也就是模型的参数。所得数据与灰色建模系统软件[10]计算所得数据吻合,说明计算过程无误,模型建立正确。而且预测精度较高,说明该模型适合地下水位埋深得预测。

4 结论

(1)灰色 GM(1,1)可以在数据较少的情况下进行短期预测,预测精度较高、计算简单、方法易行。但是进行长期的预测时,其精度不能保证,所以预测时间不易过长,同时用最新的数据不断的优化、更新模型。

(2)地下水位的埋深与地下水的开采量和补充量有密切的关系,可以为地面沉降的预测提供依据和参考。在华北平原进行地下水开采限制以来,地面沉降明显变缓,地下水位埋深下降的速度也变缓。所以,灰色 GM(1,1)预测结果也可以与采取措施后的实际水位埋深进行比较,从而清晰的看到所采取措施的效果。

[1]傅立.灰色系统理论及其应用[J].北京：科学技术文献出版社.1992：31-59.

[2]房佩贤,卫中鼎,廖资生等.专门水文地质学.北京：地质出版社 ,1987：202.

[3]王大纯,张人权,史毅虹等.水文地质学基础.北京：地质出版社 ,1995：61-98.

[4]贾备,邬亮.基于灰色理论的基坑沉降预测分析[J].吉林大学学报,2009：78-80.

[5]王忠桃.灰色预测模型相关技术研究[J].成都西南交通大学,2008.

[6]张沙莎.曹庄矿充水含水层地下水动态分析[D],徐州中国矿业大学,2006.