我国药品价格管理中的“政府—医院—消费者”三方博弈分析
○田坤
(武汉理工大学管理学院 湖北 武汉 430070)
药品是一种特殊商品,由于其特殊性质和功能——垄断性与福利性,导致对于药品价格的管理非常重要,备受政府、企业和国民的关注。目前,我国药品价格管理的现有模式主要有三种:市场调控、政府调控、政府调控和市场调控相结合的调控。
然而,尽管如此,我国目前的药品价格市场依然存在定价不合理、看不起病、买不起药的情况。针对这些问题,本文从药品价格市场的关键利益方——政府、医院(由于医院与制药企业都处于价格的初始决定环节,而鉴于医院在初始决定中的强势地位,价格的初始决定基本上可以由医院来说明,因此这里的医院不仅包括医院,还包括制药企业)、消费者出发,构造出三方博弈模型,来分析药品市场的价格问题。
一、博弈模型的建立及各参与者的收益结构分析
在博弈中,各个参与者的的行为不是单一的,而是有一定的选择的。假定医院有两个决策(这两个决策都是静态的,医院自身知道,但消费者不知道,政府通过价格审查后可能知道):价格虚高(Hh)及价格正常(Nh)。对于医院来说,它没有把价格降低的激励,因为价格降低在处方一定的情况下利润会减少。而消费者也有两个决策(这两个决策表面上看是静态的,但由于能容易地转化为动态决策,因而实质上是动态决策):认为价格虚高(Hc)及认为价格正常(Nc)。如果消费者认为价格虚高,其必然会通过一定渠道使政府(包括药监局、医疗保险机构、代表消费者利益的协会等为代表)对药品价格进行审查;如果消费者认为价格正常,则会接受价格。政府有两类决策,一类是审查决策:审查(E)及放弃(G),即政府可能通过一些机构对药品价格进行审查,当然也有可能放弃审查;另一类是政府决定审查后的客观决策:查出价高(E+)及未查出价高(E0)。需要注意的是在价格正常状态下政府是查不出价格虚高的,即此时P(E+)=0,P(E0)=1。现将各种情况分别做分析(需要说明的是文中的各方收益是以正常价格为基准的)。
1、第一种情况。如果价格确实过高,即医院在零售价格中为图私利而人为使价格虚高,此时,若消费者也认为价格虚高,且政府着手进行审查,如果查出价高,各收益情况如下:医院因原来价格非正常高而产生的额外收益变成0,同时由于政府审查的成功,政府会对其施以一定的罚金F,因此医院的净收益为-F;消费者由于价格得以控制需要额外支付的成本变成0,但由于消费者维护自己的权利需要对政府及其机构进行活动,因而需要支付一定的成本,用交易成本来表示,记为CS,因而消费者的净收益变成-CS;政府审查的成本用稽查成本CC表示,同时获得罚款F,则政府的净收益为F-CC。
2、第二种情况。如果价格事实上偏高,消费者认为价格亦偏高,且政府对价格进行审查,但是审查未查出价格高,各收益情况如下:医院获得价格非正常高产生的额外收益R,但R中的一部分tR会以税收的形式上缴给政府,其额外净收益为(1-t)R,净收益也为(1-t)R;而消费者由于审查失败使价格并未改变,必须支付价格过高带来的额外成本R,但由于医疗保险机构的存在,这部分成本并不是全部承担,而只会承担(1-θ)R,θ表示政府医疗分担系数,同时消费者要支付交易成本CS,因而其净收益为-(1-θ)R-CS;政府一方面会获得医院向政府缴纳的药品税收tR,但同时会因为社会医疗保险的存在承担θR的额外成本,同时还为审查付出稽查成本CC,因而净收益为tR-θR-CC。
3、第三种情况。如果价格事实上偏高,消费者认为价格亦偏高,但政府不对价格进行审查,此时,各参与者收益情况如下:医院的收益同情形(2),其净收益为(1-t)R;消费者由于采取了努力但努力失败,结果对于消费者来说与说服政府并且政府审查失败一样,其净收益为-(1-θ)R-CS;但对于政府来说两种情况是不一样的,因为政府不需要支付审查过程中产生的稽查成本CC,其净收益为tR-θR。
4、第四种情况。如果价格事实上偏高,但消费者认为价格正常,此时,各参与者收益情况如下:医院的收益与情形(2)、(3)同,净收益为(1-t)R;由于消费者不试图去说服政府,因此无需支付交易成本CS,因而其净收益为-(1-θ)R;而政府的净收益与情形(3)同。
5、第五种情况。如果价格事实上是正常的,即医院未就私利而谋取额外收益,且消费者信为药品价格是正常的,此时,各参与者收益情况如下:由于价格正常医院并无价格偏高带来的利润,因而其净收益为0;同样消费者与政府也未因此而付出成本,因而消费者与政府的净收益皆为0。事实上这个状态是一个市场出清的状态,各市场参与者达到了均衡。
6、第六种情况。如果价格事实上是正常的,但是消费者认为价格存在着虚高的状况,但政府不对价格进行审查,此时,各参与者收益情况如下:医院在这个过程中未得到任何额外收益,也未支付任何额外成本,其净收益为0;而消费者由于主观上的价格认识会对政府施加影响而造成交易成本CS,其净收益也为-CS;对于政府来说不发生其他成本与收益,其净收益为0。
7、第七种情况。如果价格事实上是正常的,但是消费者认为价格存在着虚高的状况,且政府对价格进行审查,但在这种情况下,审查的结果肯定是未查出高价。此时,各参与者收益情况如下:医院的净收益为0;消费者付出了交易成本CS,其净收益为-CS;政府付出了稽查成本CC,其净收益为-CC。三方博弈构成的博弈矩阵可以用表1表示。
对于博弈来说,其分析一般从两个方面进行,其一就是静态博弈,即进行一次博弈得出均衡结果,这种博弈结果可能有多种;其二是动态博弈,即进行多次博弈得出的结构,这种博弈有可能有多个解,有可能一个解,也有可能无解。
二、静态博弈结果分析
1、医院博弈行为分析。医院的博弈行为是根据政府与消费者的行为具体做出的,要找出其博弈行为的均衡概率,就必须相应地对政府的行为进行分析。
首先分析消费者的行为。消费者的选择在于主观的想法(这些想法能够产生实际行动)对自己收益的影响,当其想法对收益无影响时,则达到了均衡。
消费者认为价格虚高给消费者带来的期望收益为:
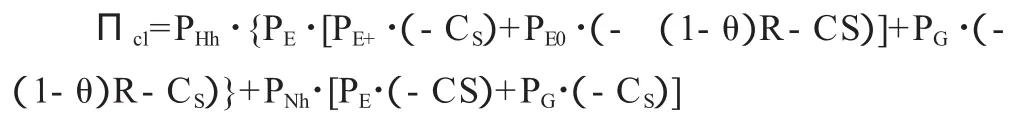
消费者认为价格正常带来的期望收益为:
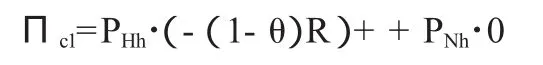
当两种想法带来的期望收益相同时,可解出医院的均衡概率(此概率为医院通过人为途径使价格上升的概率,即价格虚高概率):
从Пc1=Пc1得:
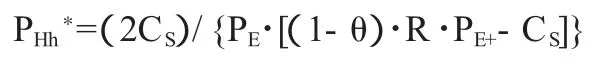
再来分析政府的行为对医院的影响。在对政府进行分析的时候,只需要对政府的审查决策进行分析,因为审查成功的概率与政府的客观行为能力、管理水平、经济水平有很大关系,这个概率基本上是客观概率,非人为决定,因而不做分析。
政府认为审查所带来的期望收益为:
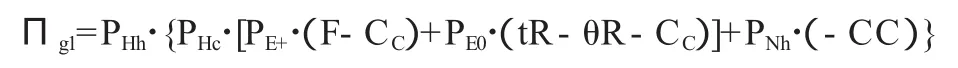
政府认为不审查即放弃的期望收益为:
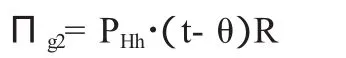
令Пg1=Пg2,然而从数学上来说这个方程有无穷多个解,找不出一个均衡的解,因此,这是一个非博弈均衡。

表1 “政府—医院—消费者”三方博弈矩阵
2、消费者博弈行为分析。与对医院的分析类似,消费者的行为与政府以及医院的行为有十分密切的关系。现将两个参与者的行为进行分析。
首先分析医院的行为。医院价格虚高(即医院人为的价格提高)期望收益为:
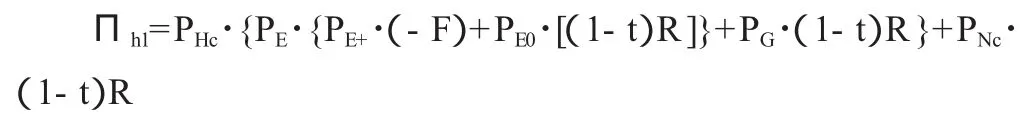
医院对价格不做改变(即价格正常)的期望收益为:
Пh2=0
医院对决策漠然之时,即两种决策对于医院来说都无差别之时,可得消费者决策的一个均衡概率。令Пh1=Пh2,解出:
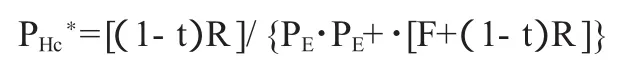
再分析政府的行为。政府认为审查所带来的期望收益为:
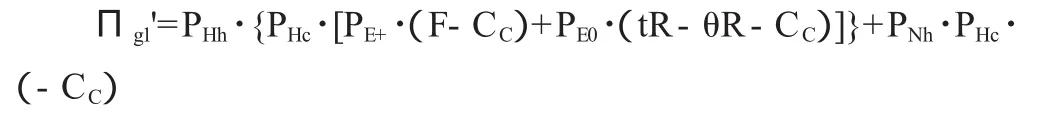
政府认为不审查即放弃的期望收益为:
Пg2'=PHh·PHc·(t-θ)R
对于政府来说,审查与不审查只有当两者的期望收益相等时才会无差别。令Пg1'=Пg2',在计算中发现数学上这个方程存在无穷多解,找不出一个均衡解,因而在这种情况下不存在博弈均衡,而是一个非博弈均衡。
3、政府博弈行为分析。由于不需要对审查成功的概率作何分析,因而基本上审查成功概率是一个已知数。政府的博弈行为分析主要是求出其进行审查与否的决策概率。与医院和消费者的行为分析相同,采用等收益分析。
首先分析消费者的决策。消费者在选择对价格进行否定的时候,其期望收益为:

消费者认为价格正常带来的期望收益为:
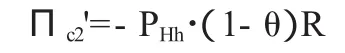
取 Пc1'=Пc2',则有:
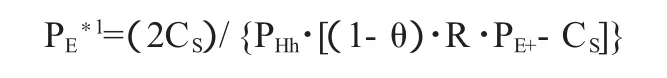
再次分析医院的决策对政府的影响。医院做出导致价格虚高的期望收益为:
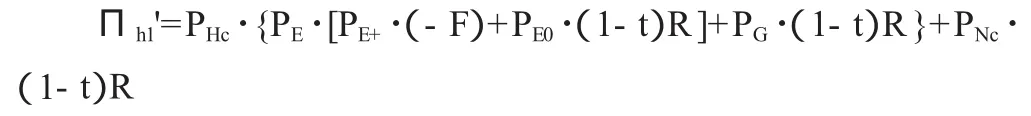
医院不对价格做出改变的期望效用为:
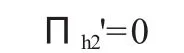
令 Пh1'=Пh2',则有:
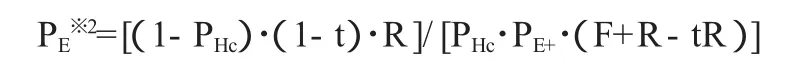
4、静态博弈结果总结。从分析中可以看出,任何一个博弈参与者的行为都与其他参与者的行为分不开。而从结果上来看,静态博弈有两种结果,而在每一种结果中,在静态博弈的范围内都达到了均衡。那么这几种结果的结构如下:
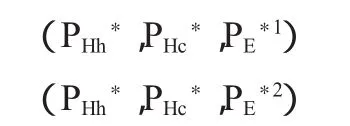
三、动态博弈结果分析
动态博弈与静态博弈不同在于,博弈过程基本上不会在第一次结束,各方会依次改变博弈决策,并且这个博弈决策会参考博弈中已知的参数。在这种情况下,这基本上已经是一个混合博弈的过程,其均衡不单是找出期望收益的交错点,而是在收益最大化的条件下寻求最优解。
因此,在求解中,首先要找出各参与者的期望收益而不是在各个决策下的期望收益,而这个期望收益是与其他参与者的决策概率有关,因而这个期望收益实际上与其他参与者的期望收益有关,构建完期望收益后,就要进行交叉求解。
首先对医院进行分析。医院的期望收益可表示为:
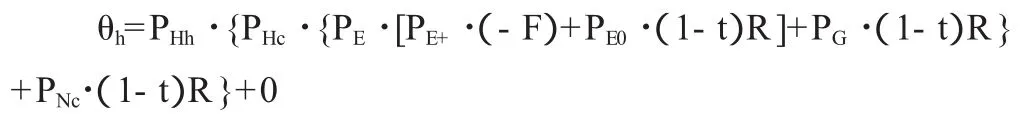
再求消费者的期望收益:
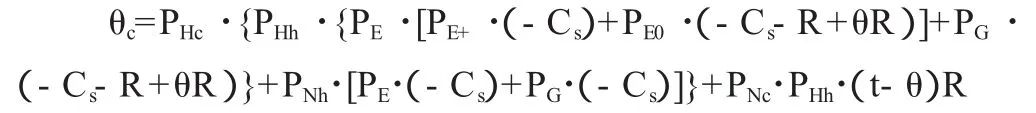
而政府的期望收益为:
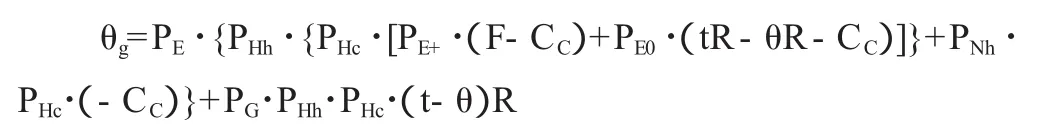
动态博弈在数学上的主要目的就是看是否有均衡解,有几个解。而三个参与者能够决策的只能是自己的行为,因而为了使自己的期望收益达到最大,参与者选择自己的决策都是非常有效率的。但这个效率是经过多次博弈而产生的。现就三个期望收益分别对 PHh、PHc、PE求导,得:
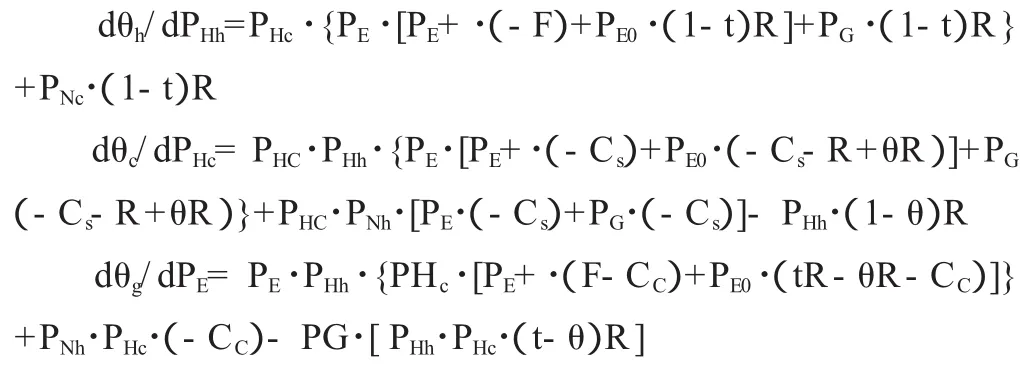
令三个导数等于0,即为三个参与者的期望收益最大化的一阶条件,则构成一个线性方程组:
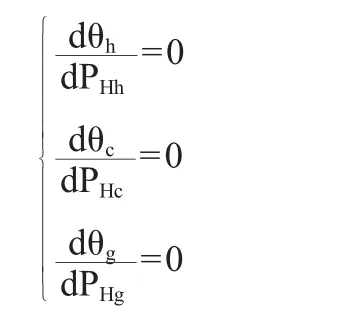
解这个方程组,得:
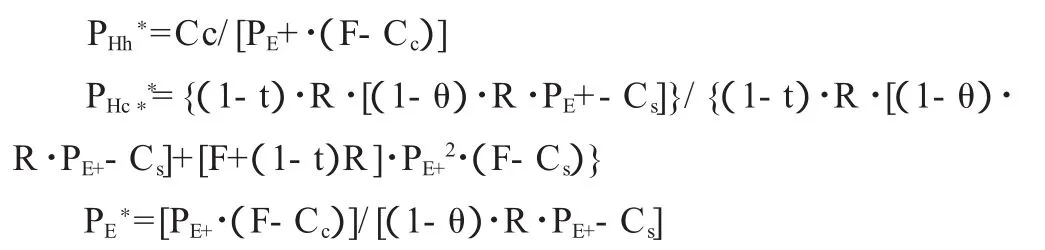
四、结论
从结果上来看,动态博弈只有一组均衡解,这与静态博弈的结果不同,且这个解与静态博弈在形式上也大不相同,这个解并不与其他参与者的先验概率有关,只与在博弈中的已知参数有关。从解的性质来看,医院使价格虚高的概率是与消费者的交易成本Cc成正向辩证关系的,与稽查成功的概率以及政府查出价格过高后对医院的罚款成反比。由于政府在博弈中的主要行为是对医院进行稽查,因而其主要看其对医院构成影响的方式。由博弈结果可以得到:提高消费者的申诉效率,降低交易成本,同时提高政府效率使稽查成功的概率增大,并且适当提高政府对违规医院的处罚力度,可以有效地控制价格上涨行为。
[1]张维迎:博弈论与信息经济学[M].上海:三联书店,1996.
[2]姚国庆:博弈论[M].北京:高等教育出版社,2007.

