一种新型谐振腔增强型光电探测器的性能分析

赵维

（渭南师范学院计算机科学系，陕西渭南714000）

随着光波分复用（Wavelength Division Multiplexing，WDM）通信技术的发展，具有波长选择特性和高响应速度的光探测器已经在光通信中显示出了它的巨大优势。这里探讨一种新型的光电探测器——谐振腔增强型光电探测器（Resonant Cavity Enhanced Photodetector，RCEP），该RCEP的基本结构是将吸收层插入到谐振腔当中。由于谐振腔的增强效应使其在较薄的吸收层情况下即可获得较高的量子效率，同时减少了光生载流子在吸收层的渡越时间，提高了器件的响应速度，因而能够解决传统探测器量子效率和响应速度之间的相互制约矛盾。此外，由于谐振腔的作用使该器件本身具有波长选择特性，无需外加滤波器[1]，因而有可能成为波分复用光纤通信系统中的新一代光探测器。

1 RCE器件的结构及量子效率分析

量子效率是用来表征光电转换效率的物理量，定义式为

式中，Lp是光生电流强度，E0是电子电荷，P0是入射光强度。

图1为RCE器件的结构原理图。图中，吸收区是一种窄禁带的半导体材料，顶部与底部的DBR由交替的非吸收的宽禁带材料构成，吸收区与顶部DBR和底部DBR之间的隔离区也为宽禁带材料。在实际应用中，器件的反射镜一般由介质或半导体材料的1/4波长堆栈构成，简化设计时，顶镜可以利用半导体材料和空气的界面构成，提供约30%的反射率。吸收层间插在两个端面反射镜之间，其厚度为d，吸收系数为α。吸收层与器件的顶镜和底镜间的间隔由L1和L2表示，其材料吸收系数由αex表示。顶镜与底镜的场反射系数分别为r1e-iψ1和r2e-iψ2

，其中ψ1、ψ2表示由于光场透射反射镜而引起的相位偏移[2]。入射光波电场分量Ei的透射部分等于t1Ei。谐振腔内的前向传输波电场分量Ef即由上述透射分量及腔内反射组成。

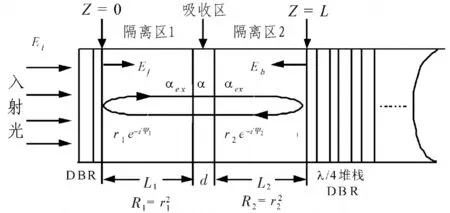
图1 RCE探测器的结构分析模型

图1中z=0处的前向传输光场Ef可以通过自洽得出，即Ef是入射光波的透射分量及其在腔内的反馈之和：

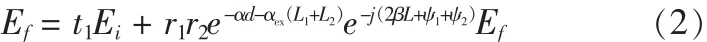
逆向传输波（即z=L处的Eb）可以通过计算前向传输光波经腔镜的反射得到：

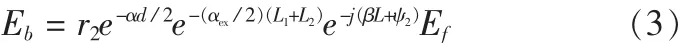
此时，有源区吸收光功率（Pl）可以从入射光功率Pi得到：

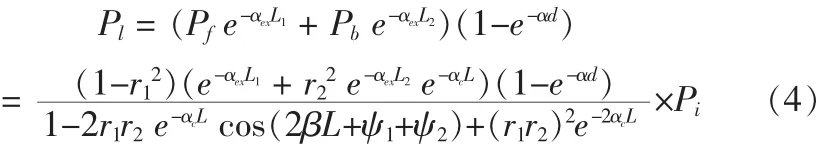
假设所有光生载流子均对探测器电流有贡献，则η即是吸收光功率与入射光功率之比值，即η=Pl/Pi，可得出：

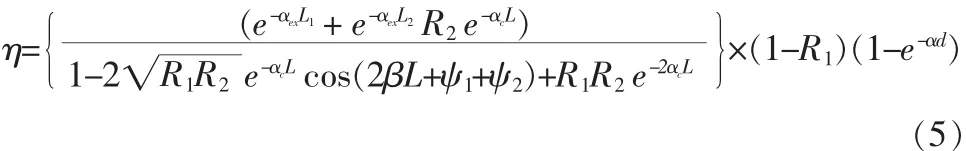
式中，αc=（αexL1+αexL2+αd）/L。

在实际的探测器设计中，有源层以外的材料（αex为5～10 cm）对光的吸收（主要来自自由载流子吸收）与有源层（α≥104 cm）相比可以忽略，所以式（5）中的αex可以忽略不计，这样η为：

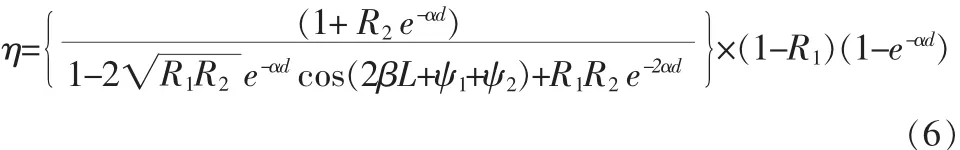
式（6）右侧大括号内的参数代表了腔的量子效率增强效应，当R2=0时该增强因子为1，此时式（6）给出的是传统探测器的量子效率。图2显示了η对波长的依赖关系。三条曲线分别对应于顶镜反射率R1为0．9，0．3和0．05时的情况（其中实线为－0．9，点线为－0．3，段线为－0．05），其余参数设定为底镜反射率R2=0．9，αd=0．1，L=2 μm。η周期性地在谐振波长处，即2βL+ψ1+ψ2=2mπ（m=1，2，3．．）得到增强。

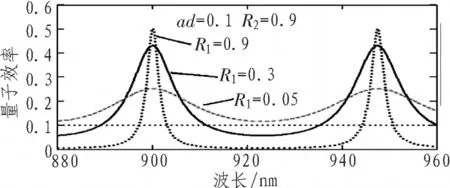
图2 RCE器件量子效率在顶镜反射率变化下的波长依赖性特性

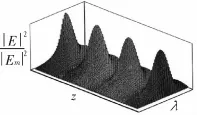
图3 RCE器件中的基于光波长的光场分布特性

图2中的平直虚线即代表在相同有源层厚度（αd=0．1）情况下传统光探测器所能达到的量子效率，两种探测器的对比是很明显的。传统光探测器在很宽的波长范围内具有基本恒定的量子效率，最大量子效率也不超过0．1[5]，而RCE型光探测器可以通过设计在特定波长处获得极大增强的量子效率。这就是谐振腔对量子效率的增强作用[3]。

RCE器件的量子效率最大值条件为：R1=R2e－2αd，恰当地选择器件参数可以使RCE PD的量子效率达到近乎100%的理论值。

2 RCE器件的驻波效应分析

对于两个相向传播的光波方程式（2）和式（3），它们相互叠加形成的驻波将会在腔内形成光场强度的周期性空间分布，器件量子效率由于受到光场强度分布的影响，将是有源层在光场中位置的函数，称为驻波效应（Standing Wave Effect，SWE）[6]。正是SWE的存在使得RCE器件具有波长选择性和谐振波长处的增强效应。

驻波效应在量子效率公式中可以方便表示为有效吸收系数αeff=SWE·α，它随有源层位置的不同而表现为增强或减弱效应。

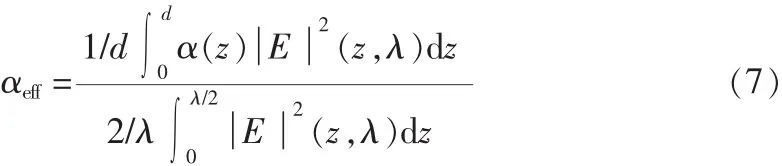
假设吸收区之外的吸收系数可忽略，而吸收区的吸收系数为常数，则：

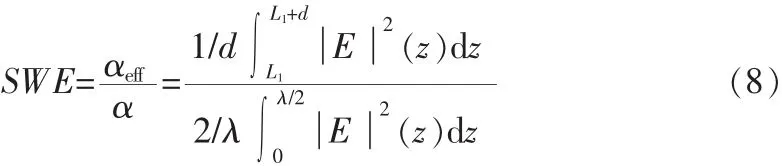
腔内驻波的前向分量（Ef）与后向分量（Eb）由式（2）和式（3）给出，总电场E及其强度为：

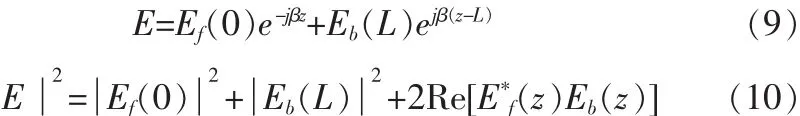
将式（2）和式（4）代入式（10），并假设α=0，得：

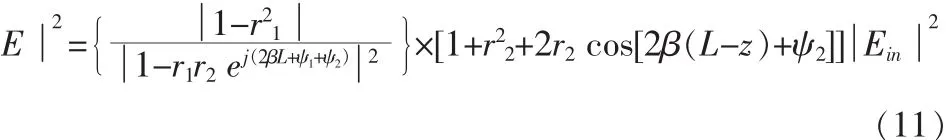
图3所示为基于GaAs材料的RCE光探测器由式（11）计算得出的依赖于光波长的腔内光场强度分布，可以看出RCE器件内部光场强度随位置和波长呈现周期性变化，显示出驻波效应的影响。

将式（11）代入式（8），略去与波长无关的因子，得到驻波效应与谐振腔参数的关系：

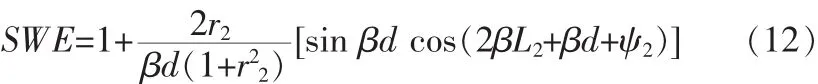
图4（a）波长显示了SWE在不同有源层厚度时对波长的依赖关系。d≈λ0/4n（实线）时，SWE在0．35到1．7之间变动，这使得器件对不同波长的光响应有剧烈的变化。当d≈λ0/2n（虚线）时，驻波效应较为微弱，这是因为有源层覆盖了整个的半周期。其中器件的底部反射镜由20个周期的GaAs/AlAs DBR构成，顶部反射镜由本征GaAs与空气界面充当，（L1=L2=2 μm）。对于一个理想的底部反射镜（r2=1，ψ2=0）和实顶镜反射率（ψ1=0），L1=L2（有源层居中），驻波效应可简化为：

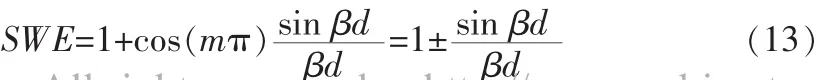
式中，±对应于有源层中心位于驻波最大和最小处的情况。SWE的极端情况如图4（b）标准化活动层厚度所示，该图也显示出了当有源层越来越厚时，SWE的作用也逐渐减小。

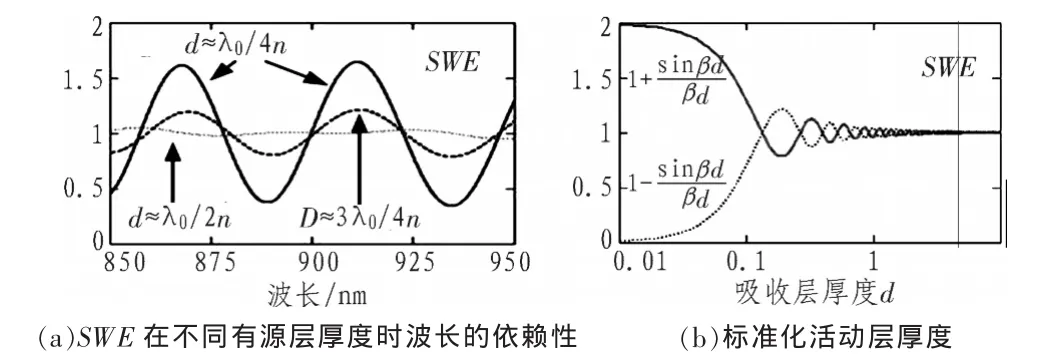
图4 驻波效应对波长及吸收层厚度d的依赖性

3 RCE器件的波长选择特性分析

对于RCE器件，在非谐振波长位置（例如：2βL+ψ1+ψ2=（2m+1）π，m=1，2，3…），腔内光场的幅值将由于前向与后向光波相消干涉的影响而减小，因而RCE器件只在其谐振波长附近很窄的范围内具有高量子效率，从而表现出波长选择特性[4]。

4 结束语

这种谐振腔增强型光探测器将光学滤波器和光电探测器通过F-P微腔巧妙地集成在一起，其独特结构解决了普通光探测器量子效率与载流子渡越时间相互制约的问题，使其在量子效率和响应速度方面获得很大改进。其具有的波长选择特性，使这种新型器件可广泛应用于包括光探测器、光调制器、发光二极管等多种光电器件。

[1]BnlüS，St rite S.Resonant cavity enhanced photonic devices[J].J.Appl.Phys，1995，78（2）：32-34.

[2]Jervase J A，Zebda Y.Characteristic analysis of resonant cavity enhanced（RCE）photo detectors[J].IEEE J.of Quantum Electron，1998，34（7）：25-27.

[3]Selim M，Unlu，et al，Resonant cavity enhanced photonic devices[J].Appl.Phys，1995，78（2）：55-56.

[4]Tung H H，Lee C P.Design of a resonant cavity enhanced photodetectorforhighspeedapplications[J].IEEEJ.ofQuantum Electron，1999，33（5）：30-31.

[5]顾聚兴.用于傅里叶变换红外光谱学的光电探测器[J].红外，2006，5（10）：26-27.

[6]雒伟伟，黄永清.一种改进光探测器高速性能的新方法[J].光电子.激光，2009（5）：50-52.