半捷联式稳定平台隔离度影响因素分析
胡 洋 ,彭晓乐,王宏宇
(西南技术物理研究所四川 成 都 6 10041)
导引头探测器平台的稳定方式有多种,包括动力陀螺稳定、速率陀螺稳定[1]、半捷联陀螺(导弹陀螺)稳定。其中速率陀螺稳定平台以其较高的稳定精度和具有较大的带宽而在战术导弹中获得广泛应用。但对于导引头低成本、小型化、智能化的发展需要,直接采用速率陀螺稳定方式受到限制,为此提出采用半捷联稳定方式来解决探测器平台稳定问题。
半捷联式稳定平台取掉了与稳定平台框架固联的角速率陀螺。优点是系统结构紧凑,减小了导引头的体积,降低了成本,在限定的战术技术条件下有较好的精度。半捷联式稳定平台是一种“数字平台”,捷联惯性测量单元置于框架基座上,直接测量弹体扰动,得到弹体的角速度信息,并送入数字信号处理器,捷联稳定算法然后驱动框架相应的伺服控制环对弹体运动进行补偿[2]。
半捷联式稳定平台利用导弹自动驾驶仪的高精度陀螺传感器信息,通过解算得到稳定探测器光轴指向的伺服控制指令,使同一惯性器件既可以用于平台的稳定,又可以为飞行控制系统提供稳定与控制需要的弹体角速率信息。但由于半捷联式平台探测器光轴上没有惯性测量元件,无法直接测定探测器光轴相对惯性空间的角速度信息并构成反馈来隔离弹体对光轴的扰动;同时失去了直接测定视线角速度的能力[3],只能提供弹体坐标系和平台框架坐标系内探测器相对目标位置即视线角的测量数值。
针对上述情况,针对影响半捷联稳定平台隔离度的因素作了理论分析,并进行数学仿真,结合仿真数据得出各因素的影响程度,对实际工程设计具有一定的指导意义。
1 半捷联平台稳定方案
目前在我国,半捷联稳定已用于车载寻北仪、火炮瞄准线稳定等陆上设备中,但在弹上应用还很少。对该领域的研究[4]也是从近十年才开始的,而在国外,半捷联稳定技术已在弹上应用,如美国的AIM-9X空空导弹、德国的KEPD-350“金牛座”防区外空地导弹等,其中具有代表性的就是“金牛座”防区外空地导弹,它的导引头外观如图1所示,采用航向/俯仰的机械结构,省去了横滚框。基于两框架结构对半捷联稳定方案进行误差因素分析。

图1 KEPD-350“金牛座”防区外空地导弹导引头
半捷联系统坐标转换原理为:弹体坐标系O1x1y1z1:坐标原点O1取在导弹的质心,O1x1轴与弹体几何纵轴重合,指向弹头方向为正;O1y1轴在弹体纵向对称平面内,与O1x1轴垂直,向上为正[5];O1z1轴垂直于O1x1y1平面,其方向按右手定则确定[6]。
光轴坐标系O2x2y2z2:与稳定平台内框固联,坐标原点O2取在探测器靶面中心,在稳定平台各框均处于零位时,光轴坐标系O2x2y2z2与弹体坐标系O1x1y1z1重合。内框为航向框,外框为俯仰框。
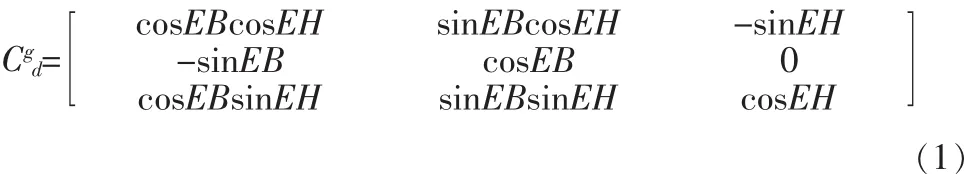
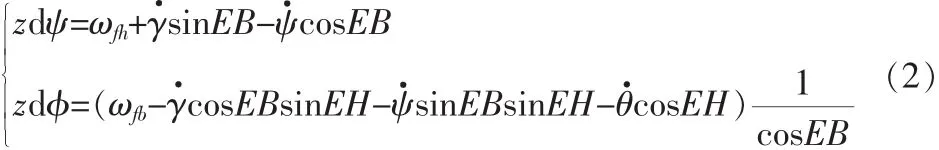
送给飞行控制系统的视线角速度:
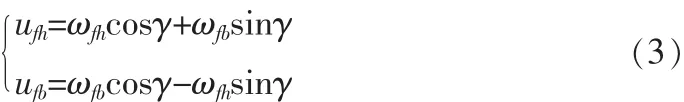
2 半捷联平台隔离度影响因素分析
影响半捷联稳定平台隔离度的因素主要有:1)半捷联坐标转换计算误差;2)平台转动干扰力矩,包括转动摩擦力矩以及导线扭转力矩等;3)平台框架角测量元件的角度测量误差,包括测量偏差和测量器件非线性误差;4)角速度测量元件或角度测量元件与微分滤波环节测得的角速度量误差;5)角度/角速度测量元件及捷联陀螺数据刷新延时导致的误差。
2.1 捷联坐标转换对平台隔离度的影响
在不计入其他各项误差因素的情况下,取一组典型弹体姿态扰动进行仿真:幅度(deg)/频率(Hz);航向:0.5/1,0.3/1.3,0.1/1.6,0.1/2;俯仰:0.5/0.8,0.6/1,0.2/1.3,0.2/1.5。仿真结果如表1所示。
2.2 平台框架转动力矩对平台隔离度的影响
在不考虑其他误差影响因素的情况下,引入框架转动干扰力矩,取典型弹体姿态扰动进行仿真,仿真结果如表2所示。

表1 捷联坐标转换对平台隔离度的影响

表2 平台框架转动力矩对平台隔离度的影响
2.3 框架角测量元件对平台隔离度的影响
2.3.1 框架角测量元件零位测量偏差对平台隔离度的影响
将框架运动主令计算公式中的EB用EB+△EB代替,EH用EH+△EH代替,分别得到其中△EB为俯仰角度零位测量偏差,△EH为航向角度零位测量偏差。于是转换误差表示为:

为简化分析过程,令弹体坐标系三轴扰动角速度大小相等且wfh=wfb=0,于是可以考查转换造成的角速度误差相对于弹体扰动角速度的比例:
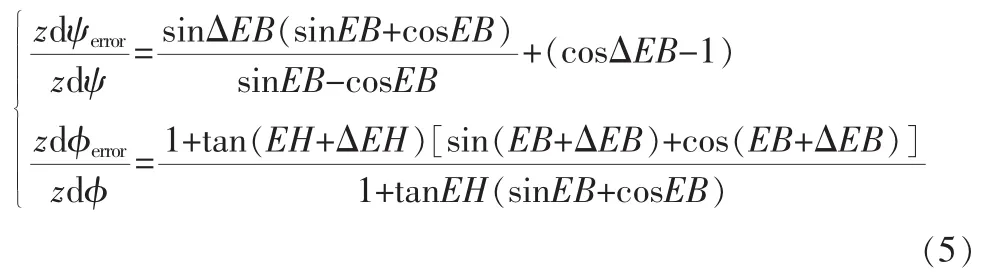
同时通过对式(5)的分析可知,弹体角速度的符号变化都能够等效为EB或EH的符号变化,只是计算结果需反号,所以只需分析一种符号下的弹体扰动角速度即可。可得在框架运动范围内(航向框架角-18°~+18°、 俯仰框架角-82°~+17°)框架角零位测量偏差导致角速度误差比例如表3所示。

表3 平台框架转动力矩对平台隔离度的影响
由表3可得:框架角速度指令误差大小除了取决于框架测角误差以及稳定平台框架角,还取决于弹体的扰动大小。当航向俯仰框架均位于活动范围以内,且测角误差为±0.2°时,角速度误差与弹体扰动的比值范围,航向为-0.605%~+0.604%,俯仰为-1.27%~+1.27%。
2.3.2 框架角测量元件非线性对平台隔离度的影响
将框架运动主令式(5)中的EB用EB×(1±0.2%)代替,EH用EH×(1±0.2%)代替,分别得到其中ΔEB为俯仰角度测量误差,ΔEH为航向角度测量误差。转换误差为:

为了简化分析过程,令三轴的弹体扰动角速度大小相等且ωfh=ωfb=0,于是可只考查转换导致的角速度误差相对于弹体扰动角速度的比例:

表4为在框架运动范围内框架角非线性测量偏差导致角速度误差比例。由表4可得:框架角速度指令误差大小除了取决于框架测角误差以及稳定平台框架角,还取决于弹体的扰动。在航向、俯仰框架活动范围以内,且测角误差为±0.2%时,角速度误差与弹体扰动的比值范围航向为-0.151%~+0.151%,俯仰为-0.291%~+0.290%。

表4 平台框架转动力矩对平台隔离度的影响
2.4 采样延时对平台隔离度的影响
角度传感器选用电位计,在数学仿真中以比例环节加采样延时环节表示。采样频率为1 kHz,即延时1 ms。对伺服模块进行仿真,模型如图2所示。
采样延时会给控制信号引入高频噪声,所以需要设置低通滤波器对捷联计算模块计算输出的平台伺服控制指令进行低通滤波。捷联陀螺的数据刷新率若为200 Hz,延时时间为5 ms,平台伺服控制指令经滤波处理后,数据刷新延时对导致平台隔离度的影响如表5所示。由表5可知陀螺数据刷新率对隔离度影响较大。
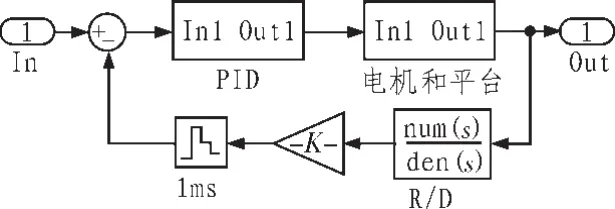
图2 伺服模块仿真模型

表5 数据刷新延时5 ms系统的隔离度
捷联陀螺的数据刷新率提高到400 Hz时,延时时间为2.5 ms,电位计采样延时不变,平台伺服控制指令经滤波处理后,数据刷新延时导致平台隔离度变化如表6所示。由表6数据可知捷联陀螺数据刷新率对平台隔离度影响较大,降低测量数据刷新延时可提高平台隔离度。
2.5 角速度测量误差对平台隔离度的影响
在伺服模块速率反馈环节添加白噪声模块作为反馈环节测量误差量,由于白噪声经微分环节后会导致系统发散,故将速率反馈回路中的数值微分环节与机械积分环节对消,以正弦信号发生器模拟捷联模块解算出的平台私服控制指令信号,图3对伺服模块进行数学仿真,表7为角速度测量误差导致隔离度。
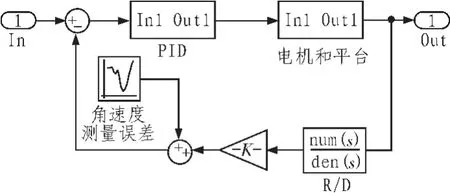
图3 伺服环节仿真模型添加角速度测量误差量

表6 数据刷新延时2.5 ms系统的隔离度

表7 角速度测量误差导致隔离度
伺服角速度量反馈误差对平台隔离度的影响和误差量基本成正比关系与弹体扰动关系不大,当弹体扰动和速度反馈误差量级相近时,将导致平台隔离特性很差。
3 结论
分析上述仿真结果可得知:1)坐标转换对稳定平台隔离度影响较小;2)平台框架转动干扰力矩对稳定平台隔离度有一定影响,应在结构设计中进行优化并提高加工工艺尽量减小转动干扰力矩,同时适当增大平台伺服环节PID比例控制系数,提高稳定平台抗干扰力矩能力;3)框架角位置测量元件精度对稳定平台隔离度有一定影响,且零位测量偏差影响程度比元器件非线性测量误差影响程度要大,故在平台设计时应注意选用线性度好的测量元件,并着重减小安装误差以降低零位测量偏差;4)采样延时对稳定平台隔离度影响较大,选用较高数据刷新率的陀螺测量元件并对平台伺服控制指令信号进行滤波可以提高平台稳定精度;5)角速度反馈测量误差对稳定平台隔离度影响较大,且与弹体扰动关联不大,故可以对角速度测量误差生成机理建模进行误差补偿。
[1]张聘义,祁载康,崔莹莹.一种匹配滤波方法在导引头捷联稳定平台中的应用研究[J].红外技术,2005,27(1):19-21
[2]周瑞青,吕善伟,刘新华.弹载捷联式天线平台两种稳定实现方法的比较[J].系统工程与电子技术,2005,27(8):32-35.
[3]周瑞青,吕善伟,刘新华.捷联式天线平台的角跟踪系统设计[J].系统工程与电子技术,2003,25(10):16-18.
[4]毛峡,张俊伟.半捷联导引头光轴的稳定性研究[J].红外与激光工程,2007,27(1):22-23.
[5]孟秀云.导弹制导与控制系统原理[M].北京:北京理工大学出版社,2003:24-25.
[6]祁载康.制导弹药技术[M].北京:北京理工大学出版社,2002:280-380.

