我国物价波动走势的实证分析——基于马尔可夫链模型的研究

《近期我国物价波动趋势的分析与预测》课题组

(湖南大学 经济与贸易学院,湖南长沙 410079)*

一、引言

物价是经济运行状况的晴雨表,准确把握物价波动趋势对于了解整个经济运行状况及其发展趋势具有非常重要的作用。因此,物价问题一直是经济学家和政策制定者所关注的焦点。自2004年开始,我国消费者价格指数(CPI)开始有所抬头,并从2006年中期呈现加速上扬的态势,2007年CPI月度同比上涨幅度又屡创历史新高,2008年2月CPI月度同比增长率高达8.7%。受国际金融危机影响,2008年下半年我国物价水平开始有所下滑,2009年2月CPI月度同比上涨幅度为-1.6%,随后物价水平持续走低,直到2009年11月CPI月度同比上涨率才由负数变为正数。短时间内物价的大幅度波动,给国民生产和人民生活带来很多不利的影响,已引起社会各界的强烈关注。尤其是物价上涨导致通货膨胀,它会给经济生活带来巨大的负面影响,加剧收入分配不公,进一步扩大居民收入差距,首当其冲的是低收入阶层利益受到巨大损害,实际生活水平较大幅度下降[1,2]。同时,物价持续下跌导致通货紧缩,也不利于经济的健康发展。今后物价走势如何,继续成为人们和政府关注的一个焦点。因此,分析与预测近期我国物价波动趋势,防止物价的大起大落,对于促进我国经济持续稳定发展、保证人民生活安定无疑具有重要的现实意义。

二、马尔可夫链模型介绍

某一时间序列在tn时刻的状态只与tn-1时刻的状态有关,而与tn-1时刻以前的状态无关,就称这一时间序列是马尔可夫链过程。用数学语言表达就是,设时间序列Zt,t∈T的状态空间S是一整数集,若对S中的任意n个整数:Si,Sj,Si1,Si2,…,Sin-2和T中任意n个整数(0≤t1＜t2＜…＜tn)都有:

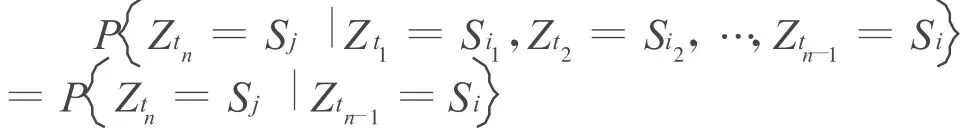
则称时间序列Zt,t∈T是具有马尔可夫链性质的随机过程[3]。其中,条件概率P{Ztn=Sj|Ztn-1=Si}称为由tn-1时刻状态Si到tn时刻状态Sj的状态转移概率,记作pij(tn-1,tn)①。分别计算出各个状态之间相互转移概率后,就可以构建一个n×n的状态转移概率矩阵其中运用马尔可夫链模型分析经济问题,其基本的步骤如下:

(1)证明时间序列变量是否是具有马尔可夫链性质的随机过程。

(2)构造状态并计算相应的状态转移概率。

(3)建立状态转移概率矩阵并计算各个状态的持续期。

(4)运用状态转移概率矩阵进行预测分析。

三、实证分析

(一)物价变动的马尔可夫性质证明

为了保证本文研究结果的正确性,在运用马尔可夫链模型分析物价波动趋势规律前,需要验证物价变化过程是否具有马尔可夫链性质,如果具有马尔可夫链性质,才能运用马尔可夫链模型分析物价波动趋势。关于物价变量的指标,本文选取消费者价格指数(CPI)增长率、生产者价格指数(PPI)增长率、商品零售价格指数(RPI)增长率、原材料、燃料和动力购进价格指数(RMPI)增长率四个指标来衡量物价波动走势。CPI、PPI和RMPI数据样本空间为1997年1月至2009年11月,有155个样本。RPI数据样本空间为1997年1月至2009年10月,有154个样本。CPI、PPI、RPI和RMPI数据均来源于国家统计数据库。

根据表1可以发现,这四个自回归方程的R2值都在0.90以上,F检验也通过了,D-W值都很接近2,这表明表1中的四个回归方程结果都是可信的。另外,在表1中可以清楚地看到:CPI(-1)和RPI(-1)的系数在1%的置信水平下是显著的,CPI(-2)、CPI(-3)与RPI(-2)、RPI(-3)它们的系数在10%的置信水平下都是不显著的;PPI(-1)和RMPI(-1)的系数在1%的置信水平下是显著的,PPI(-2)的系数在5%的置信水平下是显著的,RMPI(-2)和RMPI(-3)的系数在10%的置信水平下是显著的。这说明:t期CPI和RPI的变化只与t-1期CPI和RMPI的值有关,与t-2、t-3期的值都无关;t期PPI和RMPI的变化不仅与t-1期CPI和RMPI的值有关,还与t-2期的值有关。也就是说,CPI和RPI的变化过程具有马尔可夫性质,PPI和RMPI的变化过程不具有马尔可夫性质。

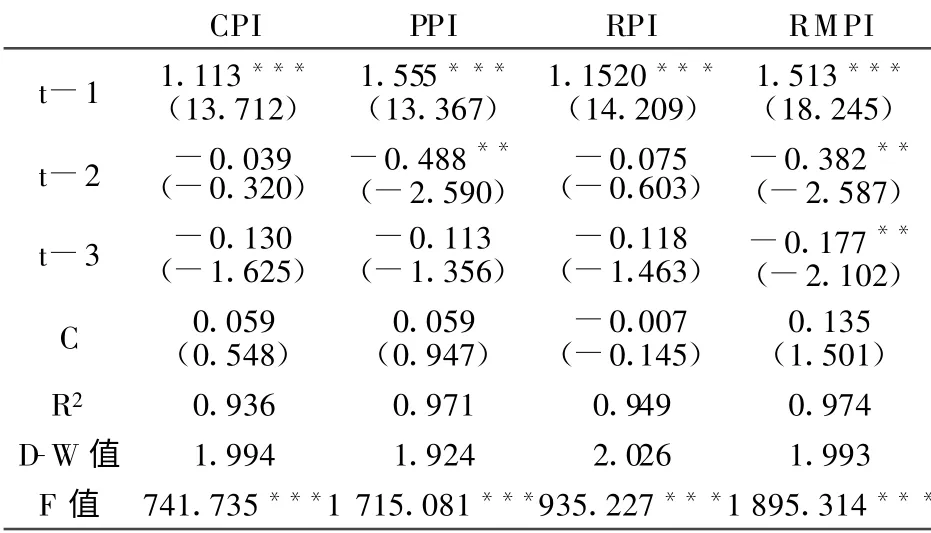
表1 物价自回归方程结果

(二)转移概率矩阵的计算

由于CPI、PPI、RPI和RMPI四个指标中,只有CPI和RPI的变化过程具有马尔可夫性质,因此本文主要分析CPI和RPI的变化趋势。在计算CPI和RPI的转移概率矩阵前,需要对CPI和RPI进行状态划分,本文将CPI和RPI划分为6个状态{S1,S2,S3,S4,S5,S6},具体见表2。根据表2和图1可以发现:从1997年1月到现在,CPI的波动趋势大多数处在状态S3,其次是处于状态S2,而RPI的波动趋势大多数处在状态S2,其次是处于S3。从图1还可以发现:从1997年1月到现在,大部分时间都是CPI曲线处于RP曲线上面,即消费者价格指数同比增长率高于商品零售价格指数同比增长率。

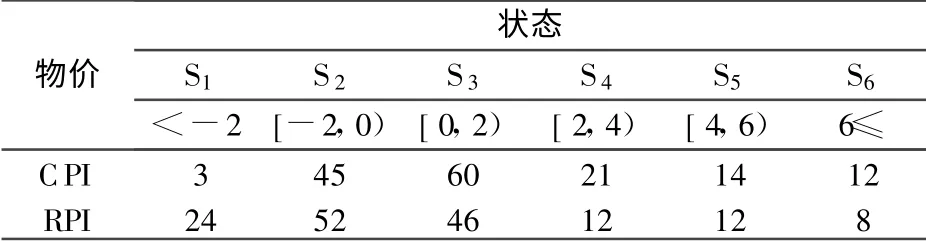
表2 CPI和RPI变化的状态划分

对于一步状态转移概率的计算,可以利用状态之间转移的频率作为该概率的估计值。假如在样本空间内状态S1出现的次数为m,由状态S1转移到状态S2的次数为n,则状态S1转移到状态S2的频率就近似为状态S1转移到状态S2的概率,即依次类推可以求出各个状态之间相互转移的概率。CPI和RPI的一步状态转移概率矩阵如下:解得CPI和RPI的一步状态转移概率矩阵后,就可以对CPI和RPI走势变化的持续性进行分析,同时还可以对CPI和RPI长期走势进行预测。

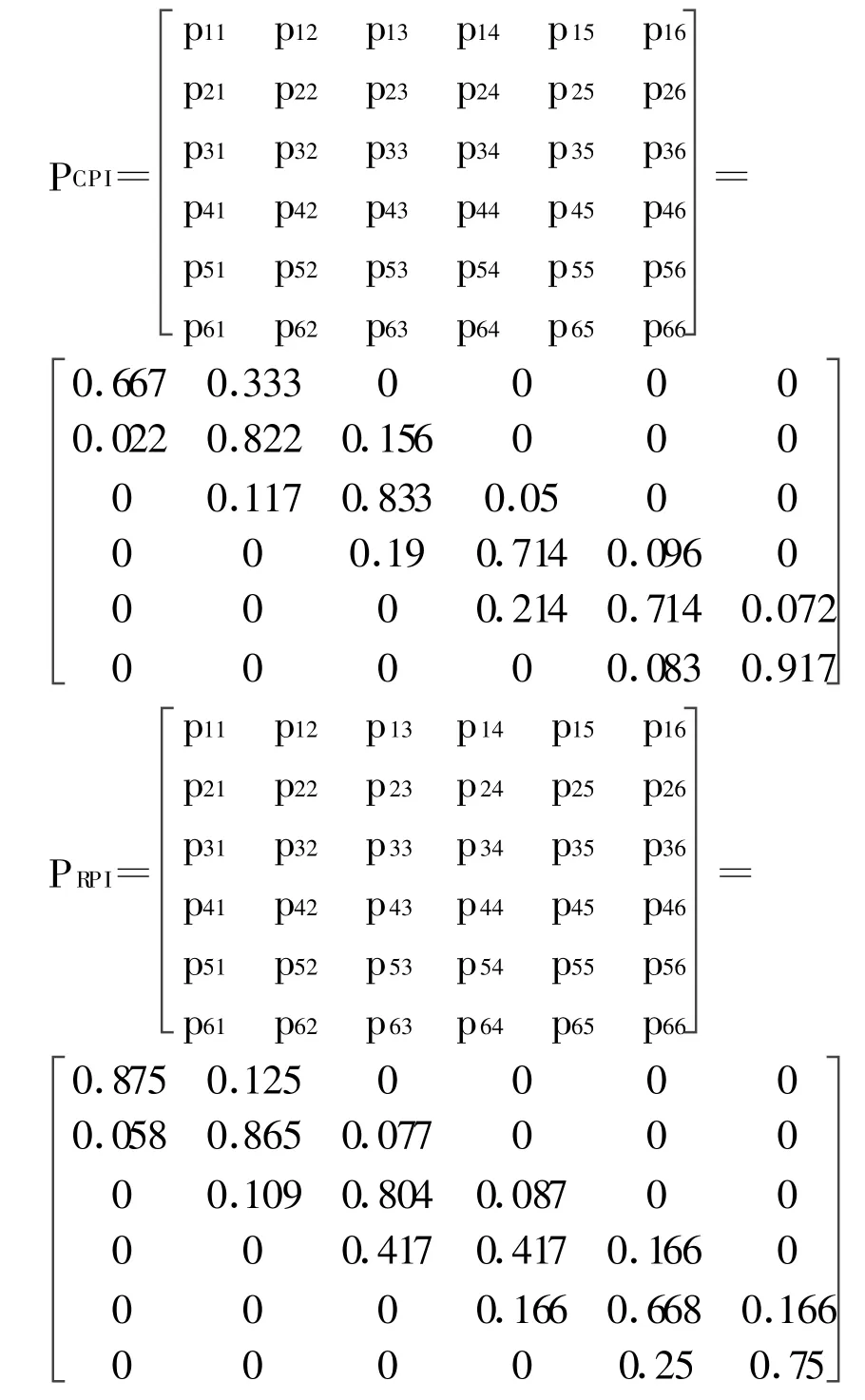
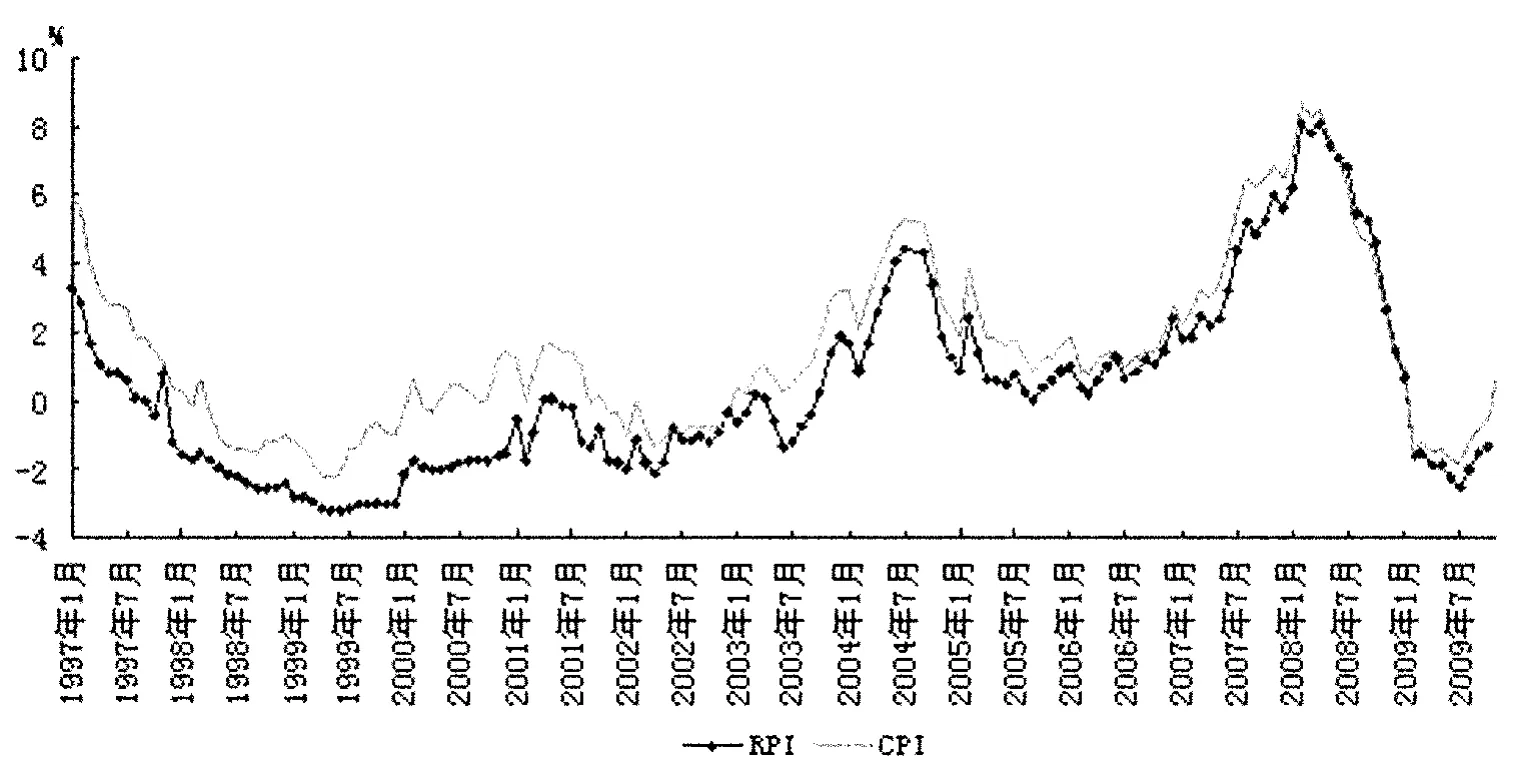
图1 CPI和RPI的波动趋势

(三)物价走势变化的持续性分析

持续性分析就是对时间序列变量处于某一状态的平均持续时间长度的研究。假设时间序列变量在tn+1时刻标志着状态Si的开始,这样的状态持续到tn+k时刻才结束,也就是说:Ztn+1=Ztn+2=…=Ztn+k=Si,Ztn+k+1=Sj。那么,时间序列变量处于状态Si持续时间的期望就可以写成[4]:

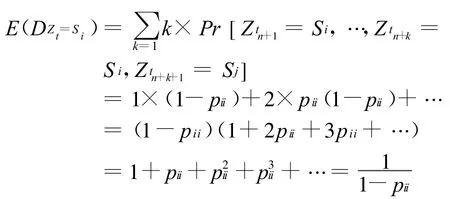
其中,pii表示时间序列Zt当期和下一期都处于状态Si的一步转移概率。根据CPI和RPI一步状态转移概率矩阵可以求出它们各状态的持续期,具体结果见表3和表4。

根据表3可以发现:CPI处于状态S6时有着较长的持续期,平均持续期是12个月左右,也就是说,当消费者价格指数增长率大于6%时,它在短期内很难降下来。根据图1也可以发现,2007年8月开始到2008年7月,连续12月消费者价格指数增长率大于6%,实证结果与实际情况相符合。另外,当CPI处于状态S1时有着较短的持续期,它平均只有3个月左右(见表3)。这表明,当消费者价格指数增长率小于-2%时,在短时间内又将上升。从图1中可以看到,1999年4月开始,消费者价格指数增长率小于-2%,但是这一状态只持续了3个月,到1999年7月开始消费者价格指数就开始上升了。根据表4可以发现:RPI处于状态S1和状态S2时有着较长的持续期,分别是8个月与7.4个月左右;RPI处于状态S4时有着较短的持续期,它平均只有1.7个月左右。这说明,商品零售价格指数增长率与消费者价格指数增长率不同,它在状态S6时没有较长的持续性,在状态S1和S2时有着较长的持续期。

(四)物价走势的预测

根据马尔可夫链模型的性质,可以把不同时期的状态概率用状态向量π(k)表示,其中π(k)=π(0)Pk。当时间趋于无穷时,由k步转移概率的平稳性质得到CPI和RPI最终的均衡分布向量π,即根据稳定条件方程组,就可以求出CPI和RPI的平稳状态概率值[5]。根据CPI和RPI的一步转移概率矩阵,运用MATLAB软件就可以分别解出CPI和RPI的平稳状态概率值,具体结果如下:

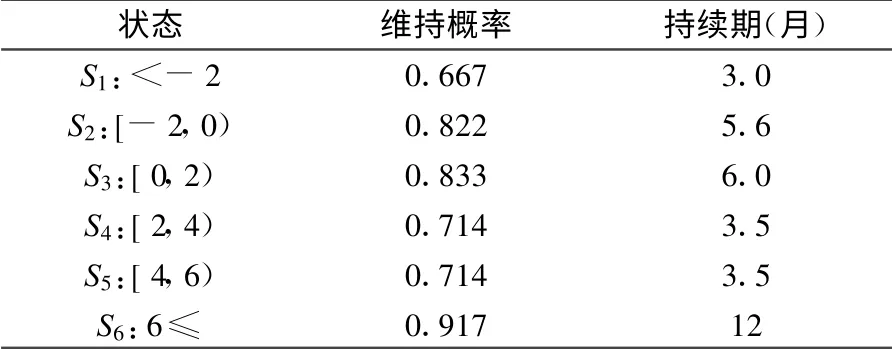
表3 CPI各状态的持续期

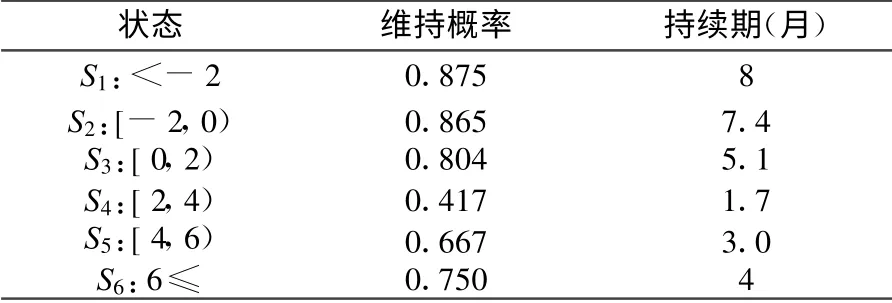
表4 RPI各状态的持续期

根据CPI的平稳状态概率值可以发现:消费者价格指数是2.18%的概率处于状态S1,32.89%的概率处于状态S2,43.84%的概率处于状态S3,11.52%的概率处于状态S4,5.15%的概率处于状态S5,4.42%的概率处于状态S6。这表明,长期来看未来消费者价格指数保持在状态S2(-2%≤CPI＜0)和状态S3(0≤CPI＜2%)的概率都是比较大的,其中保持在状态S3(0≤CPI＜2%)的概率最大,而它保持状态S6(6%≤CPI)的概率很小。

根据RPI的平稳状态概率值可以发现:商品零售价格指数是18.11%的概率处于状态S1,39.04%的概率处于状态S2,27.58%的概率处于状态S3,5.75%的概率处于状态S4,5.72%的概率处于状态S5,3.8%的概率处于状态S6。这表明,长期来看未来商品零售价格指数保持在状态S2(-2%≤RPI＜0)和状态S3(0≤RPI＜2%)的概率都是比较大的,其中保持在状态S2(-2%≤RPI＜0)的概率最大,而它保持状态S6(6%≤RPI)的概率最小。

四、结 论

在消费者价格指数(CPI)增长率、生产者价格指数(PPI)增长率、商品零售价格指数(RPI)增长率、原材料、燃料和动力购进价格指数(RMPI)增长率四个指标中,只有消费者价格指数(CPI)增长率和商品零售价格指数(RPI)增长率两个时间序列变量具有马尔可夫性质,所以本文主要分析CPI和RPI的变化趋势。以上研究结果表明:(1)当CPI增长率大于6%时,它就会具有一个较长的持续期,在短期内很难降下来,当消费者价格指数增长率小于-2%时,它的持续性较短,在短时间内又将上升。RPI与CPI相比则有所不同,当增长率大于6%时,它没有较长的持续性,它在状态S1(-4%≤CPI＜-2)和状态S2(-2%≤CPI＜0)时有着较长的持续期。(2)长期来看未来消费者价格指数保持在状态S2(-2%≤CPI＜0)和状态S3(0≤CPI＜2%)的概率都是比较大的,其中保持在状态S3(0≤CPI＜2%)的概率最大,而它保持状态S6(6%≤CPI)的概率很小。长期来看未来商品零售价格指数保持在状态S2(-2%≤RPI＜0)和状态S3(0≤RPI＜2%)的概率都是比较大的,其中保持在状态S2(-2%≤RPI＜0)的概率最大,而它保持状态S6(6%≤RPI)的概率很小。根据以上两点结果可以发现:对于CPI而言,虽然它保持状态S6(6%≤CPI)的概率很小,但是它一旦进入这个状态,就会具有一个较长的持续期,在短期内很难降下来;对于RPI而言,状态S2(-2%≤RPI＜0)是一个比较稳定的状态,同时在这状态时,它还具有较长的持续期。

注释:

①pij(tn-1,tn)也称为一步转移概率,而pij(tn-k,tn)称为k步转移概率,简记为pij(k)。

[1]陈乐一.辩证看物价涨落[N].中国经济时报,2008-06-27(5).

[2]彭湘君,余翔.入世后国际贸易与国内物价水平变动的实证研究[J].贵州财经学院学报,2008,(3):34-39.

[3]张桂喜.经济预测、决策与对策[M].北京:首都经济贸易大学出版社,2004.

[4]张成思.金融计量学——时间序列分析视角[M].大连:东北财经大学出版社,2008.

[5]李工农,阮晓青,徐晨.经济预测与决策及其Matlab实现[M].北京:清华大学出版社,2007.